2021-2022学年北师大版数学八上同步检测附答案1.1 探索勾股定理(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学八上同步检测附答案1.1 探索勾股定理(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 481.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 00:00:00 | ||
图片预览

文档简介
1.1
探索勾股定理
一、选择题(共10小题;共50分)
1.
下列各组数中不能作为直角三角形的三边长的是
A.
,,
B.
,,
C.
,,
D.
,,
2.
已知直角三角形两直角边的长为
和
,则该直角三角形的斜边的长度为
A.
B.
C.
D.
3.
直角三角形的两直角边分别为
,,则斜边上的高的长为
A.
B.
C.
D.
4.
若等腰三角形腰长为
,底边长为
,那么它的面积为
A.
B.
C.
D.
5.
如图所示,一棵大树在一次强台风中于离地面
米处折断倒下,倒下部分与地面成
夹角,这棵大树在折断前的高度为
A.
米
B.
米
C.
米
D.
米
6.
若一个直角三角形的一条直角边长是
,另一条直角边比斜边短
,则斜边长为
A.
B.
C.
D.
7.
在
中,,,,
分别是
,,
的对边.若
,,则
的面积为
A.
B.
C.
D.
8.
如图所示,一艘轮船以
海里/时的速度从港口
出发向东北方向航行,另一艘轮船以
海里/时的速度同时从港口
出发向东南方向航行,离开港口
小时后,两船相距
A.
海里
B.
海里
C.
海里
D.
海里
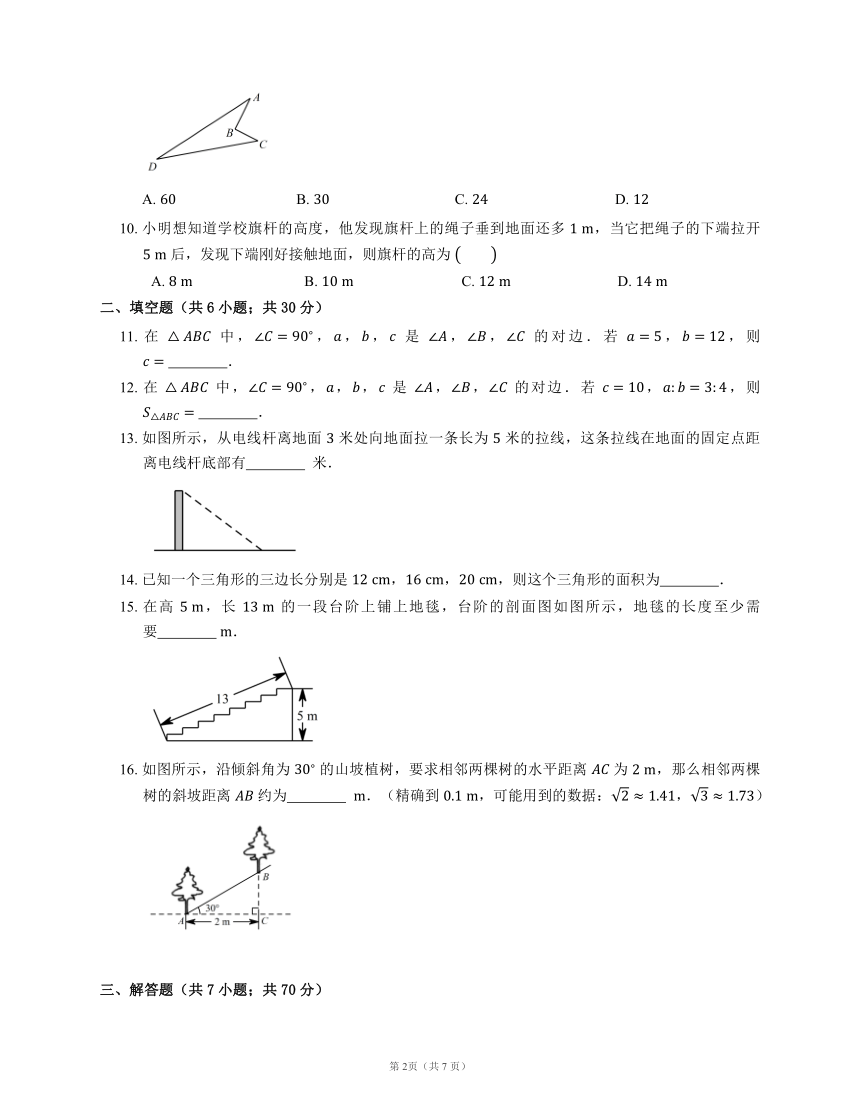
9.
一块木板如图所示,已知
,,,,,木板的面积为
A.
B.
C.
D.
10.
小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多
,当它把绳子的下端拉开
后,发现下端刚好接触地面,则旗杆的高为
A.
B.
C.
D.
二、填空题(共6小题;共30分)
11.
在
中,,,,
是
,,
的对边.若
,,则
?.
12.
在
中,,,,
是
,,
的对边.若
,,则
?.
13.
如图所示,从电线杆离地面
米处向地面拉一条长为
米的拉线,这条拉线在地面的固定点距离电线杆底部有
?
米.
14.
已知一个三角形的三边长分别是
,,,则这个三角形的面积为
?.
15.
在高
,长
的一段台阶上铺上地毯,台阶的剖面图如图所示,地毯的长度至少需要
?
.
16.
如图所示,沿倾斜角为
的山坡植树,要求相邻两棵树的水平距离
为
,那么相邻两棵树的斜坡距离
约为
?
.(精确到
,可能用到的数据:,)
三、解答题(共7小题;共70分)
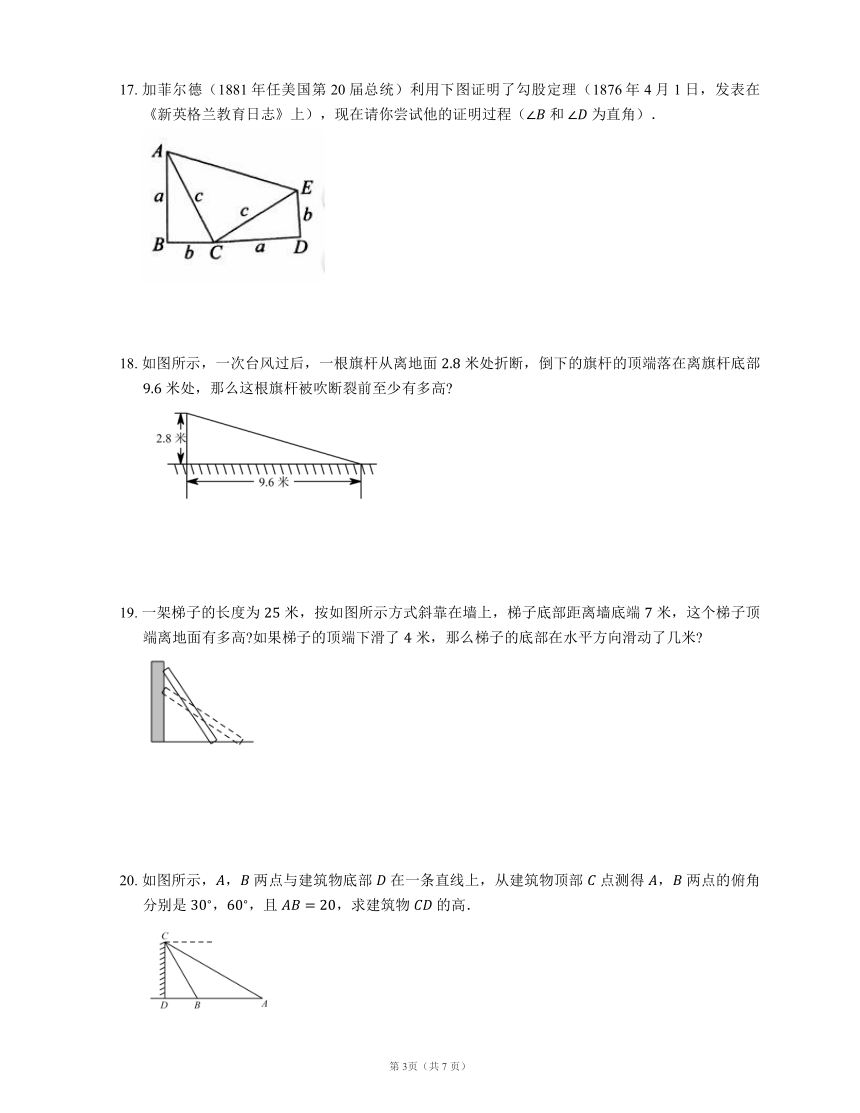
17.
加菲尔德(1881年任美国第20届总统)利用下图证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现在请你尝试他的证明过程(
和
为直角).
18.
如图所示,一次台风过后,一根旗杆从离地面
米处折断,倒下的旗杆的顶端落在离旗杆底部
米处,那么这根旗杆被吹断裂前至少有多高?
19.
一架梯子的长度为
米,按如图所示方式斜靠在墙上,梯子底部距离墙底端
米,这个梯子顶端离地面有多高?如果梯子的顶端下滑了
米,那么梯子的底部在水平方向滑动了几米?
20.
如图所示,,
两点与建筑物底部
在一条直线上,从建筑物顶部
点测得
,
两点的俯角分别是
,,且
,求建筑物
的高.
21.
如图所示,海中有一小岛
,在该岛周围
海里内有暗礁.今有货船由西向东航行,开始在
岛南偏西
的
处,往东航行
海里后,到达该岛南偏西
的
处,之后继续向东航行.你认为货船继续向东航行,会有触礁的危险吗?计算后说明理由.
22.
如图所示,长方体的长为
,宽为
,高为
,点
与点
之间相距
,
一只蚂蚁如果要沿着长方体的表面从点
爬到点
,需要爬行的最短距离是多少?
23.
如图所示,有一块直角三角形纸片,两直角边
,,现将直角边
沿直线
折叠,使它恰好落在斜边
上,且与
重合,求
的长.
答案
1.
A
2.
D
3.
D
4.
A
5.
B
6.
D
7.
A
8.
D
9.
C
【解析】提示:连接
.
10.
C
【解析】设旗杆的高为
,则绳子的长为
,
有题意可得:,
解得:,即旗杆的高是
.
11.
12.
13.
14.
15.
16.
【解析】,
,
.
17.
,,
的面积和等于梯形
的面积.
18.
如图:斜边长
.
旗杆的高为
米.
答:这根旗杆被吹断裂前至少有
米.
19.
由题意可知:梯子的高度
(米).
设梯子的顶端下滑了
米,那么梯子的底部在水平方向滑动了
米.
则
.
解得
.
梯子的顶端下滑了
米,那么梯子的底部在水平方向滑动了
米.
20.
由题意可知
,,
,
.
.
.
,
.
.
答:建筑物
的高是
.
21.
不会.
作
于点
.
,,
.
又
,
.
.
.
22.
.
23.
.
第1页(共7
页)
探索勾股定理
一、选择题(共10小题;共50分)
1.
下列各组数中不能作为直角三角形的三边长的是
A.
,,
B.
,,
C.
,,
D.
,,
2.
已知直角三角形两直角边的长为
和
,则该直角三角形的斜边的长度为
A.
B.
C.
D.
3.
直角三角形的两直角边分别为
,,则斜边上的高的长为
A.
B.
C.
D.
4.
若等腰三角形腰长为
,底边长为
,那么它的面积为
A.
B.
C.
D.
5.
如图所示,一棵大树在一次强台风中于离地面
米处折断倒下,倒下部分与地面成
夹角,这棵大树在折断前的高度为
A.
米
B.
米
C.
米
D.
米
6.
若一个直角三角形的一条直角边长是
,另一条直角边比斜边短
,则斜边长为
A.
B.
C.
D.
7.
在
中,,,,
分别是
,,
的对边.若
,,则
的面积为
A.
B.
C.
D.
8.
如图所示,一艘轮船以
海里/时的速度从港口
出发向东北方向航行,另一艘轮船以
海里/时的速度同时从港口
出发向东南方向航行,离开港口
小时后,两船相距
A.
海里
B.
海里
C.
海里
D.
海里
9.
一块木板如图所示,已知
,,,,,木板的面积为
A.
B.
C.
D.
10.
小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多
,当它把绳子的下端拉开
后,发现下端刚好接触地面,则旗杆的高为
A.
B.
C.
D.
二、填空题(共6小题;共30分)
11.
在
中,,,,
是
,,
的对边.若
,,则
?.
12.
在
中,,,,
是
,,
的对边.若
,,则
?.
13.
如图所示,从电线杆离地面
米处向地面拉一条长为
米的拉线,这条拉线在地面的固定点距离电线杆底部有
?
米.
14.
已知一个三角形的三边长分别是
,,,则这个三角形的面积为
?.
15.
在高
,长
的一段台阶上铺上地毯,台阶的剖面图如图所示,地毯的长度至少需要
?
.
16.
如图所示,沿倾斜角为
的山坡植树,要求相邻两棵树的水平距离
为
,那么相邻两棵树的斜坡距离
约为
?
.(精确到
,可能用到的数据:,)
三、解答题(共7小题;共70分)
17.
加菲尔德(1881年任美国第20届总统)利用下图证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现在请你尝试他的证明过程(
和
为直角).
18.
如图所示,一次台风过后,一根旗杆从离地面
米处折断,倒下的旗杆的顶端落在离旗杆底部
米处,那么这根旗杆被吹断裂前至少有多高?
19.
一架梯子的长度为
米,按如图所示方式斜靠在墙上,梯子底部距离墙底端
米,这个梯子顶端离地面有多高?如果梯子的顶端下滑了
米,那么梯子的底部在水平方向滑动了几米?
20.
如图所示,,
两点与建筑物底部
在一条直线上,从建筑物顶部
点测得
,
两点的俯角分别是
,,且
,求建筑物
的高.
21.
如图所示,海中有一小岛
,在该岛周围
海里内有暗礁.今有货船由西向东航行,开始在
岛南偏西
的
处,往东航行
海里后,到达该岛南偏西
的
处,之后继续向东航行.你认为货船继续向东航行,会有触礁的危险吗?计算后说明理由.
22.
如图所示,长方体的长为
,宽为
,高为
,点
与点
之间相距
,
一只蚂蚁如果要沿着长方体的表面从点
爬到点
,需要爬行的最短距离是多少?
23.
如图所示,有一块直角三角形纸片,两直角边
,,现将直角边
沿直线
折叠,使它恰好落在斜边
上,且与
重合,求
的长.
答案
1.
A
2.
D
3.
D
4.
A
5.
B
6.
D
7.
A
8.
D
9.
C
【解析】提示:连接
.
10.
C
【解析】设旗杆的高为
,则绳子的长为
,
有题意可得:,
解得:,即旗杆的高是
.
11.
12.
13.
14.
15.
16.
【解析】,
,
.
17.
,,
的面积和等于梯形
的面积.
18.
如图:斜边长
.
旗杆的高为
米.
答:这根旗杆被吹断裂前至少有
米.
19.
由题意可知:梯子的高度
(米).
设梯子的顶端下滑了
米,那么梯子的底部在水平方向滑动了
米.
则
.
解得
.
梯子的顶端下滑了
米,那么梯子的底部在水平方向滑动了
米.
20.
由题意可知
,,
,
.
.
.
,
.
.
答:建筑物
的高是
.
21.
不会.
作
于点
.
,,
.
又
,
.
.
.
22.
.
23.
.
第1页(共7
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
