2.1 认识分式 课件(共42张PPT)
文档属性
| 名称 | 2.1 认识分式 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 21:06:33 | ||
图片预览











文档简介
第二章 分式与分式方程
1 认识分式
知识点一 分式的概念
分式满足的条件:
(1)形如????????的式子;
(2)A,B都是整式;
(3)分母B中含有字母,三者缺一不可.
?
知识点一 分式的概念
分式满足的条件:
(1)形如????????的式子;
(2)A,B都是整式;
(3)分母B中含有字母,三者缺一不可.
特别提醒
判断式子是不是分式要看原始形式,而不是看化简后的结果,如????????????是分式,而不是整式.
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
分析 分式和整式的区别是看分母中是否含有字母.
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
分析 分式和整式的区别是看分母中是否含有字母.
解析 整式: ????????,?????????????,???????? .
分式: ????????,????????+?????????????,????????? .
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
分析 分式和整式的区别是看分母中是否含有字母.
解析 整式: ????????,?????????????,???????? .
分式: ????????,????????+?????????????,????????? .
点拨 (1)区分整式与分式的关键是看分母,分母中含有字母的是分式,不含字母的是整式;(2)π是一个常数,所以是整式而不是分式.
?
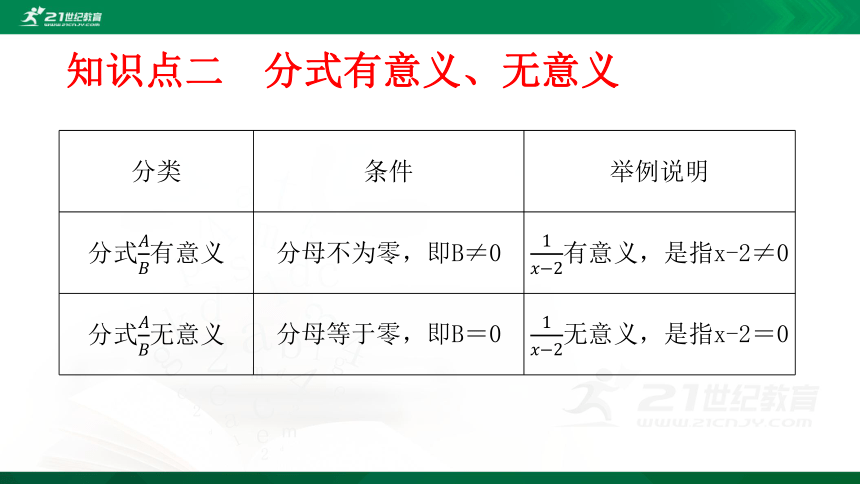
知识点二 分式有意义、无意义
分类
条件
举例说明
分式????????有意义
分母不为零,即B≠0
1?????2有意义,是指x-2≠0
分式????????无意义
分母等于零,即B=0
1?????2无意义,是指x-2=0
分类
条件
举例说明
分母不为零,即B≠0
分母等于零,即B=0
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
?
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
解析 因为代数式????+?????????????有意义,所以x-7≠0,所以x≠7.
?
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
解析 因为代数式????+?????????????有意义,所以x-7≠0,所以x≠7.
答案 x≠7
?
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
解析 因为代数式????+?????????????有意义,所以x-7≠0,所以x≠7.
答案 x≠7
点拨 分式有、无意义只与分母有关,与分子没有关系.
?
知识点三 分式值为零的条件
分式值为零的条件:
当分式的分子等于零,且分母不等于零时,分式的值为零
知识点三 分式值为零的条件
分式值为零的条件:
当分式的分子等于零,且分母不等于零时,分式的值为零
温馨提示:
分式的值是在分式有意义的前提下考虑的,所以使分式?????????=0的条件是A=0且B≠0,两者缺一不可.
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
解析 由题意得?????????=????????????+????≠?????,解得x=3.
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
解析 由题意得?????????=????????????+????≠?????,解得x=3.
答案 3
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
解析 由题意得?????????=????????????+????≠?????,解得x=3.
答案 3
点拨 解决此类问题的步骤:
(1)求出使分子为零的字母的值;
(2)检验这个字母的值是否使分母的值为零;
(3)使分母不为零的值就是所要求的字母的值.
?
知识点四 分式的基本性质
1.分式的基本性质
分式的分子与分母同乘(或除以)一个不等于零的整式,分式的值不变
字母表示 ????????=????×????????×????,????????=????÷????????÷????(M是不等于零的整式)
?
知识点四 分式的基本性质
1.分式的基本性质
分式的分子与分母同乘(或除以)一个不等于零的整式,分式的值不变
字母表示 ????????=????×????????×????,????????=????÷????????÷????(M是不等于零的整式)
2.分式的符号法则
分式的分子、分母与分式本身的符号,同时改变其中两个,分式的值不变
字母表示 ????????=??????????=??????????=??????????
?
例4 写出下列等式中未知的分子或分母.
(1)?????????????????=(??????????)???????????????????????; (2)????????????????????(????+????)=????(????????????????)
?
例4 写出下列等式中未知的分子或分母.
(1)?????????????????=(??????????)???????????????????????; (2)????????????????????(????+????)=????(????????????????)
解析 (1)观察分母,等号左边分式的分母是x-2y,等号右边分式的分母是x2-4y2,显然,x2-4y2是由(x-2y)乘(x+2y)得到的,由分式的基本性质知,等号左边分式的分子也要乘(x+2y),变为(x+2y).
(2)观察分子,等号左边分式的分子是a2b,等号右边分式的分子是a,显然是约去了因式ab,由分式的基本性质知,等式左边的分母也应约去因式ab,变为(a+b).
?
答案 (1)x+2y (2)a+b
答案 (1)x+2y (2)a+b
方法归纳
解有关分式恒等变形的填空题,一般地,先从分子或分母的已知项入手,观察变化方式,再把未知项进行相应的变形.
知识点五 分式的约分和最简分式
约分:
找公因式的方法:
最简分式:
知识点五 分式的约分和最简分式
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分,即????·????????·????=????????.
找公因式的方法:
最简分式:
?
知识点五 分式的约分和最简分式
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分,即????·????????·????=????????.
找公因式的方法:如果分式的分子、分母都是单项式,那么直接约去分子、分母中的公因式;如果分式的分子、分母中至少有一个多项式,那么先分解因式,再约去分子、分母的公因式.
最简分式:
?
知识点五 分式的约分和最简分式
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分,即????·????????·????=????????.
找公因式的方法:如果分式的分子、分母都是单项式,那么直接约去分子、分母中的公因式;如果分式的分子、分母中至少有一个多项式,那么先分解因式,再约去分子、分母的公因式.
最简分式:分子与分母没有公因式的分式叫做最简分式.
?
经典例题
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
?
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
分析 (1)分子与分母同时乘100;(2)分子与分母同时乘30.
?
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
分析 (1)分子与分母同时乘100;(2)分子与分母同时乘30.
解析 (1)????.?????????????????.????????????.?????????????????.????????=(????.?????????????????.????????)×????????????(????.?????????????????.????????)×????????????=???????????????????????????????????????????.
(2) ????????+?????????????????????????????????=????????+????????×?????????????????????????????????×????????=????????????+??????????????????????????????????????.
?
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
分析 (1)分子与分母同时乘100;(2)分子与分母同时乘30.
解析 (1)????.?????????????????.????????????.?????????????????.????????=(????.?????????????????.????????)×????????????(????.?????????????????.????????)×????????????=???????????????????????????????????????????.
(2) ????????+?????????????????????????????????=????????+????????×?????????????????????????????????×????????=????????????+??????????????????????????????????????.
点拨 解决此类问题的关键是确定分子、分母所乘的公倍数,只需将分式的分子、分母同时乘公倍数,就可以将分式的分子与分母中各项的系数化为整数,且使这个分式的值不变.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
分析 先把分子、分母分解因式,约分化简,再代入求值.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
分析 先把分子、分母分解因式,约分化简,再代入求值.
解析 ??????????????????????????????????=????(?????????)(?????????)(????+????)=?????????+?????.
当a=-3,b=2时,原式=???????????+????=??????.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
分析 先把分子、分母分解因式,约分化简,再代入求值.
解析 ??????????????????????????????????=????(?????????)(?????????)(????+????)=?????????+?????.
当a=-3,b=2时,原式=???????????+????=??????.
点拨 化简求值题一定要先把分式化成最简分式或整式,再代入求值.
?
易错易混
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
?
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
分析 根据分式值为零满足的条件“分子等于零且分母不等于零”,列出方程和不等式求解.
?
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
分析 根据分式值为零满足的条件“分子等于零且分母不等于零”,列出方程和不等式求解.
解析 根据题意得????????+????=?????????????????≠????,所以x=0.
?
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
分析 根据分式值为零满足的条件“分子等于零且分母不等于零”,列出方程和不等式求解.
解析 根据题意得????????+????=?????????????????≠????,所以x=0.
易错警示 分式的值为零必须同时满足两个条件:分子等于零且分母不等于零分式的分母不为零时,分式才有意义,在解题过程中不能忽略“分母不等于零”这一条件.
1 认识分式
知识点一 分式的概念
分式满足的条件:
(1)形如????????的式子;
(2)A,B都是整式;
(3)分母B中含有字母,三者缺一不可.
?
知识点一 分式的概念
分式满足的条件:
(1)形如????????的式子;
(2)A,B都是整式;
(3)分母B中含有字母,三者缺一不可.
特别提醒
判断式子是不是分式要看原始形式,而不是看化简后的结果,如????????????是分式,而不是整式.
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
分析 分式和整式的区别是看分母中是否含有字母.
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
分析 分式和整式的区别是看分母中是否含有字母.
解析 整式: ????????,?????????????,???????? .
分式: ????????,????????+?????????????,????????? .
?
例1 下列各式中,哪些是整式?哪些是分式?
????????,????????,????????+?????????????,?????????,?????????????,?????????.
分析 分式和整式的区别是看分母中是否含有字母.
解析 整式: ????????,?????????????,???????? .
分式: ????????,????????+?????????????,????????? .
点拨 (1)区分整式与分式的关键是看分母,分母中含有字母的是分式,不含字母的是整式;(2)π是一个常数,所以是整式而不是分式.
?
知识点二 分式有意义、无意义
分类
条件
举例说明
分式????????有意义
分母不为零,即B≠0
1?????2有意义,是指x-2≠0
分式????????无意义
分母等于零,即B=0
1?????2无意义,是指x-2=0
分类
条件
举例说明
分母不为零,即B≠0
分母等于零,即B=0
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
?
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
解析 因为代数式????+?????????????有意义,所以x-7≠0,所以x≠7.
?
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
解析 因为代数式????+?????????????有意义,所以x-7≠0,所以x≠7.
答案 x≠7
?
知识点二 分式有意义、无意义
例2 若代数式????+?????????????有意义,则实数x的取值范围是_________.
解析 因为代数式????+?????????????有意义,所以x-7≠0,所以x≠7.
答案 x≠7
点拨 分式有、无意义只与分母有关,与分子没有关系.
?
知识点三 分式值为零的条件
分式值为零的条件:
当分式的分子等于零,且分母不等于零时,分式的值为零
知识点三 分式值为零的条件
分式值为零的条件:
当分式的分子等于零,且分母不等于零时,分式的值为零
温馨提示:
分式的值是在分式有意义的前提下考虑的,所以使分式?????????=0的条件是A=0且B≠0,两者缺一不可.
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
解析 由题意得?????????=????????????+????≠?????,解得x=3.
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
解析 由题意得?????????=????????????+????≠?????,解得x=3.
答案 3
?
例3 对于分式?????????????????+????,当x=_______时,分式的值为零.
解析 由题意得?????????=????????????+????≠?????,解得x=3.
答案 3
点拨 解决此类问题的步骤:
(1)求出使分子为零的字母的值;
(2)检验这个字母的值是否使分母的值为零;
(3)使分母不为零的值就是所要求的字母的值.
?
知识点四 分式的基本性质
1.分式的基本性质
分式的分子与分母同乘(或除以)一个不等于零的整式,分式的值不变
字母表示 ????????=????×????????×????,????????=????÷????????÷????(M是不等于零的整式)
?
知识点四 分式的基本性质
1.分式的基本性质
分式的分子与分母同乘(或除以)一个不等于零的整式,分式的值不变
字母表示 ????????=????×????????×????,????????=????÷????????÷????(M是不等于零的整式)
2.分式的符号法则
分式的分子、分母与分式本身的符号,同时改变其中两个,分式的值不变
字母表示 ????????=??????????=??????????=??????????
?
例4 写出下列等式中未知的分子或分母.
(1)?????????????????=(??????????)???????????????????????; (2)????????????????????(????+????)=????(????????????????)
?
例4 写出下列等式中未知的分子或分母.
(1)?????????????????=(??????????)???????????????????????; (2)????????????????????(????+????)=????(????????????????)
解析 (1)观察分母,等号左边分式的分母是x-2y,等号右边分式的分母是x2-4y2,显然,x2-4y2是由(x-2y)乘(x+2y)得到的,由分式的基本性质知,等号左边分式的分子也要乘(x+2y),变为(x+2y).
(2)观察分子,等号左边分式的分子是a2b,等号右边分式的分子是a,显然是约去了因式ab,由分式的基本性质知,等式左边的分母也应约去因式ab,变为(a+b).
?
答案 (1)x+2y (2)a+b
答案 (1)x+2y (2)a+b
方法归纳
解有关分式恒等变形的填空题,一般地,先从分子或分母的已知项入手,观察变化方式,再把未知项进行相应的变形.
知识点五 分式的约分和最简分式
约分:
找公因式的方法:
最简分式:
知识点五 分式的约分和最简分式
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分,即????·????????·????=????????.
找公因式的方法:
最简分式:
?
知识点五 分式的约分和最简分式
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分,即????·????????·????=????????.
找公因式的方法:如果分式的分子、分母都是单项式,那么直接约去分子、分母中的公因式;如果分式的分子、分母中至少有一个多项式,那么先分解因式,再约去分子、分母的公因式.
最简分式:
?
知识点五 分式的约分和最简分式
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分,即????·????????·????=????????.
找公因式的方法:如果分式的分子、分母都是单项式,那么直接约去分子、分母中的公因式;如果分式的分子、分母中至少有一个多项式,那么先分解因式,再约去分子、分母的公因式.
最简分式:分子与分母没有公因式的分式叫做最简分式.
?
经典例题
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
?
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
分析 (1)分子与分母同时乘100;(2)分子与分母同时乘30.
?
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
分析 (1)分子与分母同时乘100;(2)分子与分母同时乘30.
解析 (1)????.?????????????????.????????????.?????????????????.????????=(????.?????????????????.????????)×????????????(????.?????????????????.????????)×????????????=???????????????????????????????????????????.
(2) ????????+?????????????????????????????????=????????+????????×?????????????????????????????????×????????=????????????+??????????????????????????????????????.
?
题型一 分式的基本性质的应用
例1 不改变分式的值,将下列分式的分子与分母中的各项系数化为整数.
(1)????.?????????????????.????????????.?????????????????.????????;(2)????????+????????????????????????????????? .
分析 (1)分子与分母同时乘100;(2)分子与分母同时乘30.
解析 (1)????.?????????????????.????????????.?????????????????.????????=(????.?????????????????.????????)×????????????(????.?????????????????.????????)×????????????=???????????????????????????????????????????.
(2) ????????+?????????????????????????????????=????????+????????×?????????????????????????????????×????????=????????????+??????????????????????????????????????.
点拨 解决此类问题的关键是确定分子、分母所乘的公倍数,只需将分式的分子、分母同时乘公倍数,就可以将分式的分子与分母中各项的系数化为整数,且使这个分式的值不变.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
分析 先把分子、分母分解因式,约分化简,再代入求值.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
分析 先把分子、分母分解因式,约分化简,再代入求值.
解析 ??????????????????????????????????=????(?????????)(?????????)(????+????)=?????????+?????.
当a=-3,b=2时,原式=???????????+????=??????.
?
题型二 分式的化简求值
例2 先化简,再求分式??????????????????????????????????的值,其中a=-3,b=2.
分析 先把分子、分母分解因式,约分化简,再代入求值.
解析 ??????????????????????????????????=????(?????????)(?????????)(????+????)=?????????+?????.
当a=-3,b=2时,原式=???????????+????=??????.
点拨 化简求值题一定要先把分式化成最简分式或整式,再代入求值.
?
易错易混
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
?
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
分析 根据分式值为零满足的条件“分子等于零且分母不等于零”,列出方程和不等式求解.
?
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
分析 根据分式值为零满足的条件“分子等于零且分母不等于零”,列出方程和不等式求解.
解析 根据题意得????????+????=?????????????????≠????,所以x=0.
?
易错点 忽视分式有意义时需满足的条件
例 当x为何值时,????(?????????)?????????????的值等于零?
分析 根据分式值为零满足的条件“分子等于零且分母不等于零”,列出方程和不等式求解.
解析 根据题意得????????+????=?????????????????≠????,所以x=0.
易错警示 分式的值为零必须同时满足两个条件:分子等于零且分母不等于零分式的分母不为零时,分式才有意义,在解题过程中不能忽略“分母不等于零”这一条件.
