2021-2022学年沪教新版九年级上册数学《第24章 相似三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版九年级上册数学《第24章 相似三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 566.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 05:30:25 | ||
图片预览

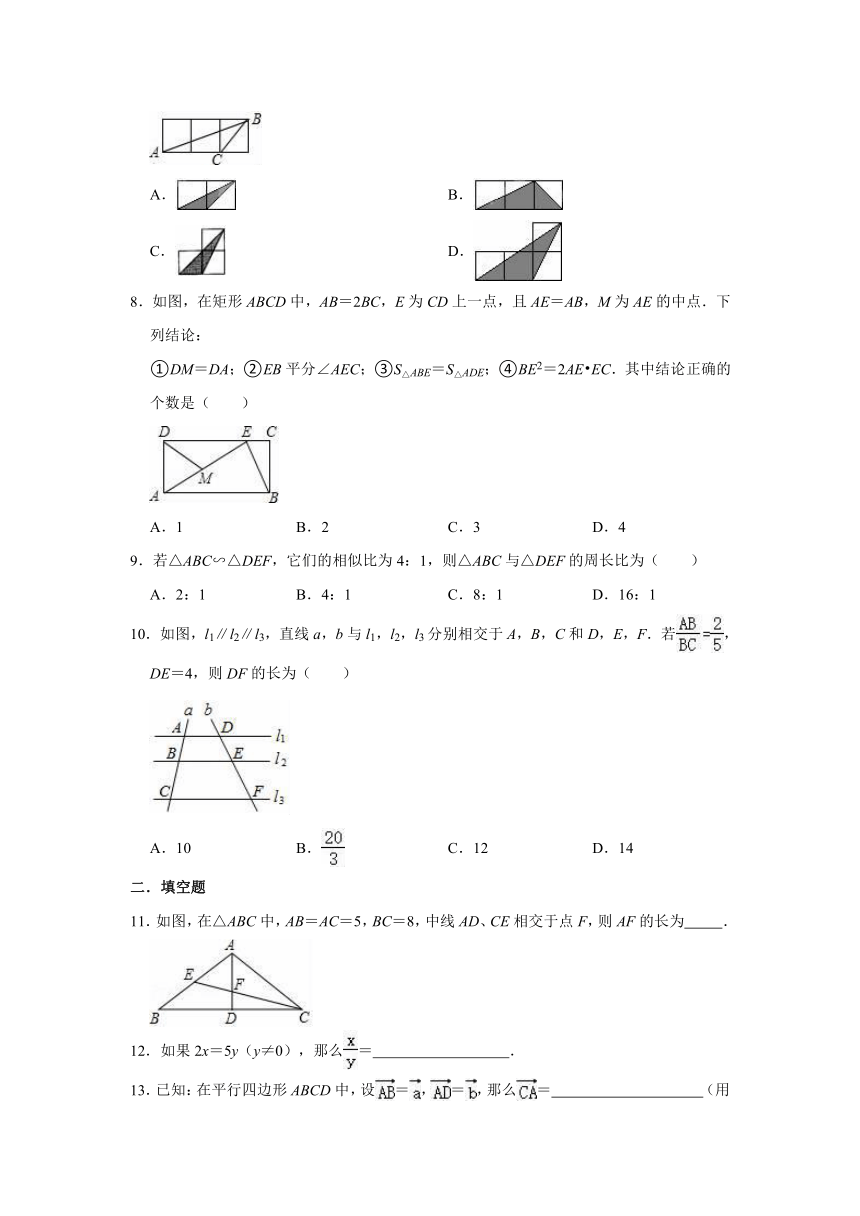


文档简介
2021-2022学年沪教新版九年级上册数学《第24章
相似三角形》单元测试卷
一.选择题
1.如果是非零向量,那么下列等式正确的是( )
A.=
B.=
C.
+=0
D.
+=0
2.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长为( )
A.3cm
B.4
cm
C.5cm
D.6
cm
3.已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为( )
A.
B.
C.
D.
4.下列图形中,一定相似的是( )
A.两个矩形
B.有一组角相等的两个等腰三角形
C.有一组对应角相等的两个菱形
D.两边对应成比例且有一组角相等的三角形
5.已知3a=2b(a≠0,b≠0),下列变形错误的是( )
A.
B.
C.
D.
6.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①;②;③;④,其中正确的结论是有( )个.
A.1
B.2
C.3
D.4
7.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A.
B.
C.
D.
8.如图,在矩形ABCD中,AB=2BC,E为CD上一点,且AE=AB,M为AE的中点.下列结论:
①DM=DA;②EB平分∠AEC;③S△ABE=S△ADE;④BE2=2AE?EC.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
9.若△ABC∽△DEF,它们的相似比为4:1,则△ABC与△DEF的周长比为( )
A.2:1
B.4:1
C.8:1
D.16:1
10.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为( )
A.10
B.
C.12
D.14
二.填空题
11.如图,在△ABC中,AB=AC=5,BC=8,中线AD、CE相交于点F,则AF的长为
.
12.如果2x=5y(y≠0),那么=
.
13.已知:在平行四边形ABCD中,设=,=,那么=
(用向量、的式子表示).
14.已知点P是线段AB的黄金分割点,AP>PB.若AB=2,则AP=
.
15.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=
.
16.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为
cm.
17.如图,∠1=∠2,添加一个条件使得△ADE∽△ACB,可添加的条件是
.
18.在比例尺为1:30000的地图上,量得A、B两地的图上距离AB=5cm,则A、B两地的实际距离为
km.
19.如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC=,AD=CD=,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于
.
20.如图,在等腰Rt△ABC中,AC=BC=6,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若=,则AH的长为
.
三.解答题
21.已知P为线段AB上一点,且AB被点P分为AP:PB=2:3.
(1)求AB:BP;
(2)如果AB=100cm,试求PB的长.
22.如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α﹣β|,于是|α﹣β|越小,菱形越接近正方形.
①若菱形的一个内角为80°,则该菱形的“接近度”为
;
②当菱形的“接近度”等于
时,菱形是正方形;
(2)设矩形的长和宽分别为m,n(m≤n),试写出矩形的“接近度”的合理定义.
23.如图,已知AD是△ABC的中线,G是重心.
(1)设=,=,用向量、表示;
(2)如果AB=3,AC=2,∠GAC=∠GCA,求BG的长.
24.若,且2a﹣b+3c=21.试求a:b:c.
25.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
26.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD=2BD,已知,.
(1)用向量、分别表示向量、;
(2)作出向量分别在、方向上的分向量(写出结论,不要求写作法).
27.如图,△ABC中,AB=AC,∠A=36°,CE平分∠ACB交AB于点E,
(1)试说明点E为线段AB的黄金分割点;
(2)若AB=4,求BC的长.
参考答案与试题解析
一.选择题
1.解:∵是非零向量,
∴||=||.
故选:A.
2.解:已知a,b,c,d是成比例线段,
根据比例线段的定义得:ad=cb,
代入a=3cm,b=2cm,c=6cm,
解得:d=4,
则d=4cm.
故选:B.
3.解:根据题意得AP=AB,
所以PB=AB﹣AP=AB,
所以PB:AB=.
故选:B.
4.解:A、两个矩形对应边的比值不一定相等,故此选项错误;
B、有一组角相等的两个等腰三角形,有可能是两三角形的底角与顶角对应相等,故此选项错误;
C、有一组对应角相等的两个菱形,相似,故此选项正确;
D、两边对应成比例且两边的夹角相等的三角形相似,故此选项错误.
故选:C.
5.解:A、∵3a=2b,
∴两边都除以3b得:=,故本选项不符合题意;
B、∵3a=2b,
∴两边都除以2a得:=,故本选项符合题意;
C、3a=2b,
∴两边都除以2a得:=,故本选项不符合题意;
D、∵3a=2b,
∴两边都除以6得:=,故本选项不符合题意;
故选:B.
6.解:∵AD=DB,AE=EC,
∴DE∥BC,DE:BC=1:2,
∴==,故①③正确,
设S△DOE=S,则S△EOC=2S,S△BOC=4s,
∴=,故②错误,
∵DE∥BC,
∴=1,故④错误,
故选:B.
7.解:根据题意得:AB==,AC=2,BC==,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
8.解:①∵在直角△ADE中,∠ADE=90°,M为AE的中点,∴DM=AE,∵AE=AB,AB=2BC=2DA,∴DM=DA,正确;
②在直角△ADE中,∠ADE=90°,AD=AE,∴∠DEA=30°.∵CD∥AB,∴∠EAB=∠DEA=30°,∠CEB=∠ABE.在△EAB中,∠EAB=30°,AE=AB,∴∠AEB=∠ABE=75°,∴∠CEB=75°,∴EB平分∠AEC,正确;
③∵S△ABE=S矩形ABCD,S△ADE<S△ADC=S矩形ABCD,∴S△ABE>S△ADE,错误;
④在矩形ABCD中,设BC=DA=a,则AE=AB=DC=2BC=2a,DE=AD=a,∴EC=(2﹣)a.在直角△BCE中,BE2=BC2+CE2=a2+[(2﹣)a]2=(8﹣4)a2,2AE?EC=2×2a×(2﹣)a=(8﹣4)a2,正确.
故选:C.
9.解:∵△ABC∽△DEF,它们的相似比为4:1,
∴△ABC与△DEF的周长的比为:4:1.
故选:B.
10.解:∵l1∥l2∥l3,
∴==,
∵DE=4,
∴EF=10,
∴DF=DE+EF=4+10=14,
故选:D.
二.填空题
11.解:∵AB=AC,AD为中线,
∴AD⊥BC,BD=CD=BC=4,
在Rt△ABD中,AD==3,
∵点F为中线AD、CE的交点,
∴F点为△ABC的重心,
∴AF=AD=×3=2.
故答案为2.
12.解:∵2x=5y(y≠0),
∴=.
故答案为:.
13.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴==,
∵=,
∴=﹣,=﹣,
∴=+=﹣﹣.
故答案为:﹣﹣.
14.解:由于P为线段AB=2的黄金分割点,
且AP是较长线段;
则AP=2×=﹣1.
15.解:∵线段AD、BE是△ABC的中线,
∴=,=,
∵EF∥BC,=,
∴=.
故答案为:.
16.解:∵△ABC∽△A′B′C′,且,即相似三角形的相似比是
∵△ABC的周长为12cm
∴△A′B′C′的周长为12÷=16cm.
17.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
当∠D=∠B或∠E=∠C或时,△ADE∽△ACB.
故答案为:∠D=∠B或∠E=∠C或
18.解:设A、B两地的实际距离为x厘米,
根据题意得,
解得x=150000,
150000cm=1.5km.
故答案为1.5.
19.解:如图所示:
∵AB=AC,AD=CD,△ABC∽△DAC,
∴AC2=BC?AD,
∵AC=,AD=,
∴CB=2,
∵△ABC∽△DAC,
∴∠ACB=∠CAD,
∴CB∥AD,
∵AB=AC,F为BC中点,
∴AF⊥CB,BF=CF=1,
∴∠AFC=90°,
∵CB∥AD,
∴∠FAE=∠AFC=90°,
∵AC=,
∴AF=,
∵AD=,E为AD中点,
∴AE=,
∴EF===.
故答案为:.
20.解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=DA=DB,
∴∠ACD=∠DCB=45°,∠DCG=135°,
∵∠EDF=∠EDM=45°,DG=DM,
∴∠ADC=∠MDG,
∴∠ADM=∠CDG,
∴△ADM≌△CDG(SAS),
∴∠DAM=∠DCG=135°,
∵∠CAB=45°,
∴∠CAM=90°,
∴MH=GH===5k,
∵∠GDH=∠GAD=45°,∠DGH=∠AGD,
∴△DGH∽△AGD,
∴=,
∴DG2=GH?GA=40k2,
∵AC=BC=6,∠ACB=90°,
∴AB=AC=12,
∴AD=CD=6,
∵DJ⊥AC,
∴AJ=JC=3,DJ=AJ=IC=3,
∴GJ=8K﹣3,
在Rt△DJG中,∵DG2=DJ2+GJ2,
∴40k2=(8k﹣3)2+(3)2,
解得k=或(舍弃),
∴AH=3k=.
②如图2中,当点H在线段AC上,点G在AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:40k2=(8k﹣3)2+(3)2,
解得k=(舍弃)或,
∴AH=3k=.
③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:10k2=(3﹣2k)2+(3)2,
解得k=或﹣3(舍弃),
∴AH=3k=3,
综上所述,满足条件的AH的值为或或3.
故答案为或或3.
三.解答题
21.解:(1)设AP=2x,则PB=2x,AB=5x,
所以==;
(2)当AB=100时,=,
所以PB=60(cm).
22.解:(1)①∵内角为80°,
∴与它相邻内角的度数为100°.
∴菱形的“接近度”=|m﹣n|=|100﹣80|=20.
②当菱形的“接近度”等于0时,菱形是正方形.
故答案为:20;0;
(2)设矩形的长和宽分别为m,n(m≤n),如矩形的“接近度”的定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当=1时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
23.解:(1)∵AD是△ABC的中线,=,
∴=,
∵=,
∴=+,
∵G是重心,
∴=×(+)═+;
(2)延长BG交AC于H,
∵∠GAC=∠GCA,
∴GA=GC,
∵G是重心,AC=2,
∴AH=AC=1,
∴BH⊥AC,
在Rt△ABH中,∠AHB=90°,AB=3,
∴BH==2,
∴BG=BH=.
24.解:设===k,
则a=3k﹣2,b=4k,c=6k﹣5,
所以,2(3k﹣2)﹣4k+3(6k﹣5)=21,
解得k=2,
所以a=6﹣2=4,b=8,c=7,
所以a:b:c=4:8:7.
25.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
26.解:(1)∵DE∥BC,AD=2BD,
∴,
∴,(2分)
∵与方向相同,
∴,(2分)
∵=,
∴.(2分)
∵,
∴.(2分)
(2)作出的图形中,在方向上的分向量,
=+﹣=﹣+﹣(﹣+)=﹣+,
方向上的分向量==(+)=+.
27.(1)证明:∵AB=AC,∠A=36°,
∴∠ACB=(180°﹣36°)=72°,
∵CE平分∠ACB,
∴∠BCE=∠ACB=×72°=36°,
∴∠BCE=∠A=36°,
∴AE=BC,
又∵∠B=∠B,
∴△ABC∽△CBE,
∴=,
∴BC2=AB?BE,
即AE2=AB?BE,
∴E为线段AB的黄金分割点;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=180°﹣72°﹣36°=72°,
∴BC=CE,
由(1)已证AE=CE,
∴AE=CE=BC,
∴BC=?AB=×4=2﹣2.
相似三角形》单元测试卷
一.选择题
1.如果是非零向量,那么下列等式正确的是( )
A.=
B.=
C.
+=0
D.
+=0
2.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长为( )
A.3cm
B.4
cm
C.5cm
D.6
cm
3.已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为( )
A.
B.
C.
D.
4.下列图形中,一定相似的是( )
A.两个矩形
B.有一组角相等的两个等腰三角形
C.有一组对应角相等的两个菱形
D.两边对应成比例且有一组角相等的三角形
5.已知3a=2b(a≠0,b≠0),下列变形错误的是( )
A.
B.
C.
D.
6.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①;②;③;④,其中正确的结论是有( )个.
A.1
B.2
C.3
D.4
7.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A.
B.
C.
D.
8.如图,在矩形ABCD中,AB=2BC,E为CD上一点,且AE=AB,M为AE的中点.下列结论:
①DM=DA;②EB平分∠AEC;③S△ABE=S△ADE;④BE2=2AE?EC.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
9.若△ABC∽△DEF,它们的相似比为4:1,则△ABC与△DEF的周长比为( )
A.2:1
B.4:1
C.8:1
D.16:1
10.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为( )
A.10
B.
C.12
D.14
二.填空题
11.如图,在△ABC中,AB=AC=5,BC=8,中线AD、CE相交于点F,则AF的长为
.
12.如果2x=5y(y≠0),那么=
.
13.已知:在平行四边形ABCD中,设=,=,那么=
(用向量、的式子表示).
14.已知点P是线段AB的黄金分割点,AP>PB.若AB=2,则AP=
.
15.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=
.
16.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为
cm.
17.如图,∠1=∠2,添加一个条件使得△ADE∽△ACB,可添加的条件是
.
18.在比例尺为1:30000的地图上,量得A、B两地的图上距离AB=5cm,则A、B两地的实际距离为
km.
19.如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC=,AD=CD=,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于
.
20.如图,在等腰Rt△ABC中,AC=BC=6,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若=,则AH的长为
.
三.解答题
21.已知P为线段AB上一点,且AB被点P分为AP:PB=2:3.
(1)求AB:BP;
(2)如果AB=100cm,试求PB的长.
22.如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α﹣β|,于是|α﹣β|越小,菱形越接近正方形.
①若菱形的一个内角为80°,则该菱形的“接近度”为
;
②当菱形的“接近度”等于
时,菱形是正方形;
(2)设矩形的长和宽分别为m,n(m≤n),试写出矩形的“接近度”的合理定义.
23.如图,已知AD是△ABC的中线,G是重心.
(1)设=,=,用向量、表示;
(2)如果AB=3,AC=2,∠GAC=∠GCA,求BG的长.
24.若,且2a﹣b+3c=21.试求a:b:c.
25.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
26.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD=2BD,已知,.
(1)用向量、分别表示向量、;
(2)作出向量分别在、方向上的分向量(写出结论,不要求写作法).
27.如图,△ABC中,AB=AC,∠A=36°,CE平分∠ACB交AB于点E,
(1)试说明点E为线段AB的黄金分割点;
(2)若AB=4,求BC的长.
参考答案与试题解析
一.选择题
1.解:∵是非零向量,
∴||=||.
故选:A.
2.解:已知a,b,c,d是成比例线段,
根据比例线段的定义得:ad=cb,
代入a=3cm,b=2cm,c=6cm,
解得:d=4,
则d=4cm.
故选:B.
3.解:根据题意得AP=AB,
所以PB=AB﹣AP=AB,
所以PB:AB=.
故选:B.
4.解:A、两个矩形对应边的比值不一定相等,故此选项错误;
B、有一组角相等的两个等腰三角形,有可能是两三角形的底角与顶角对应相等,故此选项错误;
C、有一组对应角相等的两个菱形,相似,故此选项正确;
D、两边对应成比例且两边的夹角相等的三角形相似,故此选项错误.
故选:C.
5.解:A、∵3a=2b,
∴两边都除以3b得:=,故本选项不符合题意;
B、∵3a=2b,
∴两边都除以2a得:=,故本选项符合题意;
C、3a=2b,
∴两边都除以2a得:=,故本选项不符合题意;
D、∵3a=2b,
∴两边都除以6得:=,故本选项不符合题意;
故选:B.
6.解:∵AD=DB,AE=EC,
∴DE∥BC,DE:BC=1:2,
∴==,故①③正确,
设S△DOE=S,则S△EOC=2S,S△BOC=4s,
∴=,故②错误,
∵DE∥BC,
∴=1,故④错误,
故选:B.
7.解:根据题意得:AB==,AC=2,BC==,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
8.解:①∵在直角△ADE中,∠ADE=90°,M为AE的中点,∴DM=AE,∵AE=AB,AB=2BC=2DA,∴DM=DA,正确;
②在直角△ADE中,∠ADE=90°,AD=AE,∴∠DEA=30°.∵CD∥AB,∴∠EAB=∠DEA=30°,∠CEB=∠ABE.在△EAB中,∠EAB=30°,AE=AB,∴∠AEB=∠ABE=75°,∴∠CEB=75°,∴EB平分∠AEC,正确;
③∵S△ABE=S矩形ABCD,S△ADE<S△ADC=S矩形ABCD,∴S△ABE>S△ADE,错误;
④在矩形ABCD中,设BC=DA=a,则AE=AB=DC=2BC=2a,DE=AD=a,∴EC=(2﹣)a.在直角△BCE中,BE2=BC2+CE2=a2+[(2﹣)a]2=(8﹣4)a2,2AE?EC=2×2a×(2﹣)a=(8﹣4)a2,正确.
故选:C.
9.解:∵△ABC∽△DEF,它们的相似比为4:1,
∴△ABC与△DEF的周长的比为:4:1.
故选:B.
10.解:∵l1∥l2∥l3,
∴==,
∵DE=4,
∴EF=10,
∴DF=DE+EF=4+10=14,
故选:D.
二.填空题
11.解:∵AB=AC,AD为中线,
∴AD⊥BC,BD=CD=BC=4,
在Rt△ABD中,AD==3,
∵点F为中线AD、CE的交点,
∴F点为△ABC的重心,
∴AF=AD=×3=2.
故答案为2.
12.解:∵2x=5y(y≠0),
∴=.
故答案为:.
13.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴==,
∵=,
∴=﹣,=﹣,
∴=+=﹣﹣.
故答案为:﹣﹣.
14.解:由于P为线段AB=2的黄金分割点,
且AP是较长线段;
则AP=2×=﹣1.
15.解:∵线段AD、BE是△ABC的中线,
∴=,=,
∵EF∥BC,=,
∴=.
故答案为:.
16.解:∵△ABC∽△A′B′C′,且,即相似三角形的相似比是
∵△ABC的周长为12cm
∴△A′B′C′的周长为12÷=16cm.
17.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
当∠D=∠B或∠E=∠C或时,△ADE∽△ACB.
故答案为:∠D=∠B或∠E=∠C或
18.解:设A、B两地的实际距离为x厘米,
根据题意得,
解得x=150000,
150000cm=1.5km.
故答案为1.5.
19.解:如图所示:
∵AB=AC,AD=CD,△ABC∽△DAC,
∴AC2=BC?AD,
∵AC=,AD=,
∴CB=2,
∵△ABC∽△DAC,
∴∠ACB=∠CAD,
∴CB∥AD,
∵AB=AC,F为BC中点,
∴AF⊥CB,BF=CF=1,
∴∠AFC=90°,
∵CB∥AD,
∴∠FAE=∠AFC=90°,
∵AC=,
∴AF=,
∵AD=,E为AD中点,
∴AE=,
∴EF===.
故答案为:.
20.解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=DA=DB,
∴∠ACD=∠DCB=45°,∠DCG=135°,
∵∠EDF=∠EDM=45°,DG=DM,
∴∠ADC=∠MDG,
∴∠ADM=∠CDG,
∴△ADM≌△CDG(SAS),
∴∠DAM=∠DCG=135°,
∵∠CAB=45°,
∴∠CAM=90°,
∴MH=GH===5k,
∵∠GDH=∠GAD=45°,∠DGH=∠AGD,
∴△DGH∽△AGD,
∴=,
∴DG2=GH?GA=40k2,
∵AC=BC=6,∠ACB=90°,
∴AB=AC=12,
∴AD=CD=6,
∵DJ⊥AC,
∴AJ=JC=3,DJ=AJ=IC=3,
∴GJ=8K﹣3,
在Rt△DJG中,∵DG2=DJ2+GJ2,
∴40k2=(8k﹣3)2+(3)2,
解得k=或(舍弃),
∴AH=3k=.
②如图2中,当点H在线段AC上,点G在AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:40k2=(8k﹣3)2+(3)2,
解得k=(舍弃)或,
∴AH=3k=.
③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:10k2=(3﹣2k)2+(3)2,
解得k=或﹣3(舍弃),
∴AH=3k=3,
综上所述,满足条件的AH的值为或或3.
故答案为或或3.
三.解答题
21.解:(1)设AP=2x,则PB=2x,AB=5x,
所以==;
(2)当AB=100时,=,
所以PB=60(cm).
22.解:(1)①∵内角为80°,
∴与它相邻内角的度数为100°.
∴菱形的“接近度”=|m﹣n|=|100﹣80|=20.
②当菱形的“接近度”等于0时,菱形是正方形.
故答案为:20;0;
(2)设矩形的长和宽分别为m,n(m≤n),如矩形的“接近度”的定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当=1时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
23.解:(1)∵AD是△ABC的中线,=,
∴=,
∵=,
∴=+,
∵G是重心,
∴=×(+)═+;
(2)延长BG交AC于H,
∵∠GAC=∠GCA,
∴GA=GC,
∵G是重心,AC=2,
∴AH=AC=1,
∴BH⊥AC,
在Rt△ABH中,∠AHB=90°,AB=3,
∴BH==2,
∴BG=BH=.
24.解:设===k,
则a=3k﹣2,b=4k,c=6k﹣5,
所以,2(3k﹣2)﹣4k+3(6k﹣5)=21,
解得k=2,
所以a=6﹣2=4,b=8,c=7,
所以a:b:c=4:8:7.
25.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
26.解:(1)∵DE∥BC,AD=2BD,
∴,
∴,(2分)
∵与方向相同,
∴,(2分)
∵=,
∴.(2分)
∵,
∴.(2分)
(2)作出的图形中,在方向上的分向量,
=+﹣=﹣+﹣(﹣+)=﹣+,
方向上的分向量==(+)=+.
27.(1)证明:∵AB=AC,∠A=36°,
∴∠ACB=(180°﹣36°)=72°,
∵CE平分∠ACB,
∴∠BCE=∠ACB=×72°=36°,
∴∠BCE=∠A=36°,
∴AE=BC,
又∵∠B=∠B,
∴△ABC∽△CBE,
∴=,
∴BC2=AB?BE,
即AE2=AB?BE,
∴E为线段AB的黄金分割点;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=180°﹣72°﹣36°=72°,
∴BC=CE,
由(1)已证AE=CE,
∴AE=CE=BC,
∴BC=?AB=×4=2﹣2.
