曹冬冬 矩形PPT
图片预览



文档简介
(共22张PPT)
19.2 特殊的平行四边形
19.2.1 矩形
自学思考:
阅读课本P94——P95内容,并思考:
①什么叫矩形?它是平行四边形吗?它有哪些不同于平行四边形的特殊性质?
②直角三角形斜边上中线有什么性质?与此相类似的性质还有什么?
③如何证明矩形的性质和直角三角形斜边上中线的性质?
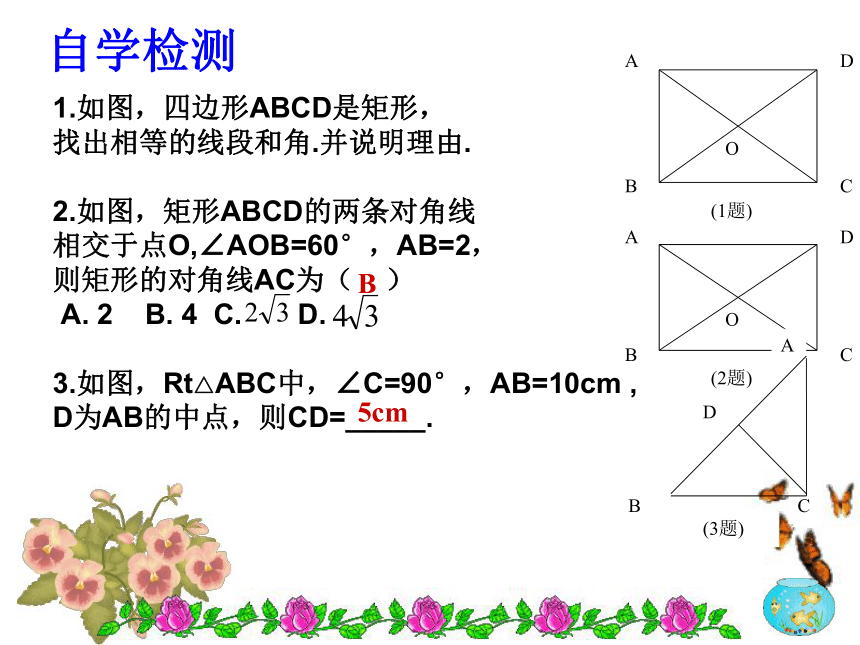
1.如图,四边形ABCD是矩形,
找出相等的线段和角.并说明理由.
2.如图,矩形ABCD的两条对角线
相交于点O,∠AOB=60°,AB=2,
则矩形的对角线AC为( )
A. 2 B. 4 C. D.
3.如图,Rt△ABC中,∠C=90°,AB=10cm ,
D为AB的中点,则CD=_____.
O
A
C
B
D
(1题)
O
A
C
B
D
(2题)
A
C
D
B
(3题)
自学检测
5cm
B
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
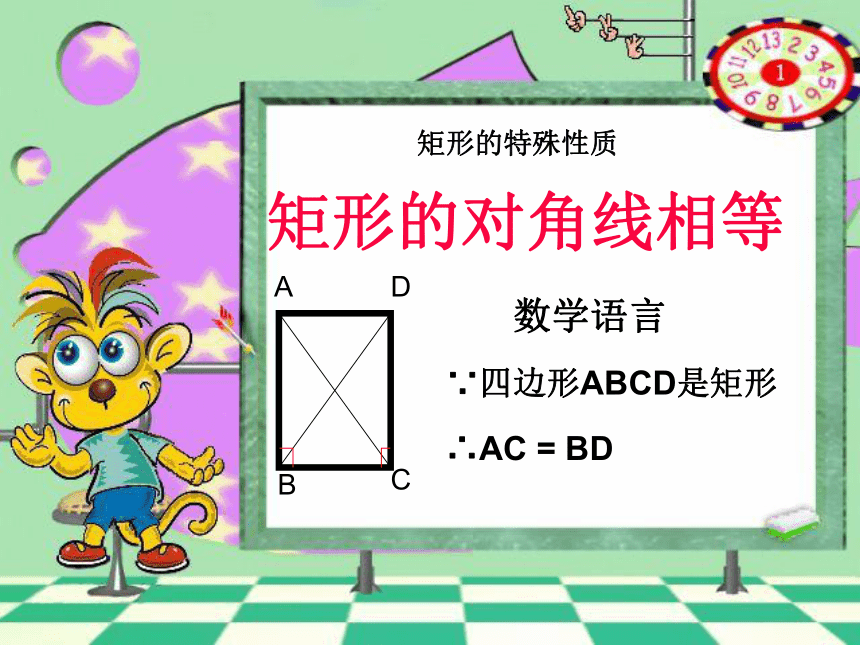
矩形的特殊性质
矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
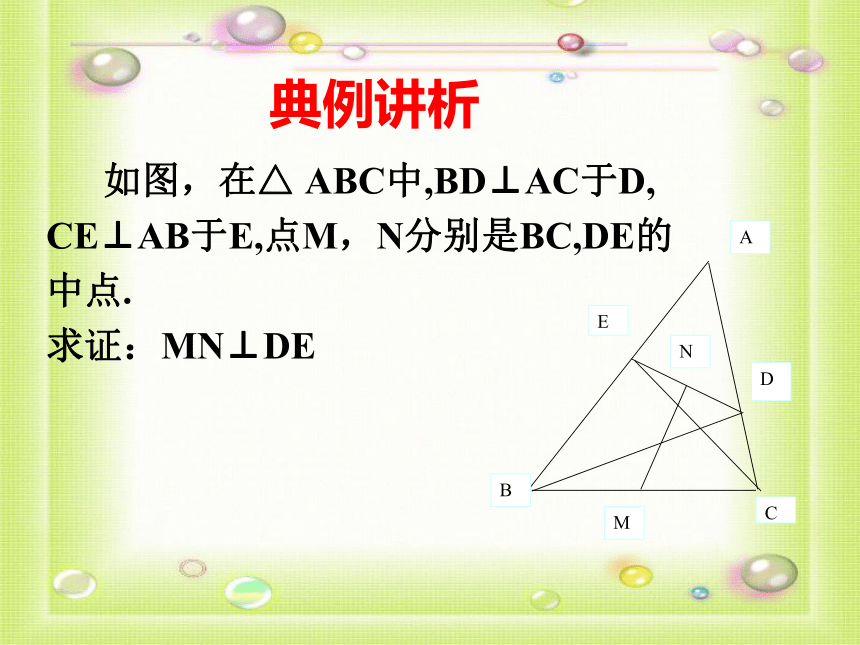
如图,在△ ABC中,BD⊥AC于D,
CE⊥AB于E,点M,N分别是BC,DE的
中点.
求证:MN⊥DE
典例讲析
A
C
B
M
D
E
N
有一株牵牛花沿一根直径为4cm的竹竿向上攀援生长,若牵牛花每缠绕竹竿一圈,它的茎就会爬升5cm。请问像这样缠绕两圈,牵牛花的茎能生长多长?
A
C
B
M
D
E
N
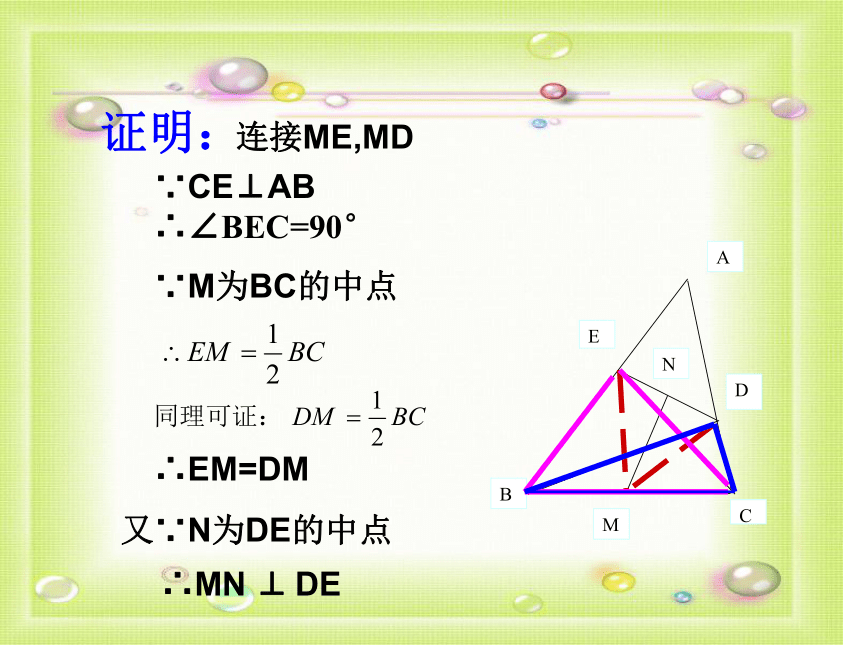
连接ME,MD
证明:
∵CE⊥AB
∴∠BEC=90°
∵M为BC的中点
∴EM=DM
又∵N为DE的中点
∴MN ⊥ DE
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
1.(2010福建龙岩)如图(1),在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AC=8,则EF=_____.
2. 如图(2),在Rt △ ABC中,∠ACB=90°,AC=4,BC=3,点D是AB的中点,CD的长为_____.
营中热身
A
C
O
D
B
E
F
(1)
A
C
D
B
(2)
2
2.5
3.如图(3),在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.
求证:BE=CF.
营中寻宝
O
B
A
E
F
C
D
(3)
矩形的四个角都是直角.
※ 矩形的性质:
矩形的对角线相等.
矩形具有平行四边形的所有性质.
※ 直角三角形的一个性质 :
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
矩形是轴对称图形.
必做题:P 102 4. P103 9.
选做题:如图,在矩形ABCD中,AE⊥BD于E,对角线AC,BD相交于点O,且BE:ED=1:3,
AD=6cm,求AE的长。
O
A
C
B
D
E
课外作业
课后思考
(2010浙江舟山)如图(4),在△ ABC中,D是
BC边上的一点,E是AD的中点,过A点作BC的
平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点。
(2)如果AB=AC,试判断四边形AFBD的形状,并说
明你的结论。
B
F
D
C
A
E
(4)
课后预习
预习内容: 课本P95----P96.
学习目标:
①理解并掌握矩形的判定条件,会判断一个四边形是矩形。
②综合运用矩形的性质和判定方法进行计算和证明。
19.2 特殊的平行四边形
19.2.1 矩形
自学思考:
阅读课本P94——P95内容,并思考:
①什么叫矩形?它是平行四边形吗?它有哪些不同于平行四边形的特殊性质?
②直角三角形斜边上中线有什么性质?与此相类似的性质还有什么?
③如何证明矩形的性质和直角三角形斜边上中线的性质?
1.如图,四边形ABCD是矩形,
找出相等的线段和角.并说明理由.
2.如图,矩形ABCD的两条对角线
相交于点O,∠AOB=60°,AB=2,
则矩形的对角线AC为( )
A. 2 B. 4 C. D.
3.如图,Rt△ABC中,∠C=90°,AB=10cm ,
D为AB的中点,则CD=_____.
O
A
C
B
D
(1题)
O
A
C
B
D
(2题)
A
C
D
B
(3题)
自学检测
5cm
B
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
矩形的特殊性质
矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
如图,在△ ABC中,BD⊥AC于D,
CE⊥AB于E,点M,N分别是BC,DE的
中点.
求证:MN⊥DE
典例讲析
A
C
B
M
D
E
N
有一株牵牛花沿一根直径为4cm的竹竿向上攀援生长,若牵牛花每缠绕竹竿一圈,它的茎就会爬升5cm。请问像这样缠绕两圈,牵牛花的茎能生长多长?
A
C
B
M
D
E
N
连接ME,MD
证明:
∵CE⊥AB
∴∠BEC=90°
∵M为BC的中点
∴EM=DM
又∵N为DE的中点
∴MN ⊥ DE
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
1.(2010福建龙岩)如图(1),在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AC=8,则EF=_____.
2. 如图(2),在Rt △ ABC中,∠ACB=90°,AC=4,BC=3,点D是AB的中点,CD的长为_____.
营中热身
A
C
O
D
B
E
F
(1)
A
C
D
B
(2)
2
2.5
3.如图(3),在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.
求证:BE=CF.
营中寻宝
O
B
A
E
F
C
D
(3)
矩形的四个角都是直角.
※ 矩形的性质:
矩形的对角线相等.
矩形具有平行四边形的所有性质.
※ 直角三角形的一个性质 :
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
矩形是轴对称图形.
必做题:P 102 4. P103 9.
选做题:如图,在矩形ABCD中,AE⊥BD于E,对角线AC,BD相交于点O,且BE:ED=1:3,
AD=6cm,求AE的长。
O
A
C
B
D
E
课外作业
课后思考
(2010浙江舟山)如图(4),在△ ABC中,D是
BC边上的一点,E是AD的中点,过A点作BC的
平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点。
(2)如果AB=AC,试判断四边形AFBD的形状,并说
明你的结论。
B
F
D
C
A
E
(4)
课后预习
预习内容: 课本P95----P96.
学习目标:
①理解并掌握矩形的判定条件,会判断一个四边形是矩形。
②综合运用矩形的性质和判定方法进行计算和证明。
