等腰三角形性质讲学稿(无答案)
文档属性
| 名称 | 等腰三角形性质讲学稿(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 29.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-07 00:00:00 | ||
图片预览

文档简介
课题 等腰三角形性质
课型 新授 主备教师 方翔芝 班别 姓名
学习目标:1、理解等腰三角形是轴对称图形;
2、掌握等边对等角的性质;
3、掌握“三线合一”的性质;
重点难点:等边对等角,“三线合一”性质的应用。
学习过程:
一、课前准备:
1、如果一个图形沿 折叠,直线两旁的部分能够互相 ,这个图形叫做轴对称图形,这条直线就是它的 。 轴对称图形的对称轴是任何一对 所连线段的 。
有 边相等的三角形叫等腰三角形。
观察图中的等腰△ABC和等腰△DEF。请学生在图上分别标出它们的腰、底边、顶角、底角并写出下面公式:
等腰三角形周长=底边+ 底角
(2)等腰三角形的内角和:顶角+ 底角=180。
推出:顶角= 底角=
4、(1)等腰三角形的周长是10,腰长是4,则底边为______
(2)等腰三角形的周长是20cm,一边长是8cm,则其它两边长为____
(3)已知等腰三角形的腰长比底边多2cm,并且它的周长为16cm.求这个等腰三角形的边长.
5、证明两个三角形全等的方法有 。
6、预习时还有哪些疑难问题?
二、探索新知:(合作、讨论、交流)
1、操作、实践:
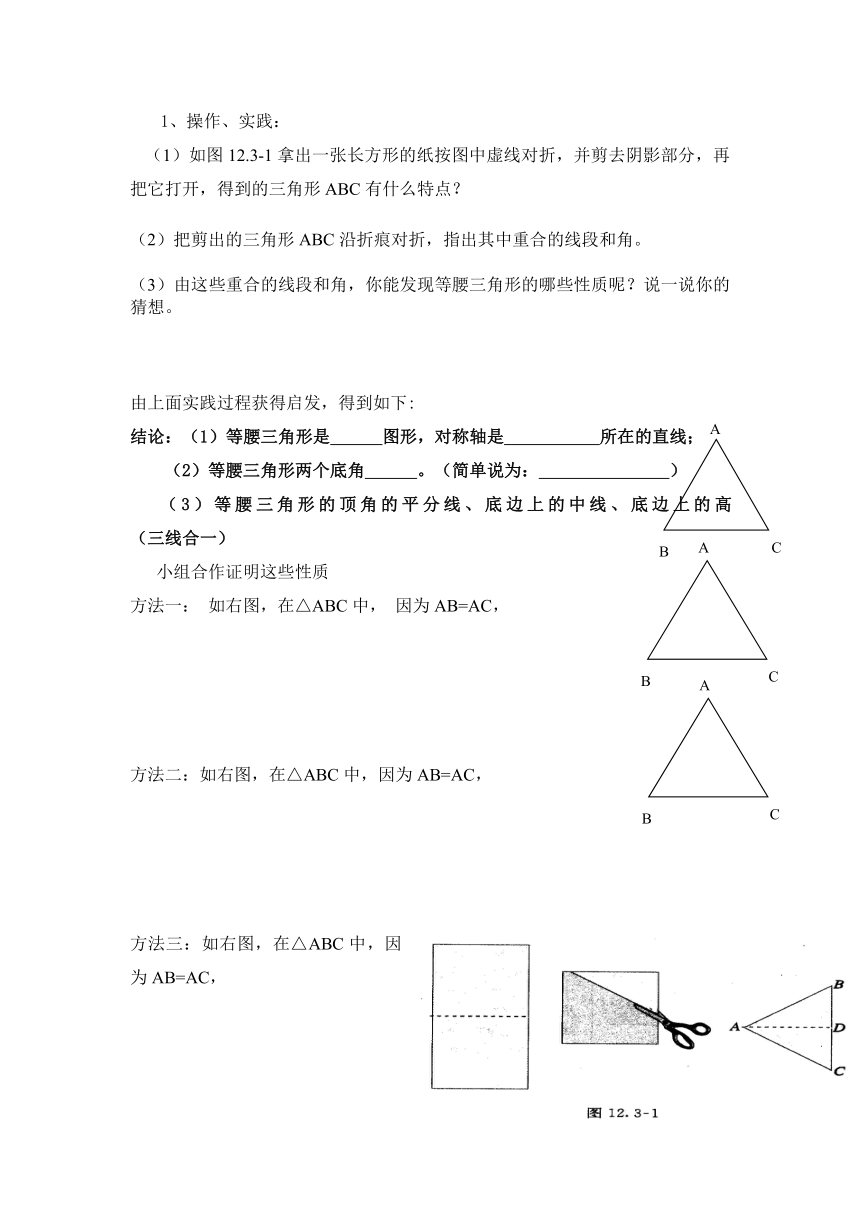
(1)如图12.3-1拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的三角形ABC有什么特点?
(2)把剪出的三角形ABC沿折痕对折,指出其中重合的线段和角。
(3)由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。
由上面实践过程获得启发,得到如下:
结论:(1)等腰三角形是 图形,对称轴是 所在的直线;
(2)等腰三角形两个底角 。(简单说为: )
(3)等腰三角形的顶角的平分线、底边上的中线、底边上的高 (三线合一)
小组合作证明这些性质
方法一: 如右图,在△ABC中, 因为AB=AC,
方法二:如右图,在△ABC中,因为AB=AC,
方法三:如右图,在△ABC中,因为AB=AC,
三、应用举例
例1 (1)等腰三角形的一个底角是70度,则它的顶角是______
(2)等腰三角形的一个角是30度,则它的顶角是______
例2.在△ABC中,AB=AC,点D在BC上,且CD=BD,找出图中相等的角并说明理由。
解:
例3. 在△ABC中,AB=AC,AD⊥BC垂足为点D,DE⊥AB于点E,DF⊥AC于F,那么DE与DF相等吗 为什么
小结:
学习体会
本节课你有哪些收获?
预习时的疑难解决了吗?你还有哪些疑惑?
你认为这节课还有那些需要注意或需要改正的地方?
五、自我测试
1、在△ABC中,AB=AC,
(1)如果∠A=70°,则∠C=_________,∠B=___________
(2)如果∠A=90°,则∠B=_________,∠C=___________
(3)如果有一个角等于120°,则其余两个角分别是多少度?
(4)如果有一个角等于55°,则其余两个角分别是多少度?
2、如果△ABC是轴对称图形,则它的对称轴一定是( )
A.某一条边上的高; B.某一条边上的中线
C.平分一角和这个角对边的直线; D.某一个角的平分线
3.如图,房屋的屋顶∠BAC=110°,过屋顶A的立柱AD⊥BC,屋檐AB=AC,试计算∠B、∠C、∠BAD、∠CAD的度数,说明理由。
4、△ABC中,AB=AC点D在AC上,BD=BC=AD,求△ABC各角的度数.
5、已知ABC中,AB=AC,BD=CD,AD的延长线交BC于点E。求证:AE⊥BC
六、拓展延伸
1、如图,已知:在△ABC中,∠BAC=90°,BD平分∠ABC,DE⊥BC于E。
试说明BD垂直平分AE
2、已知点A和点B,以A点和B点为其中的两个顶点作位置不同的等腰直角三角形,可以作( )
A 2个 B 4个 C 6个 D 3个
F
A
B
C
E
D
A
B
C
A
B
C
A
B
C
1
2
3
A
B
C
D
A
B
C
D
_
A
_
D
_
B
_
C
A
B
D
E
C
课型 新授 主备教师 方翔芝 班别 姓名
学习目标:1、理解等腰三角形是轴对称图形;
2、掌握等边对等角的性质;
3、掌握“三线合一”的性质;
重点难点:等边对等角,“三线合一”性质的应用。
学习过程:
一、课前准备:
1、如果一个图形沿 折叠,直线两旁的部分能够互相 ,这个图形叫做轴对称图形,这条直线就是它的 。 轴对称图形的对称轴是任何一对 所连线段的 。
有 边相等的三角形叫等腰三角形。
观察图中的等腰△ABC和等腰△DEF。请学生在图上分别标出它们的腰、底边、顶角、底角并写出下面公式:
等腰三角形周长=底边+ 底角
(2)等腰三角形的内角和:顶角+ 底角=180。
推出:顶角= 底角=
4、(1)等腰三角形的周长是10,腰长是4,则底边为______
(2)等腰三角形的周长是20cm,一边长是8cm,则其它两边长为____
(3)已知等腰三角形的腰长比底边多2cm,并且它的周长为16cm.求这个等腰三角形的边长.
5、证明两个三角形全等的方法有 。
6、预习时还有哪些疑难问题?
二、探索新知:(合作、讨论、交流)
1、操作、实践:
(1)如图12.3-1拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的三角形ABC有什么特点?
(2)把剪出的三角形ABC沿折痕对折,指出其中重合的线段和角。
(3)由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。
由上面实践过程获得启发,得到如下:
结论:(1)等腰三角形是 图形,对称轴是 所在的直线;
(2)等腰三角形两个底角 。(简单说为: )
(3)等腰三角形的顶角的平分线、底边上的中线、底边上的高 (三线合一)
小组合作证明这些性质
方法一: 如右图,在△ABC中, 因为AB=AC,
方法二:如右图,在△ABC中,因为AB=AC,
方法三:如右图,在△ABC中,因为AB=AC,
三、应用举例
例1 (1)等腰三角形的一个底角是70度,则它的顶角是______
(2)等腰三角形的一个角是30度,则它的顶角是______
例2.在△ABC中,AB=AC,点D在BC上,且CD=BD,找出图中相等的角并说明理由。
解:
例3. 在△ABC中,AB=AC,AD⊥BC垂足为点D,DE⊥AB于点E,DF⊥AC于F,那么DE与DF相等吗 为什么
小结:
学习体会
本节课你有哪些收获?
预习时的疑难解决了吗?你还有哪些疑惑?
你认为这节课还有那些需要注意或需要改正的地方?
五、自我测试
1、在△ABC中,AB=AC,
(1)如果∠A=70°,则∠C=_________,∠B=___________
(2)如果∠A=90°,则∠B=_________,∠C=___________
(3)如果有一个角等于120°,则其余两个角分别是多少度?
(4)如果有一个角等于55°,则其余两个角分别是多少度?
2、如果△ABC是轴对称图形,则它的对称轴一定是( )
A.某一条边上的高; B.某一条边上的中线
C.平分一角和这个角对边的直线; D.某一个角的平分线
3.如图,房屋的屋顶∠BAC=110°,过屋顶A的立柱AD⊥BC,屋檐AB=AC,试计算∠B、∠C、∠BAD、∠CAD的度数,说明理由。
4、△ABC中,AB=AC点D在AC上,BD=BC=AD,求△ABC各角的度数.
5、已知ABC中,AB=AC,BD=CD,AD的延长线交BC于点E。求证:AE⊥BC
六、拓展延伸
1、如图,已知:在△ABC中,∠BAC=90°,BD平分∠ABC,DE⊥BC于E。
试说明BD垂直平分AE
2、已知点A和点B,以A点和B点为其中的两个顶点作位置不同的等腰直角三角形,可以作( )
A 2个 B 4个 C 6个 D 3个
F
A
B
C
E
D
A
B
C
A
B
C
A
B
C
1
2
3
A
B
C
D
A
B
C
D
_
A
_
D
_
B
_
C
A
B
D
E
C
