算术平方根
图片预览





文档简介
(共22张PPT)
希伯索斯
无理数
有理数
第十三章 实 数
研究从这里开始
4
如图:有一张正方形纸片,它的边长是2.
(1)它的面积是多少?
研究从这里开始
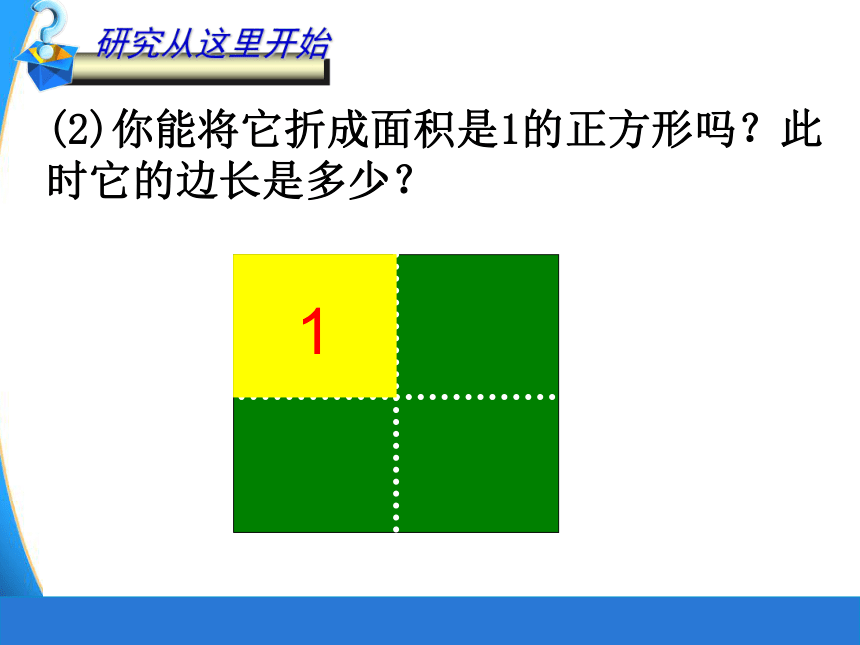
(2)你能将它折成面积是1的正方形吗?此时它的边长是多少?
1
研究从这里开始
(3)你能将它折成面积是2的正方形吗?此时它的边长是多少?
1
2
----算术平方根
义务教育课程标准试验教科书八年级上册《数学》
(1) 理解算术平方根的概念,会用根号表示一个
数的算术平方根.
(2) 了解求一个正数的算术平方根与平方运算的互
逆关系,会用平方运算求某些非负数的算术平
方根.
探 索 与 发 现
正方形的边长
(x) 正方形的
面积
(a)
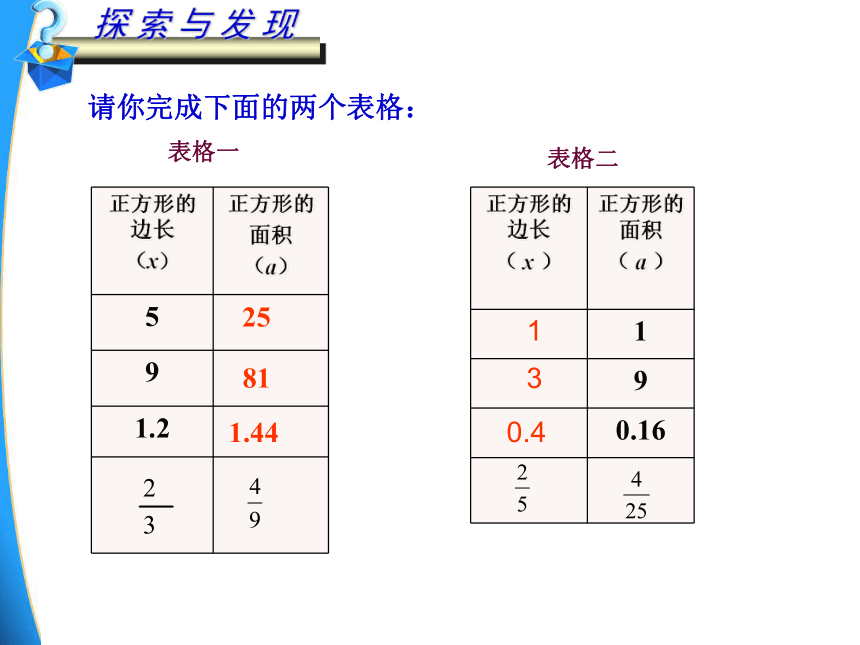
5
9
1.2
25
81
1.44
表格一
请你完成下面的两个表格:
正方形的边长
( x ) 正方形的面积
( a )
1
9
0.16
1
3
0.4
表格二
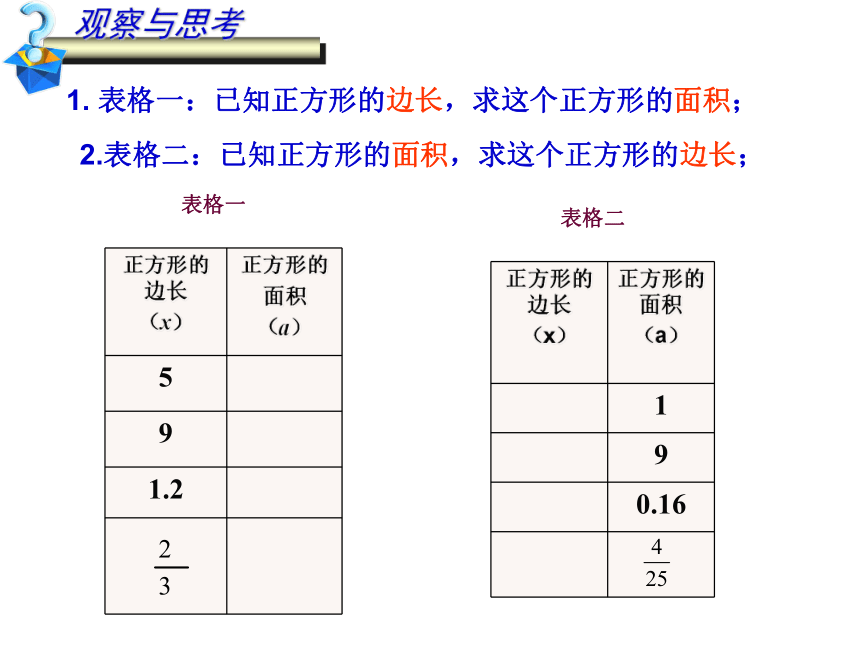
1. 表格一:已知正方形的边长,求这个正方形的面积;
观察与思考
正方形的边长
(x) 正方形的
面积
(a)
5
9
1.2
表格一
正方形的边长
(x) 正方形的面积
(a)
1
9
0.16
表格二
2.表格二:已知正方形的面积,求这个正方形的边长;
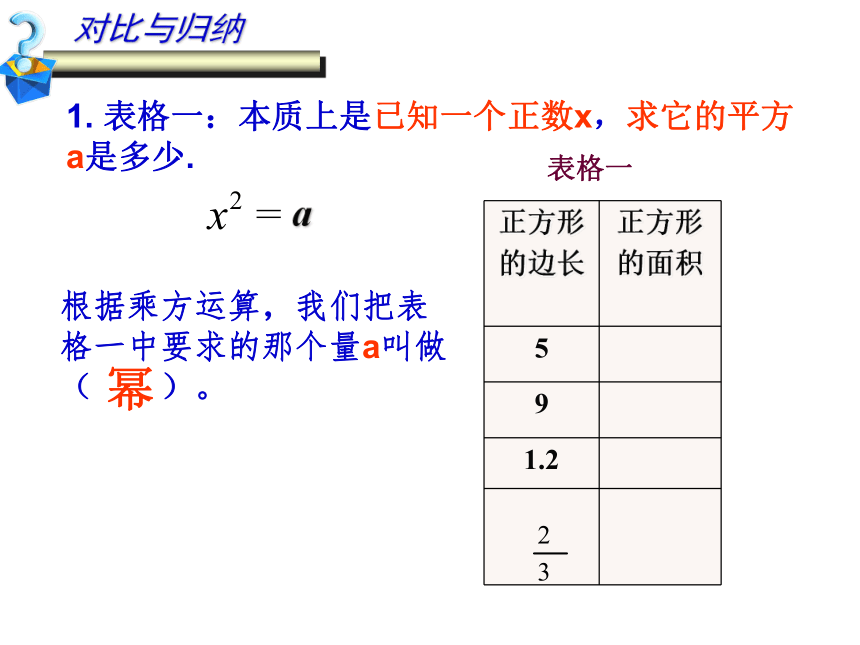
1. 表格一:本质上是已知一个正数x,求它的平方a是多少.
对比与归纳
正方形
的边长 正方形
的面积
5
9
1.2
表格一
根据乘方运算,我们把表格一中要求的那个量a叫做( )。
幂
= a
对比与归纳
2.表格二:本质上是已知 一个正数x 的平方是a ,求这个正数 x是多少.
= a
这里我们赋予要求的这个正数“x”一个新的意义-----把要求的正数x,叫做已知正数a的
正方形
的边长
(x) 正方形
的面积
(a)
1
9
0.16
表格二
算术平方根.
归纳与概括
∣揭示本质的属性
算术平方根的定义
一般地,如果一个正数x的平方等于a,
即 ,那么这个正数x叫做a的算
术平方根。
=a
规定:0的算术平方根是0.
正方形
的边长
正方形
的面积
1
1
3
9
感受概念
而正数1的平方等于1,所以1叫做1的算术平方根。
而正数3的平方等于9,所以3叫做9的算术平方根。
因为正数x的平方等于a,正数x叫a的算术平方根。
因为正数x的平方等于a,正数x叫a的算术平方根。
正方形的边长
正方形的面积
0.4
0.16
感受概念
因为正数x的平方等于a,正数x叫a的算术平方根。
而正数0.4的平方等于0.16,所以0.4叫做0.16的算术平方根。
而正数 的平方等于 ,所以
叫做 的算术平方根。
因为正数x的平方等于a,正数x叫a的算术平方根。
明辨是非
√
∣加深对概念的理解
请你判断下列说法是否正确,并说明理由:
(1) 3 是9 的算术平方根; ( )
(2) 9是3的算术平方根; ( )
(3)-1 是1的算术平方根;( )
(4)-100的算术平方根是10;( )
(5) 因为23 = 8, 所以 2 是 8 的算术平方根;( )
(6) 5是10的算术平方根. ( )
×
×
×
×
×
巩固与应用
明辨是非
∣加深对概念的理解
请你判断下列说法是否正确,并说明理由:
(1) 3 是9 的算术平方根; (√ )
(2) 9是3的算术平方根; ( × )
(3)-1 是1的算术平方根;( × )
(4)-100的算术平方根是10;(× )
(5) 因为23 = 8, 所以 2 是 8 的算术平方根;( × )
(6) 5是10的算术平方根. ( × )
巩固与应用
已知一个正数的平方,
求这个正数;
负数没有算术平方根;
算术平方根没有负数;
归纳与概括
∣揭示本质的属性
综合以上探究结果,我们可以得到:
非负数都有算术平方根,
算术平方根都是非负数 .
归纳与概括
∣揭示本质的属性
算术平方根用符号表示如下
如果 x2=a(x≥0),则x= .
a的算术平方根记作 ,读作“根号a”,
a叫做被开方数。
填空:
1.16的算术平方根用符号表示为
2.100的算术平方根用符号表示为
4. 符号 表示的意义为
5. 符号 表示的意义为
学以致用
6. 符号 表示的意义为
3.2的算术平方根用符号表示为
25的算术平方根
17的算术平方根
的算术平方根
∣加深对概念的理解
巩固与应用
(1)求下列各数的算术平方根.
① 144 ②
③ 32
(2)求下列各式的值.
① ② ③
=0.3
=
=2
计算:
解:因为 =144,
所以 =12.
解:因为 = ,
所以 =3.
解:因为 = ,
所以 = .
回 顾 与 反 思
——让我们的认识升华
这节课我们学习了什么数学概念?
我们获得这个概念,经历了怎样的过程?
通过这个过程,你有什么感受和体会?
根据你对算术平方根的理解,
现在你能解释 的意义吗?
2
本节作业
课本p69练习题第1,2题
必做题:
试探究非负数a与a的算术平方根的大小关系.
选做题:
希伯索斯
无理数
有理数
第十三章 实 数
研究从这里开始
4
如图:有一张正方形纸片,它的边长是2.
(1)它的面积是多少?
研究从这里开始
(2)你能将它折成面积是1的正方形吗?此时它的边长是多少?
1
研究从这里开始
(3)你能将它折成面积是2的正方形吗?此时它的边长是多少?
1
2
----算术平方根
义务教育课程标准试验教科书八年级上册《数学》
(1) 理解算术平方根的概念,会用根号表示一个
数的算术平方根.
(2) 了解求一个正数的算术平方根与平方运算的互
逆关系,会用平方运算求某些非负数的算术平
方根.
探 索 与 发 现
正方形的边长
(x) 正方形的
面积
(a)
5
9
1.2
25
81
1.44
表格一
请你完成下面的两个表格:
正方形的边长
( x ) 正方形的面积
( a )
1
9
0.16
1
3
0.4
表格二
1. 表格一:已知正方形的边长,求这个正方形的面积;
观察与思考
正方形的边长
(x) 正方形的
面积
(a)
5
9
1.2
表格一
正方形的边长
(x) 正方形的面积
(a)
1
9
0.16
表格二
2.表格二:已知正方形的面积,求这个正方形的边长;
1. 表格一:本质上是已知一个正数x,求它的平方a是多少.
对比与归纳
正方形
的边长 正方形
的面积
5
9
1.2
表格一
根据乘方运算,我们把表格一中要求的那个量a叫做( )。
幂
= a
对比与归纳
2.表格二:本质上是已知 一个正数x 的平方是a ,求这个正数 x是多少.
= a
这里我们赋予要求的这个正数“x”一个新的意义-----把要求的正数x,叫做已知正数a的
正方形
的边长
(x) 正方形
的面积
(a)
1
9
0.16
表格二
算术平方根.
归纳与概括
∣揭示本质的属性
算术平方根的定义
一般地,如果一个正数x的平方等于a,
即 ,那么这个正数x叫做a的算
术平方根。
=a
规定:0的算术平方根是0.
正方形
的边长
正方形
的面积
1
1
3
9
感受概念
而正数1的平方等于1,所以1叫做1的算术平方根。
而正数3的平方等于9,所以3叫做9的算术平方根。
因为正数x的平方等于a,正数x叫a的算术平方根。
因为正数x的平方等于a,正数x叫a的算术平方根。
正方形的边长
正方形的面积
0.4
0.16
感受概念
因为正数x的平方等于a,正数x叫a的算术平方根。
而正数0.4的平方等于0.16,所以0.4叫做0.16的算术平方根。
而正数 的平方等于 ,所以
叫做 的算术平方根。
因为正数x的平方等于a,正数x叫a的算术平方根。
明辨是非
√
∣加深对概念的理解
请你判断下列说法是否正确,并说明理由:
(1) 3 是9 的算术平方根; ( )
(2) 9是3的算术平方根; ( )
(3)-1 是1的算术平方根;( )
(4)-100的算术平方根是10;( )
(5) 因为23 = 8, 所以 2 是 8 的算术平方根;( )
(6) 5是10的算术平方根. ( )
×
×
×
×
×
巩固与应用
明辨是非
∣加深对概念的理解
请你判断下列说法是否正确,并说明理由:
(1) 3 是9 的算术平方根; (√ )
(2) 9是3的算术平方根; ( × )
(3)-1 是1的算术平方根;( × )
(4)-100的算术平方根是10;(× )
(5) 因为23 = 8, 所以 2 是 8 的算术平方根;( × )
(6) 5是10的算术平方根. ( × )
巩固与应用
已知一个正数的平方,
求这个正数;
负数没有算术平方根;
算术平方根没有负数;
归纳与概括
∣揭示本质的属性
综合以上探究结果,我们可以得到:
非负数都有算术平方根,
算术平方根都是非负数 .
归纳与概括
∣揭示本质的属性
算术平方根用符号表示如下
如果 x2=a(x≥0),则x= .
a的算术平方根记作 ,读作“根号a”,
a叫做被开方数。
填空:
1.16的算术平方根用符号表示为
2.100的算术平方根用符号表示为
4. 符号 表示的意义为
5. 符号 表示的意义为
学以致用
6. 符号 表示的意义为
3.2的算术平方根用符号表示为
25的算术平方根
17的算术平方根
的算术平方根
∣加深对概念的理解
巩固与应用
(1)求下列各数的算术平方根.
① 144 ②
③ 32
(2)求下列各式的值.
① ② ③
=0.3
=
=2
计算:
解:因为 =144,
所以 =12.
解:因为 = ,
所以 =3.
解:因为 = ,
所以 = .
回 顾 与 反 思
——让我们的认识升华
这节课我们学习了什么数学概念?
我们获得这个概念,经历了怎样的过程?
通过这个过程,你有什么感受和体会?
根据你对算术平方根的理解,
现在你能解释 的意义吗?
2
本节作业
课本p69练习题第1,2题
必做题:
试探究非负数a与a的算术平方根的大小关系.
选做题:
