矩形的性质
图片预览




文档简介
(共28张PPT)
19.2.1 矩 形
知识目标:
探索矩形与平行四边形的关系,掌握矩形的有关性质及推论 ,并能用它们解决简单的问题.
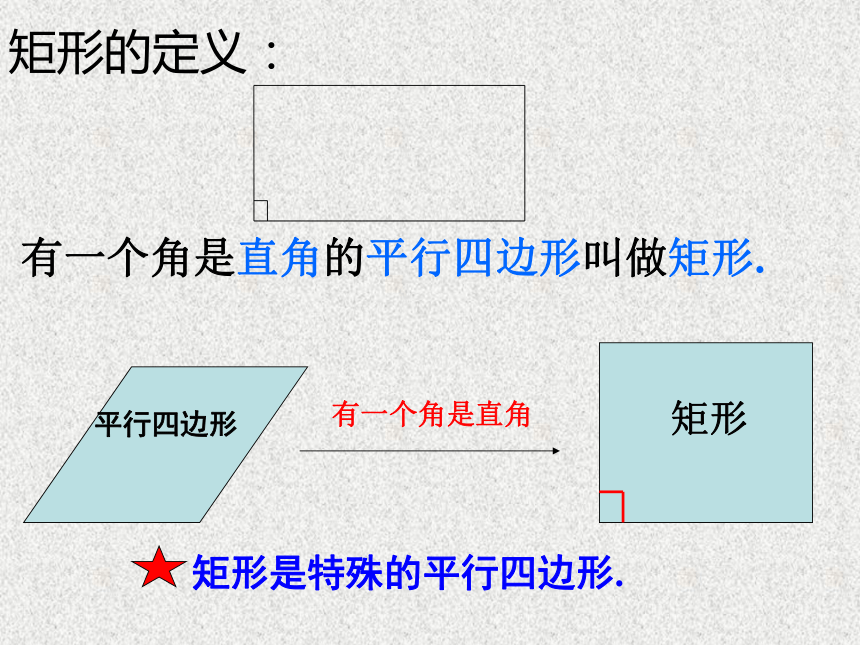
矩形的定义:
矩形的定义:
平行四边形
矩形
有一个角是直角
矩形是特殊的平行四边形.
有一个角是直角的平行四边形叫做矩形.
2. 平行四边形是矩形. ( )
判断下列句子是否正确.
1. 矩形是平行四边形.( )
正确
错误
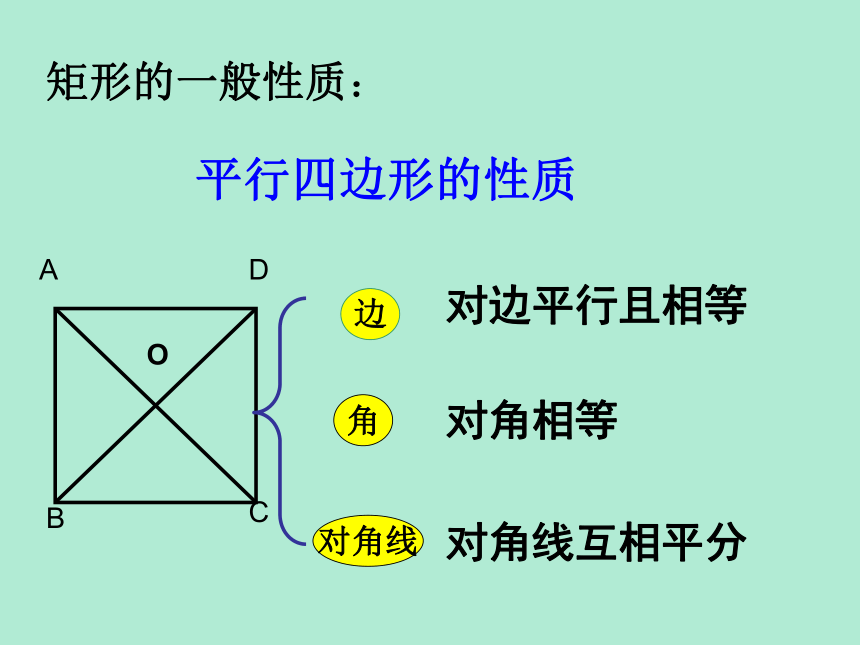
平行四边形的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:
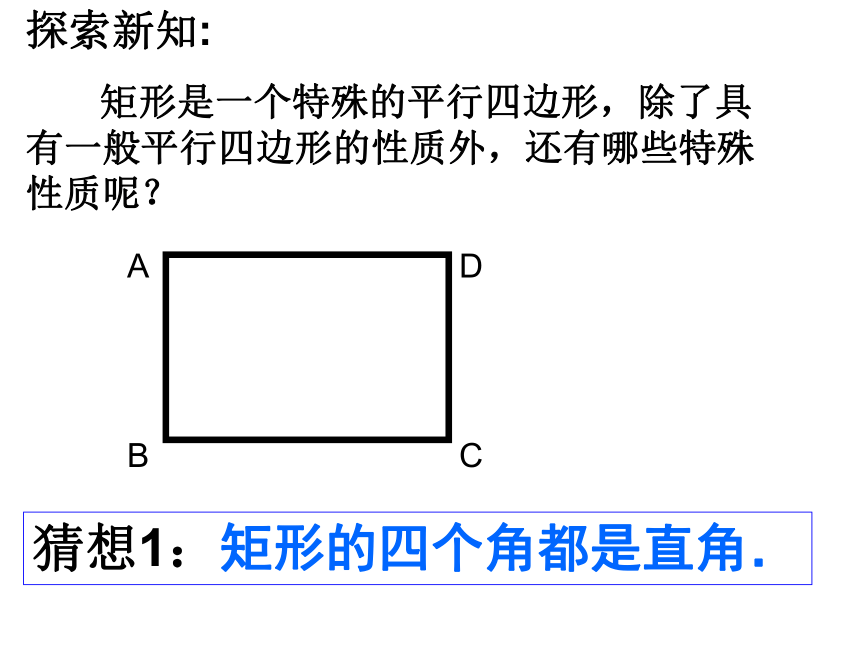
探索新知:
矩形是一个特殊的平行四边形,除了具有一般平行四边形的性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
A
B
C
D
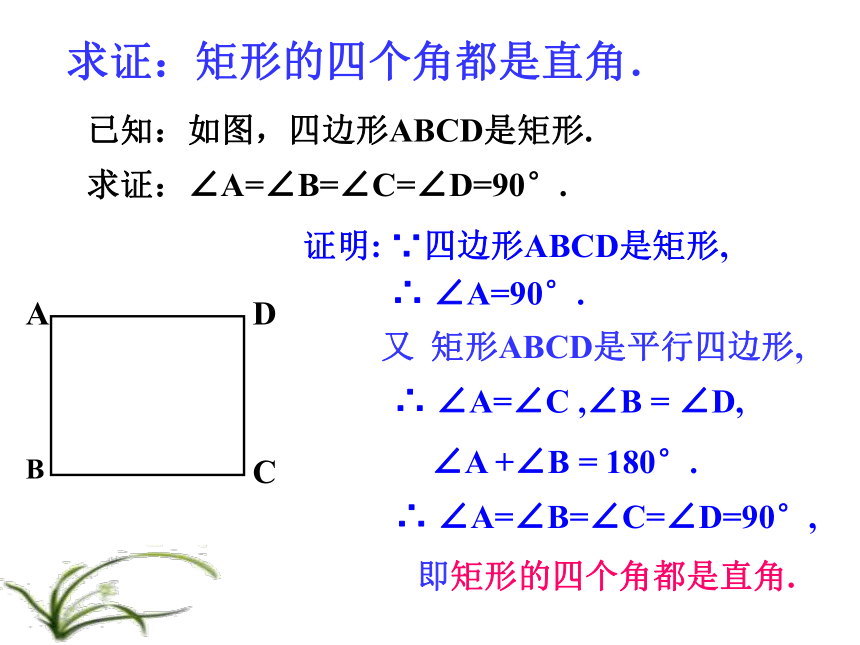
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又 矩形ABCD是平行四边形,
∴ ∠A=∠C ,∠B = ∠D,
∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
探索新知:
矩形是一个特殊的平行四边形,除了具有一般平行四边形的所有性质外,还有哪些特殊性质呢?
性质1:矩形的四个角都是直角.
A
B
C
D
猜想2:矩形的对角线相等.
已知:如图,四边形ABCD是矩形.
求证:AC = DB.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠ABC = ∠DCB = 90°.
又∵AB = DC , BC = CB,
∴△ABC≌△DCB (SAS).
∴AC = DB 即矩形的对角线相等.
求证:矩形的对角线相等.
(从而得到OA=OC=OB=OD= AC= BD)
O
矩形特殊的性质
矩形的四个角都是直角.
1.从角上看:
数学语言:
2.从对角线上看:矩形的对角线相等.
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
∵四边形ABCD是矩形, ∴AC = BD.
数学语言:
A
O
B
C
D
矩形的对角线互相平分
矩形的对边相等
矩形的对边平行
矩形的四个角都是直角
矩形的对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD=BC ,AB=CD
∴AD∥BC ,AB∥CD
∴AC= BD
A
B
C
D
O
∴OA=OC ,OB=OD
★ 矩形是轴对称图形.
★ 矩形的对角线将矩形分 - -成四个等腰三角形.
(OA=OC=OB=OD= AC= BD)
设矩形的对角线AC与BD交于点O,那么BO是Rt△ABC中一条怎样的特殊线段
它与AC有什么大小关系
D
B
C
A
O
由此可得推论:
直角三角形斜边上的中线
等于斜边的一半.
BO是Rt△ABC中斜边AC上的中线.
BO等于AC的一半.
议一议:
第十九章 四边形
OA=OC=OB=OD= AC= BD
推论(直角三角形的一个性质):
直角三角形斜边上的中线等于斜边的一半.
数学语言:∵在Rt△ABC中,BO是斜边AC上的中线,
A
B
C
O
∴BO= AC.
方法小结: 如果矩形两对角线的夹角是60°或120°,
则其中必有等边三角形.
∴AC与BD相等且互相平分,
∴ OA=OB.
∵ ∠AOB=60°,
∴ △AOB是等边三角形,
∴ OA=AB=4㎝.
∴ 矩形的对角线长 AC=BD=2OA=8㎝.
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
例1 如图,矩形ABCD的两条对角线相交于点O, ∠AOB=60°,AB=4㎝,求矩形对角线的长.
如果矩形的一条对角线长为4 cm,两条对角线的一个交角为120°,求矩形的边长(精确到0.1cm).
A
B
O
C
D
AB=CD≈3.5 cm
AD=BC=6 cm
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的 中线等于斜边的一半.
矩形定义:有一个角是直角的平行四边形叫做矩形.
点击进入
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD.
1.矩形具有而一般平行四边形不具有的性质( )
A.内角和是360° B.对角相等
C.对边平行且相等 D.对角线相等
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直
D
D
课堂练习
3.矩形和平行四边形都具有的性质是( )
A.邻角相等 B.对角线互相垂直
C.邻角互补 D.对角线相等
C
课堂练习
4. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为 ( )
A. 50° B. 60° C. 70° D. 80°
5. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于( )
A. 30° B. 45° C. 60° D. 120°
D
A
40°
A
B
C
D
O
D
C
A
B
E
填一填
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=___㎝ , OB=____㎝;
2.若已知∠DOC=120°,AC=8㎝,
则AD= ____cm,AB= _____cm.
O
D
C
B
A
10
5
4
D
C
B
A
┓
3.如图,已知在Rt△ABC中,∠ABC=90°,
BD是斜边AC上的中线.
(1)若BD=3㎝ ,则AC= ㎝;
若∠C=30°, AB=5㎝,
则AC= ㎝, BD= ㎝.
6
5
10
图中寻宝
试一试
给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理.
作 业
课本P102 第4题
19.2.1 矩 形
知识目标:
探索矩形与平行四边形的关系,掌握矩形的有关性质及推论 ,并能用它们解决简单的问题.
矩形的定义:
矩形的定义:
平行四边形
矩形
有一个角是直角
矩形是特殊的平行四边形.
有一个角是直角的平行四边形叫做矩形.
2. 平行四边形是矩形. ( )
判断下列句子是否正确.
1. 矩形是平行四边形.( )
正确
错误
平行四边形的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:
探索新知:
矩形是一个特殊的平行四边形,除了具有一般平行四边形的性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
A
B
C
D
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又 矩形ABCD是平行四边形,
∴ ∠A=∠C ,∠B = ∠D,
∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
探索新知:
矩形是一个特殊的平行四边形,除了具有一般平行四边形的所有性质外,还有哪些特殊性质呢?
性质1:矩形的四个角都是直角.
A
B
C
D
猜想2:矩形的对角线相等.
已知:如图,四边形ABCD是矩形.
求证:AC = DB.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠ABC = ∠DCB = 90°.
又∵AB = DC , BC = CB,
∴△ABC≌△DCB (SAS).
∴AC = DB 即矩形的对角线相等.
求证:矩形的对角线相等.
(从而得到OA=OC=OB=OD= AC= BD)
O
矩形特殊的性质
矩形的四个角都是直角.
1.从角上看:
数学语言:
2.从对角线上看:矩形的对角线相等.
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
∵四边形ABCD是矩形, ∴AC = BD.
数学语言:
A
O
B
C
D
矩形的对角线互相平分
矩形的对边相等
矩形的对边平行
矩形的四个角都是直角
矩形的对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD=BC ,AB=CD
∴AD∥BC ,AB∥CD
∴AC= BD
A
B
C
D
O
∴OA=OC ,OB=OD
★ 矩形是轴对称图形.
★ 矩形的对角线将矩形分 - -成四个等腰三角形.
(OA=OC=OB=OD= AC= BD)
设矩形的对角线AC与BD交于点O,那么BO是Rt△ABC中一条怎样的特殊线段
它与AC有什么大小关系
D
B
C
A
O
由此可得推论:
直角三角形斜边上的中线
等于斜边的一半.
BO是Rt△ABC中斜边AC上的中线.
BO等于AC的一半.
议一议:
第十九章 四边形
OA=OC=OB=OD= AC= BD
推论(直角三角形的一个性质):
直角三角形斜边上的中线等于斜边的一半.
数学语言:∵在Rt△ABC中,BO是斜边AC上的中线,
A
B
C
O
∴BO= AC.
方法小结: 如果矩形两对角线的夹角是60°或120°,
则其中必有等边三角形.
∴AC与BD相等且互相平分,
∴ OA=OB.
∵ ∠AOB=60°,
∴ △AOB是等边三角形,
∴ OA=AB=4㎝.
∴ 矩形的对角线长 AC=BD=2OA=8㎝.
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
例1 如图,矩形ABCD的两条对角线相交于点O, ∠AOB=60°,AB=4㎝,求矩形对角线的长.
如果矩形的一条对角线长为4 cm,两条对角线的一个交角为120°,求矩形的边长(精确到0.1cm).
A
B
O
C
D
AB=CD≈3.5 cm
AD=BC=6 cm
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的 中线等于斜边的一半.
矩形定义:有一个角是直角的平行四边形叫做矩形.
点击进入
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD.
1.矩形具有而一般平行四边形不具有的性质( )
A.内角和是360° B.对角相等
C.对边平行且相等 D.对角线相等
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直
D
D
课堂练习
3.矩形和平行四边形都具有的性质是( )
A.邻角相等 B.对角线互相垂直
C.邻角互补 D.对角线相等
C
课堂练习
4. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为 ( )
A. 50° B. 60° C. 70° D. 80°
5. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于( )
A. 30° B. 45° C. 60° D. 120°
D
A
40°
A
B
C
D
O
D
C
A
B
E
填一填
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=___㎝ , OB=____㎝;
2.若已知∠DOC=120°,AC=8㎝,
则AD= ____cm,AB= _____cm.
O
D
C
B
A
10
5
4
D
C
B
A
┓
3.如图,已知在Rt△ABC中,∠ABC=90°,
BD是斜边AC上的中线.
(1)若BD=3㎝ ,则AC= ㎝;
若∠C=30°, AB=5㎝,
则AC= ㎝, BD= ㎝.
6
5
10
图中寻宝
试一试
给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理.
作 业
课本P102 第4题
