21.2.3 解一元二次方程 因式分解法 课时达标检测(含解析)
文档属性
| 名称 | 21.2.3 解一元二次方程 因式分解法 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 07:04:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年九年级上册数学同步练习卷
21.2解一元二次方程
21.2.3 因式分解法
一、单选题
1.方程的根是( )
A. B.
C. D.
2.分式方程的解为( )
A. B. C.或 D.
3.如果(x﹣y﹣2)(x﹣y+1)=0,那么x﹣y=( )
A.2 B.﹣1 C.2或﹣1 D.﹣2或1
4.对于实数a、b定义新运算“”如下:,如,,若一元二次方程的两根为 (),则的 结果是( )
A. B. C. D.2
5.对于实数m,n,先定义一种新运算“?”如下:m?n=,若x?(﹣2)=10,则实数x等于( )
A.3 B.﹣4 C.8 D.3或8
6.已知关于的一元二次方程有两个不相等的实数根,若为非负整数,且该方程的根都是整数,则的值为( )
A.1 B.0 C.0或1 D.
7.如图是清朝李演撰写的《九章算术细草图说》中的“勾股圆方图",四边形ABCD,四边形EBGF,四边形HNQD均为正方形,BG,NQ,BC是某个直角三角形的三边,其中BC是斜边,若,则AB的长为( )
A. B. C.3 D.
8.方程的解是( )
A.2或0 B.±2或0 C.2 D.-2或0
9.如图,在矩形ABCD中,AB=14,BC=7,M、N分别为AB、CD的中点,P、Q均为CD边上的动点(点Q在点P左侧),点G为MN上一点,且PQ=NG=5,则当MP+GQ=13时,满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
10.若,,,,为互不相等的正奇数,满足
,则的末位数字是( )
A.1 B.3 C.5 D.7
11.下面一元二次方程的解法中,正确的是(?? ?).
A. ,∴ x-3=10,x-5=2,∴ ;
B. ,∴ ,∴ ;
C. ,∴ ;
D.两边同除以x,得x=1.
12. 因式分解结果为(???? )
A.
B.
C.
D. ?
二、填空题
13.方程x2﹣2x=0的根是_____.
14.已知是方程的解,求_____________.
15.数学活动课上,小云和小王在讨论张老师出示的一道代数式求值问题:
已知实数同时满足,求代数式的值.
结合他们的对话,请解答下列问题:
(1)当时,a的值是__________.
(2)当时,代数式的值是__________.
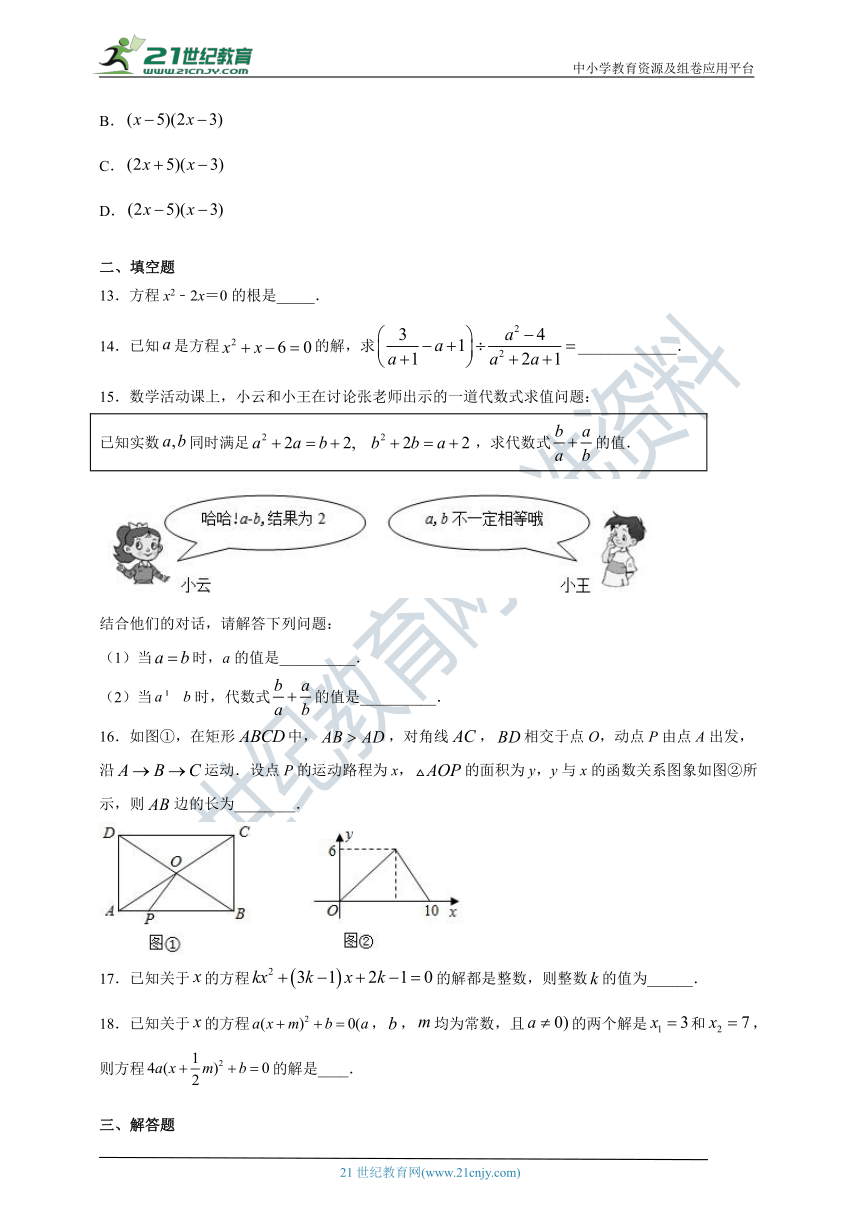
16.如图①,在矩形中,,对角线,相交于点O,动点P由点A出发,沿运动.设点P的运动路程为x,的面积为y,y与x的函数关系图象如图②所示,则边的长为________.
17.已知关于的方程的解都是整数,则整数的值为______.
18.已知关于的方程,,均为常数,且的两个解是和,则方程的解是____.
三、解答题
19.解方程(x﹣1)(x+2)=2(x+2).
解方程:(2x﹣1)2=3x2+6.
21.已知关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围;
(2)请你给出一个的值,并求出此时方程的根.
22.先化简,再求值:
,其中x满足.
23.已知,,为有理数,且多项式能够写成的形式.
(1)求的值.
(2)求的值.
(3)若,,为整数,且,试求,,的值.
参考答案
1.C
【详解】
解:∵,
∴,
∴,
∴x+7=0,x-8=0,
∴x1=-7,x2=8.
2.A
【详解】
解:,
去分母得:2(x+2)+x2?4=8,
解得:x=2或x=?4,
检验:当x=2时,(x+2)(x?2)=0,
当x=?4时,(x+2)(x?2)≠0,
∴x=2是增根,分式方程的解为x=?4.
3.C
【详解】
解:
或
或
4.C
【详解】
解:方程变形得:,
∵
∴解得:,,
∴
5.A
【分析】
分和两种情况,分别可得一个关于的方程,解方程即可得.
【详解】
解:由题意,分以下两种情况:
(1)当时,
则,即,
解得或(舍去);
(2)当时,
则,即,
解得(舍去);
综上,
6.A
【详解】
解:∵一元二次方程x2-2x+m-1=0有两个不相等的实数根,
∴△=(-2)2-4×1×(m-1)>0,
∴m<2;
∵m为非负整数,
∴m=0或1,
当m=0时,x2-2x-1=0,
∵△=(-2)2-4×1×(-1)=8,
∴,
此时方程的根不是整数,
∴m=0舍去;
当m=1时,x2-2x=0,
∴,此时方程的根都是整数,
∴m=1,
故选:A.
7.B
【详解】
解:∵四边形ABCD,四边形EBGF,四边形HNQD均为正方形,,
∴,四边形AEMH是矩形,
∴AH=EM,HM=AE,
∵,
∴,
由可设,
∴,
∴,
∵BG,NQ,BC是某个直角三角形的三边,
∴,即,
解得:(不符合题意,舍去),
∴;
8.B
【详解】
.解:∵,
∴,
∴或或,
9.D
【详解】
解:如图,当在的两侧时,设 则
矩形ABCD,M、N分别为AB、CD的中点,
四边形 四边形都是矩形,
由勾股定理得:
整理得:
如图,当在的右侧时,设
同理可得:
解得: 不合题意舍去,
如图,当都在的左侧时,设
同理可得:
解得: 不合题意舍去,
10.A
【详解】
解:∵,,,,为互不相等的正奇数
∴,,,,为互不相等的偶数,且负数个数为偶数个
而将分解为5个互不相等的偶数之积,只有唯一的形式:
∴,,,,分别等于2、、4、6、
∴,,,,分别等于2007,2003,2001,1999,2011
又∵20072尾数是9,20032尾数是9,20012尾数是1,19992尾数是1,20112尾数是1
∴的末位数字是1.
11.B
【解析】
A 的方程解法是错误的,应该为:(x-3)(x-5)=10×2,化简可得-8x-5=0,然后利用求根公式进行解答;
C的方程的解法也是错误的,应该为:整理为+4=0,即:=-4,由于任何数的平方都是非负数,故方程无解;
D的解法也是错误的,应改为:-x=0,解得:x=0或x=1.
故选:B.
12.D
【解析】
根据因式分解的方法,可提公因式(x-3)为:(x-3)(2x-5).
故选:D.
点睛:此题主要考查了因式分解,因式分解是把一个多项式化为几个因式积的形式.根据因式分解的一般步骤:一提(公因式)、二套(平方差公式,完全平方公式)、三检查(彻底分解).
13.x1=0,x2=2
【详解】
解:因式分解得x(x﹣2)=0,
x=0或x﹣2=0
∴x1=0,x2=2.
故答案为x1=0,x2=2.
14.2
【详解】
解:
=
=
=
=
∵是方程的解,
∴,
∴,
解得:a=2或a=-3,
∵a≠2,
∴当a=-3时,原式=-(-3)-1=2,
故答案为:2.
15.或1 7
【详解】
解:已知,实数,同时满足①,②,
①-②得,
∴
∴或
①+②得,
(1)当时,将代入得,
解得,,
∴,
把代入得,3=3,成立;
把代入得,0=0,成立;
∴当时,a的值是1或-2
故答案为:1或-2;
(2)当时,则,即
∵
∴
∴
∴
∴
16.6
【详解】
如图,过点O作OM⊥AB,垂足为M,
∵四边形ABCD是矩形,
∴OD=OB,DA⊥AB,AD=BC,
∵OM⊥AB,
∴OM∥AB,AM=BM,
∴OM=,结合图像知,当运动到点B是三角形的面积最大,
∴即AD×AB=24,当点P运动到点C时,面积为0即AB+BC=10,
∴AD+AB=10,
∴AB,AD是方程的两个根,
解得x=4或x=6,
∵,
∴AB=6,
故答案为:6.
17.0或1或
【详解】
由题意,分以下两种情况:
(1)当时,
方程为,解得,满足解是整数;
(2)当时,
方程为一元二次方程,
因式分解,得,
解得,
方程的解都是整数,k也是整数,
一定是整数,
整数或;
综上,整数的值为0或1或,
故答案为:0或1或.
【点睛】
本题考查了解一元一次方程、解一元二次方程,熟练掌握一元二次方程的解法是解题关键.
18.,
【分析】
先根据题意得出或,再将变形为:,进而根据或计算即得.
【详解】
∵关于的方程,,均为常数,且的两个解是和
∴或
∵
∴
∴或
∴或
故答案为:,
19.x1=﹣2,x2=3
【分析】
把右边的项移到左边,用提公因式法因式分解可以求出方程的根.
【详解】
解:(x﹣1)(x+2)﹣2(x+2)=0,
(x+2)(x﹣1﹣2)=0,
(x+2)(x﹣3)=0,
∴x+2=0,x﹣3=0,
解得x1=﹣2,x2=3.
20.
【详解】
解:
化简得:
因式分解得:
所以,.
21.(1)k>0 ;(2)k=1;x1=0,x2=2
【详解】
解:(1)∵关于x的一元二次方程x2-2x+1-k=0有两个不相等的实数根.
∴△=(-2)2-4×1×(1-k)>0,
解得k>0;
(2)由(1)知,实数k的取值范围为k>0,
故取k=1,
则x2-2x=0,即x(x-2)=0,
解得,x1=0,x2=2.
22.x(x+1);6
【详解】
解:∵
∴x=2或x=-1
∴
=
=
=
=x(x+1)
∵x=-1分式无意义,∴x=2
当x=2时,x(x+1)=2×(2+1)=6.
23.(1);(2);(3),,.
【详解】
(1)是的一个因式,
,即,是方程的解,
,
得:③,
.
(2)由③得:④,
④代入①得:⑤,
.
(3),
,
,
解得:,
又,均为大于的整数,
可取的值有,,,,,
又为正整数,
,,
则,
,,.
_21?????????è?????(www.21cnjy.com)_
人教版2021年九年级上册数学同步练习卷
21.2解一元二次方程
21.2.3 因式分解法
一、单选题
1.方程的根是( )
A. B.
C. D.
2.分式方程的解为( )
A. B. C.或 D.
3.如果(x﹣y﹣2)(x﹣y+1)=0,那么x﹣y=( )
A.2 B.﹣1 C.2或﹣1 D.﹣2或1
4.对于实数a、b定义新运算“”如下:,如,,若一元二次方程的两根为 (),则的 结果是( )
A. B. C. D.2
5.对于实数m,n,先定义一种新运算“?”如下:m?n=,若x?(﹣2)=10,则实数x等于( )
A.3 B.﹣4 C.8 D.3或8
6.已知关于的一元二次方程有两个不相等的实数根,若为非负整数,且该方程的根都是整数,则的值为( )
A.1 B.0 C.0或1 D.
7.如图是清朝李演撰写的《九章算术细草图说》中的“勾股圆方图",四边形ABCD,四边形EBGF,四边形HNQD均为正方形,BG,NQ,BC是某个直角三角形的三边,其中BC是斜边,若,则AB的长为( )
A. B. C.3 D.
8.方程的解是( )
A.2或0 B.±2或0 C.2 D.-2或0
9.如图,在矩形ABCD中,AB=14,BC=7,M、N分别为AB、CD的中点,P、Q均为CD边上的动点(点Q在点P左侧),点G为MN上一点,且PQ=NG=5,则当MP+GQ=13时,满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
10.若,,,,为互不相等的正奇数,满足
,则的末位数字是( )
A.1 B.3 C.5 D.7
11.下面一元二次方程的解法中,正确的是(?? ?).
A. ,∴ x-3=10,x-5=2,∴ ;
B. ,∴ ,∴ ;
C. ,∴ ;
D.两边同除以x,得x=1.
12. 因式分解结果为(???? )
A.
B.
C.
D. ?
二、填空题
13.方程x2﹣2x=0的根是_____.
14.已知是方程的解,求_____________.
15.数学活动课上,小云和小王在讨论张老师出示的一道代数式求值问题:
已知实数同时满足,求代数式的值.
结合他们的对话,请解答下列问题:
(1)当时,a的值是__________.
(2)当时,代数式的值是__________.
16.如图①,在矩形中,,对角线,相交于点O,动点P由点A出发,沿运动.设点P的运动路程为x,的面积为y,y与x的函数关系图象如图②所示,则边的长为________.
17.已知关于的方程的解都是整数,则整数的值为______.
18.已知关于的方程,,均为常数,且的两个解是和,则方程的解是____.
三、解答题
19.解方程(x﹣1)(x+2)=2(x+2).
解方程:(2x﹣1)2=3x2+6.
21.已知关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围;
(2)请你给出一个的值,并求出此时方程的根.
22.先化简,再求值:
,其中x满足.
23.已知,,为有理数,且多项式能够写成的形式.
(1)求的值.
(2)求的值.
(3)若,,为整数,且,试求,,的值.
参考答案
1.C
【详解】
解:∵,
∴,
∴,
∴x+7=0,x-8=0,
∴x1=-7,x2=8.
2.A
【详解】
解:,
去分母得:2(x+2)+x2?4=8,
解得:x=2或x=?4,
检验:当x=2时,(x+2)(x?2)=0,
当x=?4时,(x+2)(x?2)≠0,
∴x=2是增根,分式方程的解为x=?4.
3.C
【详解】
解:
或
或
4.C
【详解】
解:方程变形得:,
∵
∴解得:,,
∴
5.A
【分析】
分和两种情况,分别可得一个关于的方程,解方程即可得.
【详解】
解:由题意,分以下两种情况:
(1)当时,
则,即,
解得或(舍去);
(2)当时,
则,即,
解得(舍去);
综上,
6.A
【详解】
解:∵一元二次方程x2-2x+m-1=0有两个不相等的实数根,
∴△=(-2)2-4×1×(m-1)>0,
∴m<2;
∵m为非负整数,
∴m=0或1,
当m=0时,x2-2x-1=0,
∵△=(-2)2-4×1×(-1)=8,
∴,
此时方程的根不是整数,
∴m=0舍去;
当m=1时,x2-2x=0,
∴,此时方程的根都是整数,
∴m=1,
故选:A.
7.B
【详解】
解:∵四边形ABCD,四边形EBGF,四边形HNQD均为正方形,,
∴,四边形AEMH是矩形,
∴AH=EM,HM=AE,
∵,
∴,
由可设,
∴,
∴,
∵BG,NQ,BC是某个直角三角形的三边,
∴,即,
解得:(不符合题意,舍去),
∴;
8.B
【详解】
.解:∵,
∴,
∴或或,
9.D
【详解】
解:如图,当在的两侧时,设 则
矩形ABCD,M、N分别为AB、CD的中点,
四边形 四边形都是矩形,
由勾股定理得:
整理得:
如图,当在的右侧时,设
同理可得:
解得: 不合题意舍去,
如图,当都在的左侧时,设
同理可得:
解得: 不合题意舍去,
10.A
【详解】
解:∵,,,,为互不相等的正奇数
∴,,,,为互不相等的偶数,且负数个数为偶数个
而将分解为5个互不相等的偶数之积,只有唯一的形式:
∴,,,,分别等于2、、4、6、
∴,,,,分别等于2007,2003,2001,1999,2011
又∵20072尾数是9,20032尾数是9,20012尾数是1,19992尾数是1,20112尾数是1
∴的末位数字是1.
11.B
【解析】
A 的方程解法是错误的,应该为:(x-3)(x-5)=10×2,化简可得-8x-5=0,然后利用求根公式进行解答;
C的方程的解法也是错误的,应该为:整理为+4=0,即:=-4,由于任何数的平方都是非负数,故方程无解;
D的解法也是错误的,应改为:-x=0,解得:x=0或x=1.
故选:B.
12.D
【解析】
根据因式分解的方法,可提公因式(x-3)为:(x-3)(2x-5).
故选:D.
点睛:此题主要考查了因式分解,因式分解是把一个多项式化为几个因式积的形式.根据因式分解的一般步骤:一提(公因式)、二套(平方差公式,完全平方公式)、三检查(彻底分解).
13.x1=0,x2=2
【详解】
解:因式分解得x(x﹣2)=0,
x=0或x﹣2=0
∴x1=0,x2=2.
故答案为x1=0,x2=2.
14.2
【详解】
解:
=
=
=
=
∵是方程的解,
∴,
∴,
解得:a=2或a=-3,
∵a≠2,
∴当a=-3时,原式=-(-3)-1=2,
故答案为:2.
15.或1 7
【详解】
解:已知,实数,同时满足①,②,
①-②得,
∴
∴或
①+②得,
(1)当时,将代入得,
解得,,
∴,
把代入得,3=3,成立;
把代入得,0=0,成立;
∴当时,a的值是1或-2
故答案为:1或-2;
(2)当时,则,即
∵
∴
∴
∴
∴
16.6
【详解】
如图,过点O作OM⊥AB,垂足为M,
∵四边形ABCD是矩形,
∴OD=OB,DA⊥AB,AD=BC,
∵OM⊥AB,
∴OM∥AB,AM=BM,
∴OM=,结合图像知,当运动到点B是三角形的面积最大,
∴即AD×AB=24,当点P运动到点C时,面积为0即AB+BC=10,
∴AD+AB=10,
∴AB,AD是方程的两个根,
解得x=4或x=6,
∵,
∴AB=6,
故答案为:6.
17.0或1或
【详解】
由题意,分以下两种情况:
(1)当时,
方程为,解得,满足解是整数;
(2)当时,
方程为一元二次方程,
因式分解,得,
解得,
方程的解都是整数,k也是整数,
一定是整数,
整数或;
综上,整数的值为0或1或,
故答案为:0或1或.
【点睛】
本题考查了解一元一次方程、解一元二次方程,熟练掌握一元二次方程的解法是解题关键.
18.,
【分析】
先根据题意得出或,再将变形为:,进而根据或计算即得.
【详解】
∵关于的方程,,均为常数,且的两个解是和
∴或
∵
∴
∴或
∴或
故答案为:,
19.x1=﹣2,x2=3
【分析】
把右边的项移到左边,用提公因式法因式分解可以求出方程的根.
【详解】
解:(x﹣1)(x+2)﹣2(x+2)=0,
(x+2)(x﹣1﹣2)=0,
(x+2)(x﹣3)=0,
∴x+2=0,x﹣3=0,
解得x1=﹣2,x2=3.
20.
【详解】
解:
化简得:
因式分解得:
所以,.
21.(1)k>0 ;(2)k=1;x1=0,x2=2
【详解】
解:(1)∵关于x的一元二次方程x2-2x+1-k=0有两个不相等的实数根.
∴△=(-2)2-4×1×(1-k)>0,
解得k>0;
(2)由(1)知,实数k的取值范围为k>0,
故取k=1,
则x2-2x=0,即x(x-2)=0,
解得,x1=0,x2=2.
22.x(x+1);6
【详解】
解:∵
∴x=2或x=-1
∴
=
=
=
=x(x+1)
∵x=-1分式无意义,∴x=2
当x=2时,x(x+1)=2×(2+1)=6.
23.(1);(2);(3),,.
【详解】
(1)是的一个因式,
,即,是方程的解,
,
得:③,
.
(2)由③得:④,
④代入①得:⑤,
.
(3),
,
,
解得:,
又,均为大于的整数,
可取的值有,,,,,
又为正整数,
,,
则,
,,.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
