21.3 实际问题与一元二次方程 课时达标检测(含解析)
文档属性
| 名称 | 21.3 实际问题与一元二次方程 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 21:47:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年九年级上册数学同步练习卷
21.3 实际问题与一元二次方程
一、单选题
1.主题为“绿色城市、健康生活”的世界园艺博览会将于2021年4月至10月在枣林湾举行.世园会的某纪念品受到热烈欢迎,从原价50元连续两次涨价达到72元,如果每次涨价的百分率都是x,则下面所列方程正确的是( )
A. B.
C. D.
2.如图,把一块长为50cm,宽为40cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为400cm2,设剪去小正方形的边长为xcm,则可列方程为( )
A. B.
C. D.
3.某商品连续两次降价,每件零售价由原来的56元降到了31.5元,若设平均每次降价的百分率为,则可列方程为( )
A. B.
C. D.
4.若比与的积小1,则关于的值,下列说法正确的是( )
A.不存在这样的值 B.有两个相等的的值
C.有两个不相等的的值 D.无法确定
5.用总长的铝合金材料做一个如图所示的窗框(不计损耗),窗框的上部是等腰直角三角形,下部是一个矩形,窗框的总面积为(材料的厚度忽略不计).若设等腰直角三角形的斜边长为,则下列方程符合题意的是( ).
A. B.
C. D.
6.如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
A. B. C. D.
7.某班学生毕业时,每一位同学都向全班其他同学送一张自己的相片作为纪念,全班共送了2550张相片,若设全班有名学生,则可列方程为( )
A. B.
C. D.
8.如图①,在矩形中,,对角线,相交于点,动点由点出发,沿向点运动.设点的运动路程为,的面积为,与的函数关系图象如图②所示,则对角线的长为( )
A.3 B.4 C.5 D.6
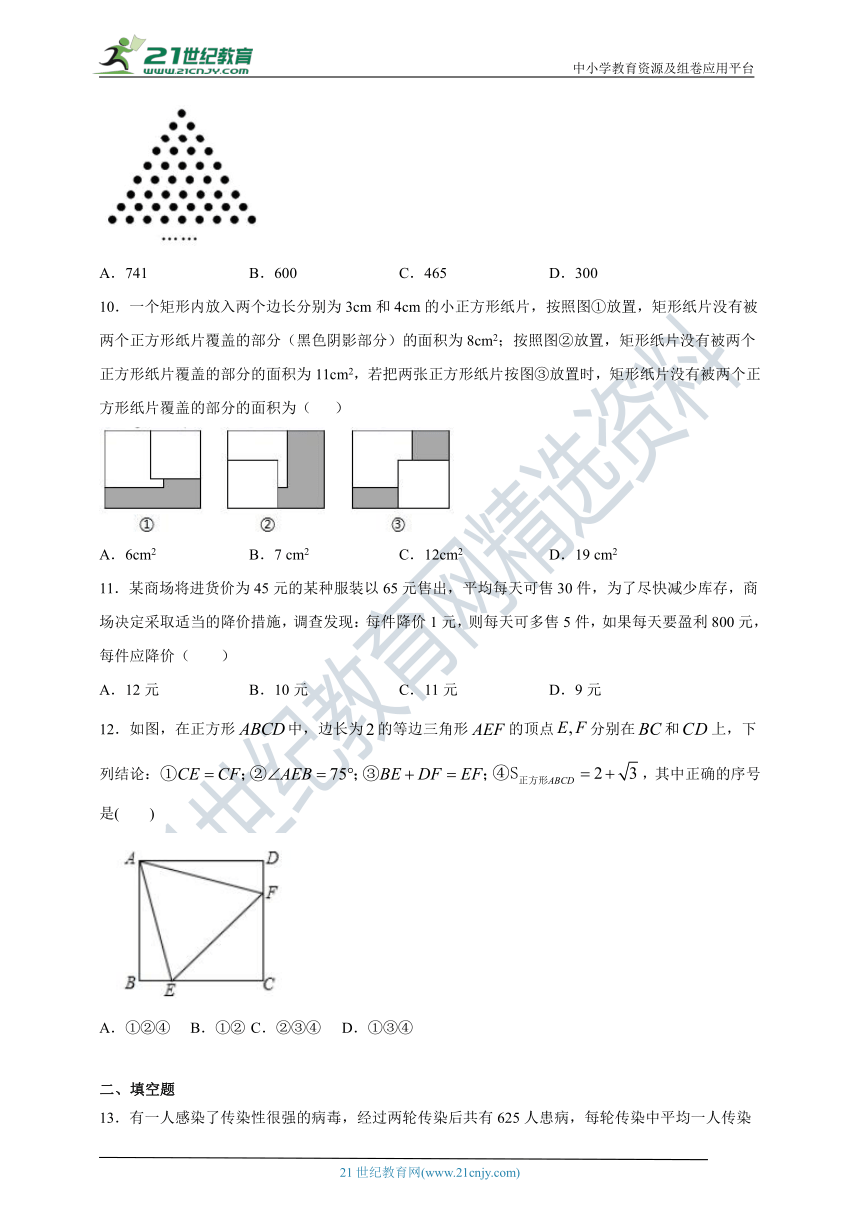
9.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第行有个点…,前行的点数和不能是以下哪个结果 ( )
A.741 B.600 C.465 D.300
10.一个矩形内放入两个边长分别为3cm和4cm的小正方形纸片,按照图①放置,矩形纸片没有被两个正方形纸片覆盖的部分(黑色阴影部分)的面积为8cm2;按照图②放置,矩形纸片没有被两个正方形纸片覆盖的部分的面积为11cm2,若把两张正方形纸片按图③放置时,矩形纸片没有被两个正方形纸片覆盖的部分的面积为( )
A.6cm2 B.7 cm2 C.12cm2 D.19 cm2
11.某商场将进货价为45元的某种服装以65元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价( )
A.12元 B.10元 C.11元 D.9元
12.如图,在正方形中,边长为的等边三角形的顶点分别在和上,下列结论:,其中正确的序号是( )
A.①②④ B.①② C.②③④ D.①③④
二、填空题
13.有一人感染了传染性很强的病毒,经过两轮传染后共有625人患病,每轮传染中平均一人传染______人.
14.新能源汽车节能环保,越来越受到消费者的喜爱,各种品牌相继投放市场.某地2018年新能源汽车的销售量为50.7万辆,销售量逐年增加,到2020年为125.6万辆.若年增长率x不变,则x的值是多少?根据题意可列方程为_________.
15.劳动教育己纳入人才培养全过程,某学校加大投入,建设校园农场,该农场一种作物的产量两年内从300千克增加到363千克.设平均每年增产的百分率为,则可列方程为________.
16.在中,,厘米,厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过______秒后,P,Q两点间距离为厘米.
17.观察下列图形,第1个图形中一共有4个小圆圈,第2个图形中一共有10个小圆圈,第3个图形中一共有18个小圆圈,…,第_____个图形中一共有54个小圆圈……按此规律排列,则第n个图形中小圆圈的个数是___________.
18.已知:如图,等腰直角,,,点D为外一点,,连接CD,,,BC的长为________.
三、解答题
19.如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.
(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由.
20.突如其来的新冠疫情影响了某商场的经济效益,在复工复产后商场对某种商品价格进行了调整,将该种商品的进价提高了8元定为销售价格,此时该商品8件的进价恰好相当于6件的售价,且每天可售出200件.经市场调查发现:如果该商品每件再涨价1元,每天就会少售出5件.
(1)该商品的售价和进价各是多少元?
(2)若在进价不变的条件下,确保每天所得的销售利润为2035元,且销售量尽可能大,则该商品应再涨价多少元?
21.苏科版九上数学p31阅读《各类方程的解法》中提到:各类方程的解法不尽相同,但是它们有一个共同的基本数学思想﹣﹣转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= ;
(2)用“转化”思想求方程=x的解;
(3)拓展:若实数x满足x2+=2,求x+的值
22.2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
23.Rt△ABC中,∠ACB=90°,AC=BC=6,动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动,到达点C停止运动.设运动时间为t秒
(1)如图1,过点P作PD⊥AC,交AB于D,若△PBC与△PAD的面积和是△ABC的面积的,求t的值;
(2)点Q在射线PC上,且PQ=2AP,以线段PQ为边向上作正方形PQNM.在运动过程中,若设正方形PQNM与△ABC重叠部分的面积为8,求t的值.
参考答案
1.D
【详解】
解:每次涨价的百分率都是,则第一次涨价后价格为元,第二次涨价后价格为
所以
2.B
【详解】
根据题意,底面矩形的长为:,宽为:,根据题意得:
3.A
【详解】
设平均每次降价的百分率为
第一次降价后的价格为:
第二次降价后的价格为:
∴可列方程
4.C
【详解】
解:由题意,得,
整理得,
∵,
∴方程有两个不相等的实数根,
即,,
5.D
【详解】
解:设等腰直角三角形的斜边长为,则等腰直角三角形的直角边长为,矩形的宽为,由此得到
,即为,
6.C
【详解】
解:由图2可知,当P点位于B点时,,即,
当P点位于E点时,,即,则,
∵,
∴,
即,
∵
∴,
∵点为的中点,
∴,
7.B
【详解】
解:∵全班有x名学生,
∴每名学生应该送的相片为(x-1)张,
∴x(x-1)=2550.
故选:B.
9.B
【详解】
解:通过观察图形可知:
第一行有1个点,第二行有2个点…第n行有n个点,
则前5行共有(1+2+3+4+5)个点,
前10行共有(1+2+3+4+5+6+7+8+9+10)个点,
前n行共有1+2+3+4+5+…+n=n(n+1)个点,
其中n为正整数,
∴当n(n+1)=741时,解得:(舍),,
当n(n+1)=600时,解得: (舍),
当n(n+1)=465时,解得:(舍),,
当n(n+1)=300时,解得:(舍),,
10.B
【详解】
解:设矩形的长为xcm,宽为ycm,
依题意,得:,
(②-①)÷3,得:y-x+1=0,
∴x=y+1③.
将③代入②,得:y(y+1)=16+3(y-4)+11,
整理,得:y2-2y-15=0,
解得:y1=5,y2=-3(舍去),
∴x=6.
∴按图③放置时,矩形纸片没有被两个正方形纸片覆盖的部分的面积为:(x-4)(y-3)+
(x-3)(y-4)=2×2+3×1=7.
11.B
【分析】
设应降价x元,根据题意列写方程并求解可得答案.
【详解】
设应降价x元
则根据题意,等量方程为:(65-x-45)(30+5x)=800
解得:x=4或x=10
∵要尽快较少库存,∴x=4舍去
故选:B.
12.A
【详解】
解:∵四边形ABCD为正方形
∴∠BAD=∠B=∠D=90°,AB=AD=BC=CD
∵△AEF为等边三角形
∴AE=AF,∠EAF=60°
在Rt△ABE和Rt△ADF中
∴Rt△ABE≌Rt△ADF
∴BE=DF,∠BAE=∠DAF
∴BC-BE=CD-DF
∴CE=CF,故①正确;
∴∠BAE=∠DAF=(∠BAC-∠EAF)=15°
∴∠AEB=90°-∠BAE=75°,故②正确;
在Rt△ABE中,∠BAE≠30°
∴AE≠2BE
∴EF≠BE+DF,故③错误;
设正方形的边长为x,
∵CE=CF,∠C=90°,EF=2
∴△CEF为等腰直角三角形
∴∠CEF=45°
∴CE=
则BE=BC-CE=x-
在Rt△ABE中,AB2+BE2=AE2
∴x2+(x-)2=22
解得:x1=,x2=(不符合实际,舍去)
∴=,故④正确.
综上:正确的有①②④.
13.24
【详解】
设每轮传染中平均一人传染人,则第一轮有人感染,第二轮有人感染,根据题意可得:
解得:(不符题意,舍去)
故答案为24
14.50.7(1+x)2=125.6
【详解】
解:依题意,得:50.7(1+x)2=125.6.
故答案为:50.7(1+x)2=125.6.
15.
【详解】
解:设平均每年增产的百分率为x;
第一年粮食的产量为:300(1+x);
第二年粮食的产量为:300(1+x)(1+x)=300(1+x)2;
依题意,可列方程:300(1+x)2=363;
故答案为:300(1+x)2=363.
16.
【详解】
设经过秒后,P,Q两点间距离为厘米,
由题意得:点P从点A开始沿AB边运动到点B所需时间为秒,
点Q从点B开始沿BC边运动到点C所需时间为秒,
因此,分以下三种情况:
(1)当点Q到达点C之前,即时,则厘米,厘米,
厘米,
厘米,
则在中,,即,
整理得:,
解得或(不符题设,舍去);
(2)当点Q到达点C,点P继续向点B移动,即时,则厘米,
由得:,
整理得:,
解得或(均不符题设,舍去);
(3)当点Q到达点C,点P到达点B,即时,
则厘米,不符题意;
综上,经过秒后,P,Q两点间距离为厘米,
故答案为:.
17.6
【详解】
观察题图得第1个图形有(个)小圆圈,
第2个图形有(个)小圆圈,
第3个图形有(个)小圆圈,…,
第n个图形有个小圆圈.
令,
解得,(舍去).
18.
【详解】
解:过作于,过作交的延长线于,
,,
,
,
在与中,
,
,
,,
,
,
设,,
在中,,即:,
解得:;(不合题意,舍去).
,,
,
.
19.(1)养鸡场的宽是10m,长为15m;(2)围成养鸡场的面积不能达到200m2,见解析
【分析】
(1)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,求出x的值即可,注意x要符合题意;
(2)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,判断出△的值,即可得出答案.
【详解】
解:(1)设养鸡场的宽为xm,根据题意得:
x(35﹣2x)=150,
解得:x1=10,x2=7.5,
当x1=10时,35﹣2x=15<18,
当x2=7.5时35﹣2x=20>18,(舍去),
则养鸡场的宽是10m,长为15m.
(2)设养鸡场的宽为xm,根据题意得:
x(35﹣2x)=200,
整理得:2x2﹣35x+200=0,
△=(﹣35)2﹣4×2×200=1225﹣1600=﹣375<0,
因为方程没有实数根,
所以围成养鸡场的面积不能达到200m2.
20.(1)售价32元/件,进价24元/件;(2)3元
【分析】
(1)根据题目,设出未知数,列出一元一次方程即可求解;
(2)根据题目:利润=每件利润×销售数量,列出一元二次方程求解即可.
【详解】
解:(1)设商品的进价为每件元,则售价为每件元,
由题意可得:,
解得,
∴,
答:商品的售价和进价分别是32元/件、24元/件;
(2)设该商品应再涨价元,
由题意可得:,
解得:或,
∵每天所得的销售利润为2035元时,且销售量尽可能大,
∴,
答:该商品应再涨价3元.
21.(1)-2,1;(2)x=3;(3)4
【分析】
(1)利用因式分解法解方程;
(2)把无理方程化为整式方程x2﹣2x﹣3=0,然后利用因式分解法解方程后进行检验确定原方程的解;
(3)先表示得到(x+)2﹣3(x+)﹣4=0,利用因式分解法得到x+=4或x+=﹣1,由于x+=﹣1化为x2+x+1=0,此方程没有实数解,从而得到x+的值为4.
【详解】
解:(1)x3+x2﹣2x=0,
x(x2+x﹣2)=0,
x(x+2)(x﹣1)=0,
x=0或x+2=0或x﹣1=0,
所以x1=0,x2=﹣2,x3=1;
故答案为0,﹣2,1;
(2)两边平方得2x+3=x2,
整理得x2﹣2x﹣3=0,
因式分解得
解得x1=3,x2=﹣1,
经检验,x=3为原方程的解;
(3)=2,
,
,
或,
∵化为x2+x+1=0,△=1-4=-4,此方程没有实数解舍去,
∴x+的值为4.
22.(1)10%;(2)13.31万
【分析】
(1)设这两个月参观人数的月平均增长率为,根据题意列出等式解出即可;
(2)直接利用(1)中求出的月平均增长率计算即可.
【详解】
(1)解:设这两个月参观人数的月平均增长率为,
由题意得:,
解得:,(不合题意,舍去),
答:这两个月参观人数的月平均增长率为.
(2)(万人),
答:六月份的参观人数为13.31万人.
23.(1)t1=2,t2=4;(2)t的值为或2时,重叠面积为8.
【分析】
(1)先求出△ABC的面积,然后根据题意可得AP=t,CP=6﹣t,然后再△PBC与△PAD的面积和是△ABC的面积的,列出方程、解方程即可解答;
(2)根据不同时间段分三种情况进行解答即可.
【详解】
(1)∵Rt△ABC中,∠ACB=90°,AC=BC=6,
∴S△ABC=×6×6=18,
∵AP=t,CP=6﹣t,
∴△PBC与△PAD的面积和=t2+×6×(6﹣t),
∵△PBC与△PAD的面积和是△ABC的面积的,
∴t2+×6×(6﹣t)=18×,
解之,得t1=2,t2=4;
(2)∵AP=t,PQ=2AP,
∴PQ=2t,
①如图1,当0≤t≤2时,S=(2t)2﹣t2=t2=8,
解得:t1=,t2=﹣(不合题意,舍去),
②如图2,当2≤t≤3时,S=×6×6﹣t2﹣(6﹣2t)2=12t﹣t2=8,
解得:t1=4(不合题意,舍去),t2=(不合题意,舍去),
③如图3,当3≤t≤6时,S= 6×6﹣t2=8,
解得:t1=2,t 2=﹣2(不合题意,舍去),
综上,t的值为或2时,重叠面积为8.
_21?????????è?????(www.21cnjy.com)_
人教版2021年九年级上册数学同步练习卷
21.3 实际问题与一元二次方程
一、单选题
1.主题为“绿色城市、健康生活”的世界园艺博览会将于2021年4月至10月在枣林湾举行.世园会的某纪念品受到热烈欢迎,从原价50元连续两次涨价达到72元,如果每次涨价的百分率都是x,则下面所列方程正确的是( )
A. B.
C. D.
2.如图,把一块长为50cm,宽为40cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为400cm2,设剪去小正方形的边长为xcm,则可列方程为( )
A. B.
C. D.
3.某商品连续两次降价,每件零售价由原来的56元降到了31.5元,若设平均每次降价的百分率为,则可列方程为( )
A. B.
C. D.
4.若比与的积小1,则关于的值,下列说法正确的是( )
A.不存在这样的值 B.有两个相等的的值
C.有两个不相等的的值 D.无法确定
5.用总长的铝合金材料做一个如图所示的窗框(不计损耗),窗框的上部是等腰直角三角形,下部是一个矩形,窗框的总面积为(材料的厚度忽略不计).若设等腰直角三角形的斜边长为,则下列方程符合题意的是( ).
A. B.
C. D.
6.如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
A. B. C. D.
7.某班学生毕业时,每一位同学都向全班其他同学送一张自己的相片作为纪念,全班共送了2550张相片,若设全班有名学生,则可列方程为( )
A. B.
C. D.
8.如图①,在矩形中,,对角线,相交于点,动点由点出发,沿向点运动.设点的运动路程为,的面积为,与的函数关系图象如图②所示,则对角线的长为( )
A.3 B.4 C.5 D.6
9.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第行有个点…,前行的点数和不能是以下哪个结果 ( )
A.741 B.600 C.465 D.300
10.一个矩形内放入两个边长分别为3cm和4cm的小正方形纸片,按照图①放置,矩形纸片没有被两个正方形纸片覆盖的部分(黑色阴影部分)的面积为8cm2;按照图②放置,矩形纸片没有被两个正方形纸片覆盖的部分的面积为11cm2,若把两张正方形纸片按图③放置时,矩形纸片没有被两个正方形纸片覆盖的部分的面积为( )
A.6cm2 B.7 cm2 C.12cm2 D.19 cm2
11.某商场将进货价为45元的某种服装以65元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价( )
A.12元 B.10元 C.11元 D.9元
12.如图,在正方形中,边长为的等边三角形的顶点分别在和上,下列结论:,其中正确的序号是( )
A.①②④ B.①② C.②③④ D.①③④
二、填空题
13.有一人感染了传染性很强的病毒,经过两轮传染后共有625人患病,每轮传染中平均一人传染______人.
14.新能源汽车节能环保,越来越受到消费者的喜爱,各种品牌相继投放市场.某地2018年新能源汽车的销售量为50.7万辆,销售量逐年增加,到2020年为125.6万辆.若年增长率x不变,则x的值是多少?根据题意可列方程为_________.
15.劳动教育己纳入人才培养全过程,某学校加大投入,建设校园农场,该农场一种作物的产量两年内从300千克增加到363千克.设平均每年增产的百分率为,则可列方程为________.
16.在中,,厘米,厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过______秒后,P,Q两点间距离为厘米.
17.观察下列图形,第1个图形中一共有4个小圆圈,第2个图形中一共有10个小圆圈,第3个图形中一共有18个小圆圈,…,第_____个图形中一共有54个小圆圈……按此规律排列,则第n个图形中小圆圈的个数是___________.
18.已知:如图,等腰直角,,,点D为外一点,,连接CD,,,BC的长为________.
三、解答题
19.如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.
(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由.
20.突如其来的新冠疫情影响了某商场的经济效益,在复工复产后商场对某种商品价格进行了调整,将该种商品的进价提高了8元定为销售价格,此时该商品8件的进价恰好相当于6件的售价,且每天可售出200件.经市场调查发现:如果该商品每件再涨价1元,每天就会少售出5件.
(1)该商品的售价和进价各是多少元?
(2)若在进价不变的条件下,确保每天所得的销售利润为2035元,且销售量尽可能大,则该商品应再涨价多少元?
21.苏科版九上数学p31阅读《各类方程的解法》中提到:各类方程的解法不尽相同,但是它们有一个共同的基本数学思想﹣﹣转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= ;
(2)用“转化”思想求方程=x的解;
(3)拓展:若实数x满足x2+=2,求x+的值
22.2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
23.Rt△ABC中,∠ACB=90°,AC=BC=6,动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动,到达点C停止运动.设运动时间为t秒
(1)如图1,过点P作PD⊥AC,交AB于D,若△PBC与△PAD的面积和是△ABC的面积的,求t的值;
(2)点Q在射线PC上,且PQ=2AP,以线段PQ为边向上作正方形PQNM.在运动过程中,若设正方形PQNM与△ABC重叠部分的面积为8,求t的值.
参考答案
1.D
【详解】
解:每次涨价的百分率都是,则第一次涨价后价格为元,第二次涨价后价格为
所以
2.B
【详解】
根据题意,底面矩形的长为:,宽为:,根据题意得:
3.A
【详解】
设平均每次降价的百分率为
第一次降价后的价格为:
第二次降价后的价格为:
∴可列方程
4.C
【详解】
解:由题意,得,
整理得,
∵,
∴方程有两个不相等的实数根,
即,,
5.D
【详解】
解:设等腰直角三角形的斜边长为,则等腰直角三角形的直角边长为,矩形的宽为,由此得到
,即为,
6.C
【详解】
解:由图2可知,当P点位于B点时,,即,
当P点位于E点时,,即,则,
∵,
∴,
即,
∵
∴,
∵点为的中点,
∴,
7.B
【详解】
解:∵全班有x名学生,
∴每名学生应该送的相片为(x-1)张,
∴x(x-1)=2550.
故选:B.
9.B
【详解】
解:通过观察图形可知:
第一行有1个点,第二行有2个点…第n行有n个点,
则前5行共有(1+2+3+4+5)个点,
前10行共有(1+2+3+4+5+6+7+8+9+10)个点,
前n行共有1+2+3+4+5+…+n=n(n+1)个点,
其中n为正整数,
∴当n(n+1)=741时,解得:(舍),,
当n(n+1)=600时,解得: (舍),
当n(n+1)=465时,解得:(舍),,
当n(n+1)=300时,解得:(舍),,
10.B
【详解】
解:设矩形的长为xcm,宽为ycm,
依题意,得:,
(②-①)÷3,得:y-x+1=0,
∴x=y+1③.
将③代入②,得:y(y+1)=16+3(y-4)+11,
整理,得:y2-2y-15=0,
解得:y1=5,y2=-3(舍去),
∴x=6.
∴按图③放置时,矩形纸片没有被两个正方形纸片覆盖的部分的面积为:(x-4)(y-3)+
(x-3)(y-4)=2×2+3×1=7.
11.B
【分析】
设应降价x元,根据题意列写方程并求解可得答案.
【详解】
设应降价x元
则根据题意,等量方程为:(65-x-45)(30+5x)=800
解得:x=4或x=10
∵要尽快较少库存,∴x=4舍去
故选:B.
12.A
【详解】
解:∵四边形ABCD为正方形
∴∠BAD=∠B=∠D=90°,AB=AD=BC=CD
∵△AEF为等边三角形
∴AE=AF,∠EAF=60°
在Rt△ABE和Rt△ADF中
∴Rt△ABE≌Rt△ADF
∴BE=DF,∠BAE=∠DAF
∴BC-BE=CD-DF
∴CE=CF,故①正确;
∴∠BAE=∠DAF=(∠BAC-∠EAF)=15°
∴∠AEB=90°-∠BAE=75°,故②正确;
在Rt△ABE中,∠BAE≠30°
∴AE≠2BE
∴EF≠BE+DF,故③错误;
设正方形的边长为x,
∵CE=CF,∠C=90°,EF=2
∴△CEF为等腰直角三角形
∴∠CEF=45°
∴CE=
则BE=BC-CE=x-
在Rt△ABE中,AB2+BE2=AE2
∴x2+(x-)2=22
解得:x1=,x2=(不符合实际,舍去)
∴=,故④正确.
综上:正确的有①②④.
13.24
【详解】
设每轮传染中平均一人传染人,则第一轮有人感染,第二轮有人感染,根据题意可得:
解得:(不符题意,舍去)
故答案为24
14.50.7(1+x)2=125.6
【详解】
解:依题意,得:50.7(1+x)2=125.6.
故答案为:50.7(1+x)2=125.6.
15.
【详解】
解:设平均每年增产的百分率为x;
第一年粮食的产量为:300(1+x);
第二年粮食的产量为:300(1+x)(1+x)=300(1+x)2;
依题意,可列方程:300(1+x)2=363;
故答案为:300(1+x)2=363.
16.
【详解】
设经过秒后,P,Q两点间距离为厘米,
由题意得:点P从点A开始沿AB边运动到点B所需时间为秒,
点Q从点B开始沿BC边运动到点C所需时间为秒,
因此,分以下三种情况:
(1)当点Q到达点C之前,即时,则厘米,厘米,
厘米,
厘米,
则在中,,即,
整理得:,
解得或(不符题设,舍去);
(2)当点Q到达点C,点P继续向点B移动,即时,则厘米,
由得:,
整理得:,
解得或(均不符题设,舍去);
(3)当点Q到达点C,点P到达点B,即时,
则厘米,不符题意;
综上,经过秒后,P,Q两点间距离为厘米,
故答案为:.
17.6
【详解】
观察题图得第1个图形有(个)小圆圈,
第2个图形有(个)小圆圈,
第3个图形有(个)小圆圈,…,
第n个图形有个小圆圈.
令,
解得,(舍去).
18.
【详解】
解:过作于,过作交的延长线于,
,,
,
,
在与中,
,
,
,,
,
,
设,,
在中,,即:,
解得:;(不合题意,舍去).
,,
,
.
19.(1)养鸡场的宽是10m,长为15m;(2)围成养鸡场的面积不能达到200m2,见解析
【分析】
(1)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,求出x的值即可,注意x要符合题意;
(2)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,判断出△的值,即可得出答案.
【详解】
解:(1)设养鸡场的宽为xm,根据题意得:
x(35﹣2x)=150,
解得:x1=10,x2=7.5,
当x1=10时,35﹣2x=15<18,
当x2=7.5时35﹣2x=20>18,(舍去),
则养鸡场的宽是10m,长为15m.
(2)设养鸡场的宽为xm,根据题意得:
x(35﹣2x)=200,
整理得:2x2﹣35x+200=0,
△=(﹣35)2﹣4×2×200=1225﹣1600=﹣375<0,
因为方程没有实数根,
所以围成养鸡场的面积不能达到200m2.
20.(1)售价32元/件,进价24元/件;(2)3元
【分析】
(1)根据题目,设出未知数,列出一元一次方程即可求解;
(2)根据题目:利润=每件利润×销售数量,列出一元二次方程求解即可.
【详解】
解:(1)设商品的进价为每件元,则售价为每件元,
由题意可得:,
解得,
∴,
答:商品的售价和进价分别是32元/件、24元/件;
(2)设该商品应再涨价元,
由题意可得:,
解得:或,
∵每天所得的销售利润为2035元时,且销售量尽可能大,
∴,
答:该商品应再涨价3元.
21.(1)-2,1;(2)x=3;(3)4
【分析】
(1)利用因式分解法解方程;
(2)把无理方程化为整式方程x2﹣2x﹣3=0,然后利用因式分解法解方程后进行检验确定原方程的解;
(3)先表示得到(x+)2﹣3(x+)﹣4=0,利用因式分解法得到x+=4或x+=﹣1,由于x+=﹣1化为x2+x+1=0,此方程没有实数解,从而得到x+的值为4.
【详解】
解:(1)x3+x2﹣2x=0,
x(x2+x﹣2)=0,
x(x+2)(x﹣1)=0,
x=0或x+2=0或x﹣1=0,
所以x1=0,x2=﹣2,x3=1;
故答案为0,﹣2,1;
(2)两边平方得2x+3=x2,
整理得x2﹣2x﹣3=0,
因式分解得
解得x1=3,x2=﹣1,
经检验,x=3为原方程的解;
(3)=2,
,
,
或,
∵化为x2+x+1=0,△=1-4=-4,此方程没有实数解舍去,
∴x+的值为4.
22.(1)10%;(2)13.31万
【分析】
(1)设这两个月参观人数的月平均增长率为,根据题意列出等式解出即可;
(2)直接利用(1)中求出的月平均增长率计算即可.
【详解】
(1)解:设这两个月参观人数的月平均增长率为,
由题意得:,
解得:,(不合题意,舍去),
答:这两个月参观人数的月平均增长率为.
(2)(万人),
答:六月份的参观人数为13.31万人.
23.(1)t1=2,t2=4;(2)t的值为或2时,重叠面积为8.
【分析】
(1)先求出△ABC的面积,然后根据题意可得AP=t,CP=6﹣t,然后再△PBC与△PAD的面积和是△ABC的面积的,列出方程、解方程即可解答;
(2)根据不同时间段分三种情况进行解答即可.
【详解】
(1)∵Rt△ABC中,∠ACB=90°,AC=BC=6,
∴S△ABC=×6×6=18,
∵AP=t,CP=6﹣t,
∴△PBC与△PAD的面积和=t2+×6×(6﹣t),
∵△PBC与△PAD的面积和是△ABC的面积的,
∴t2+×6×(6﹣t)=18×,
解之,得t1=2,t2=4;
(2)∵AP=t,PQ=2AP,
∴PQ=2t,
①如图1,当0≤t≤2时,S=(2t)2﹣t2=t2=8,
解得:t1=,t2=﹣(不合题意,舍去),
②如图2,当2≤t≤3时,S=×6×6﹣t2﹣(6﹣2t)2=12t﹣t2=8,
解得:t1=4(不合题意,舍去),t2=(不合题意,舍去),
③如图3,当3≤t≤6时,S= 6×6﹣t2=8,
解得:t1=2,t 2=﹣2(不合题意,舍去),
综上,t的值为或2时,重叠面积为8.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
