22.1.1 二次函数 课时达标检测(含解析)
文档属性
| 名称 | 22.1.1 二次函数 课时达标检测(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年九年级上册数学同步练习卷
22.1二次函数的图像和性质
22.1.1 二次函数
一、单选题
1.下列各式中,是的二次函数的是( )
A. B. C. D.
2.下列函数:(1)y=3x2﹣+1;(2)y=;(3)y=1﹣x2;(4)y=ax2+bx+c;(5)y=+x;(6)y=x2﹣(x﹣1)x.属于二次函数的有( )
A.1个 B.2个 C.3个 D.4个
3.一个边长为2厘米的正方形,如果它的边长增加厘米,则面积随之增加平方厘米,那么与之间满足的函数关系是( )
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
4.若函数是二次函数,那么的值是( )
A.2 B.-2或2 C.-2 D.0或2
5.若函数y=(a﹣1)x2+2x+a2﹣1是二次函数,则( )
A.a≠1 B.a≠﹣1 C.a=1 D.a=±1
6.已知函数:①y=2x﹣1;②y=﹣2x2﹣1;③y=3x3﹣2x2;④y=2(x+3)2-2x2;⑤y=ax2+bx+c,其中二次函数的个数为( )
A.1 B.2 C.3 D.4
7.关于二次函数,以下结论:①抛物线交轴有两个不同的交点;②不论取何值,抛物线总是经过一个定点;③设抛物线交轴于、两点,若,则;④抛物线的顶点在图象上;⑤抛物线交轴于点,若是等腰三角形,则,,.其中正确的序号是( )
A.①②⑤ B.②③④ C.①④⑤ D.②④
8.已知函数y=(m2+m)+mx+4为二次函数,则m的取值范围是( )
A.m≠0 B.m ≠-1 C.m≠0,且m≠-1 D.m=-1
9.下列函数关系中,可以看作二次函数()模型的是( )
A.在一定的距离内汽车的行驶速度与行驶时间的关系
B.我国人口年自然增长率为1%,这样我国人口总数随年份的变化关系
C.竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D.圆的周长与圆的半径之间的关系
10.设y=y1﹣y2,y1与x成正比例,y2与x2成正比例,则y与x的函数关系是( )
A.正比例函数 B.一次函数
C.二次函数 D.以上均不正确
11.已知函数y=ax2+bx+c,其中a,b,c可在0,1,2,3,4五个数中取值,则不同的二次函数的个数共有( )
A.125个 B.100个 C.48个 D.10个
12.如果函数是二次函数,则的取值范围是( )
A. B. C.=﹣2 D.为全体实数
二、填空题
13.已知函数是二次函数,则的取值范围是__________.
14.二次函数的图象经过原点,则__________.
15.如图,正方形的边长为2,与负半轴的夹角为15°,点在抛物线的图象上,则的值为_.
16.某二次函数的图像的顶点坐标(4,-1),且它的形状、开口方向与抛物线y=-x2相同,则这个二次函数的解析式为________
17.抛物线经过点,当时,当时,则的取值范围是__________.
18.开口向下的抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),则m=_____.
三、解答题
19.已知抛物线y=﹣x2+bx+c经过点A (3,0),B (﹣1,0),求抛物线的解析式.
已知是关于的二次函数,试确定的值
21.抛物线y=mx2﹣4m(m>0)与x轴交于A,B两点(A点在B点左边),与y轴交于C点,已知OC=2OA.求:
(1)A,B两点的坐标;
(2)抛物线的解析式.
22.已知:抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,直线y=﹣x+3经过B、C两点
(1)填空:b= (用含有a的代数式表示);
(2)若a=﹣1
①点P为抛物线上一动点,过点P作PM∥y轴交直线y=﹣x+3于点M,当点P在第一象限内时,是否存在一点P,使△PCB面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
②当m≤x≤m+3时,y的取值范围是2m≤y≤4,求m的值.
23.某种型号的电热水器工作过程如下:在接通电源以后,从初始温度20下加热水箱中的水,当水温达到设定温度60时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30时,再次自动加热水箱中的水至60,加热停止;当水箱中的水温下降到30时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温是时间的函数,其中(单位:)表示水箱中水的温度,(单位:)表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
(1)小宇记录了从初始温度20第一次加热至设定温度60,之后水温冷却至保温温度30的过程中,随的变化情况,如下表所示:
接通电源后的时间() 0 2 4 8 10 12 14 16 18 20 …
水箱中水的温度() 20 30 40 60 51 45 40 36 33 30
①请写出一个符合加热阶段与关系的函数解析式______________;
②根据该电热水器的工作特点,当第二次加热至设定温度60时,距离接通电源的时间为________.
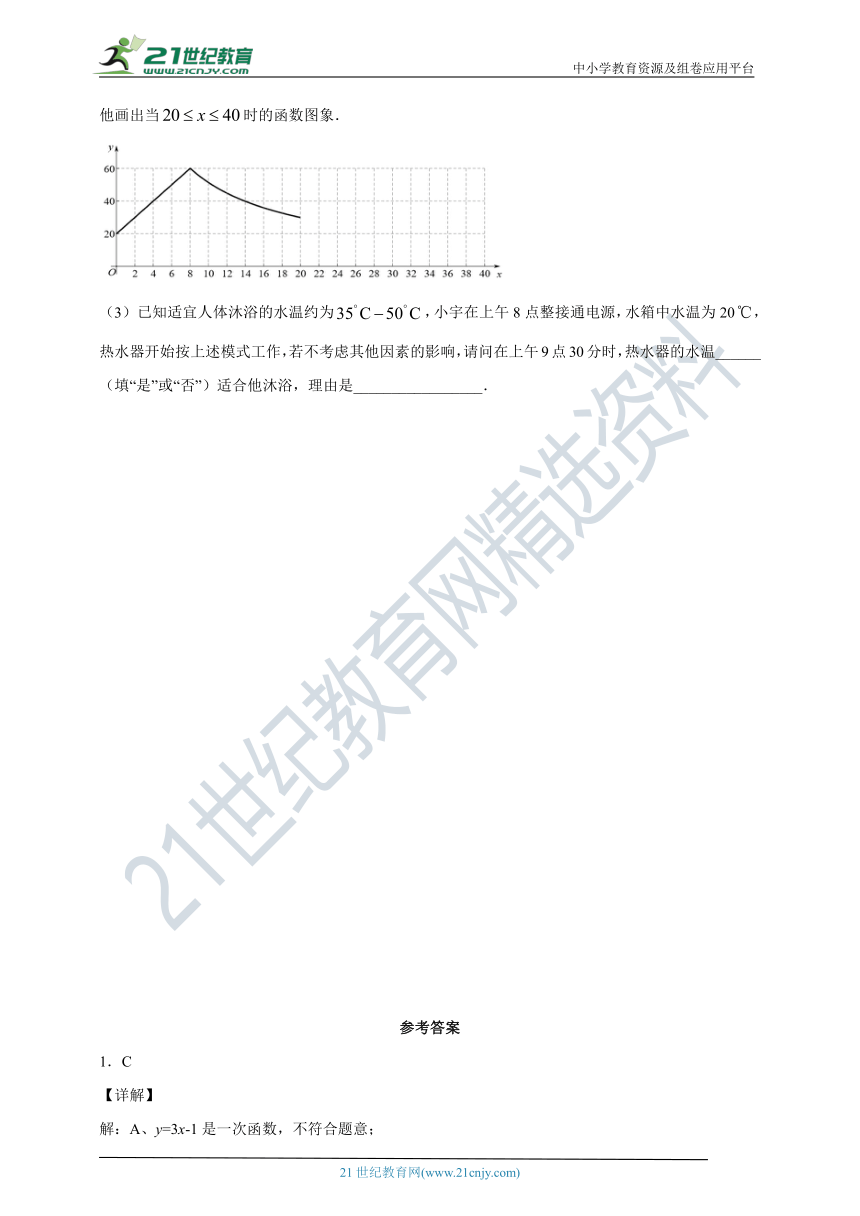
(2)根据上述的表格,小宇画出了当时的函数图象,请根据该电热水器的工作特点,帮他画出当时的函数图象.
已知适宜人体沐浴的水温约为,小宇在上午8点整接通电源,水箱中水温为20,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
参考答案
1.C
【详解】
解:A、y=3x-1是一次函数,不符合题意;
B、中右边不是整式,不是二次函数,不符合题意;
C、y=3x2+x-1是二次函数,符合题意;
D、中右边不是整式,不是二次函数,不符合题意;
2.B
【详解】
解:由题可得,属于二次函数的为:(2)y=;(3)y=1﹣x2;共2个,
3.D
【详解】
解:由题意得,
与之间满足的函数关系是二次函数,
4.A
【详解】
∵函数是二次函数,
∴且,
∴
5.A
【详解】
解:由题意得:a﹣1≠0,
解得:a≠1,
6.A
【详解】
y=2x﹣1是一次函数;
y=﹣2x2﹣1是二次函数;
y=3x3﹣2x2不是二次函数;
④y=2(x+3)2-2x2,不是二次函数;
y=ax2+bx+c,没告诉a不为0,故不是二次函数;
故二次函数有1个;
7.D
【解析】
令,利用该一元二次方程的△即可判断①的正误;当x=1时,方程中变化的参数k会被“抵消”,则抛物线总是会经过一个定点,由此判断②;可直接代入k=4来验证③;求出顶点坐标,然后代入,来判断④;可采取直接代入进行验证,选择较容易的0和1先代入,当k=1时,不是等腰三角形.
【详解】
解:△=k2-4k+4=(k-2)2≥0,当k=2时,抛物线与x轴只有1个交点,①错误;
当x=1时,y=1-k+k-1=0,即抛物线过定点(1,0),②正确;
当k=4时,y=x2-4x+3,则抛物线与x轴的交点为:x2-4x+3=0,解得x1=3,x2=1,则AB=3-1=2,故③错误;
二次函数的顶点为(,),代入进行验证:
当x=时,,故④正确;
当k=1时,,解得抛物线与x轴的两个交点为:(0,0)、(1,0),此时不是等腰三角形,故⑤错误.
8.C
【详解】
由y=(m2+m)+mx+4为二次函数,得m2+m≠0,解得m≠0,m≠-1,
9.C
【详解】
A、v=,是反比例函数,错误;B、y=m(1+1%)x,不是二次函数,错误;C、S=-x2+cx,是二次函数,正确;D、C=2πr,是正比例函数,错误,
10.C
【详解】
解:设y1=k1x,y2=k2x2,
则y=k1x﹣k2x2,
所以y是关于x的二次函数,
11.B
【详解】
由题意,
∴a有四种选法:1、2、3、4,
∵b和c都有五种选法:0、1、2、3、4,
∴共有=100种,
12.C
【详解】
解:由题意得:m-2≠0,,
解得:m=-2,
13.
【详解】
解:∵函数是二次函数
∴,解得:
故答案为:
14.3
【详解】
解:根据二次函数图象过原点,把代入解析式,
得,整理得,解得,
∵,
∴,
∴.
故答案为:3.
15.
【详解】
如图,连接OB,过点B作BD⊥x轴于D,
∵四边形OABC是边长为2的正方形,
∴∠BOA=45°,OB=,
∵AC与x轴负半轴的夹角为15°,
∴∠AOD=45°﹣15°=30°,
∴BD= OB= ,OD= = = ,
∴点B的坐标为(,),
∵点B在抛物线的图象上,
则:,
解得:,
故答案为
故答案为:.
16.y=-(x-4)2-1
【详解】
试题分析:根据题意,可由二次函数的形状、开口方向与抛物线y=-x2相同,设函数的解析式为y=-(x-a)2+h,可直接代入得到y=-(x-4)2-1.
故答案为:y=-(x-4)2-1.
17.
【分析】
将点代入,得,再将x与y的对应关系代入函数解析式得到不等式组,解不等式组即可求得k的取值范围.
【详解】
将点代入,
得36a+k=2,
∴,
当时,当时得,
解得,
∴,
故填.
18.-1
【详解】
由于抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),
∴对称轴为直线x=-1,x==-1,
解得m1=-1,m2=2.
由于抛物线的开口向下,所以当m=2时,m2-2=2>0,不合题意,应舍去,
∴m=-1.
故答案为-1.
19.y=﹣x2+2x+3
【分析】
直接利用交点式写出抛物线解析式.
【详解】
解:抛物线的解析式为y=﹣(x﹣3)(x+1),
即y=﹣x2+2x+3.
20.
【详解】
解:根据题意得,,解得,,
∵,即,
∴.
21.(1)A(﹣2,0),B(2,0);(2)y=x2﹣4
【分析】
(1)通过解方程mx?﹣4m=0可得A、B点的坐标;
(2)先利用OA=2得到OC=4,所以|﹣4m|=4,然后求出满足条件的m的值,从而得到抛物线解析式.
【详解】
解:(1)当y=0时,mx2﹣4m=0,即x2﹣4=0,解得x1=2,x2=﹣2,
∴A(﹣2,0),B(2,0);
(2)当x=0时,y=mx2﹣4m=﹣4m,
∴C(0,﹣4m),
∵OA=2,
∴OC=2OA=4,
∴|﹣4m|=4,解得m=1或m=﹣1,
∵m>0,
∴m=1,
∴抛物线解析式为y=x2﹣4.
22.(1)﹣3a﹣1;(2)①P( ,);②m的值为0或﹣.
【分析】
(1)直线经过B、C两点,先求出两点坐标,再带入抛物线解析式中求出表达式,然后再得到结果(2)若a=-1时,先写出抛物线解析式,然后根据条件求点P的坐标,再根据已知的m的范围,对照函数图象,求出m的值.
【详解】
解:(1)直线y=﹣x+3,当y=0时,x=3;当x=0时,y=3,
∴B(3,0)、C(0,3),
∵抛物线过B(3,0)、C(0,3),
∴解得:b=﹣3a﹣1,
故答案为﹣3a﹣1.
(2)若a=﹣1,则抛物线的解析式为y=﹣x2+2x+3;
①假设存在点P(x,﹣x2+2x+3)使得△PCB的面积最大,
∴M(x,﹣x+3),
∴PM=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,
∵S△ABP=S△PMC+S△PMB=PM?OB=(﹣x2+3x)×3=﹣(x2﹣3x)
=﹣(x﹣)2+,
当点P(,)在第一象限,此时△PBC的面积最大,
故存在点P的坐标为:P( ,),△PBC的面积最大.
②∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的开口向下,对称轴为直线x=1,有最大值4,
∴由题意可知m≤1,m+3≥1
当m=﹣是x=m和m+3对应的函数值相等,
当﹣<m<1时,2m=﹣(m+3)2+2(m+3)+3,
解得m1=0,m2=﹣6(不合题意舍去),
当﹣2<m<﹣时,﹣m2+2m+3=2m,
∴m=(舍)或m=﹣
故m的值为0或﹣.
23.(1)①;②;(2)见详解;(3)否;加热至9点30分的温度为,不在人体适合的温度范围内.
【分析】
(1)①根据表格数据特点,应用待定系数法求解即可;②根据表格数据先确定从加热至需要的时间,再将所得时间加上第一次加热至保温的时间即得;
(2)根据加热温度变化规律可知从加热至需要,即可确定点,
(3)根据表格数据特点,第一次加热需要20分钟,之后每18分钟一次循环,即可确定早上9点30分对应第一次加热的时间段.
【详解】
(1)①当时,设解析式为:
将代入并联立得:
,解得:
∴当时,
当时,设解析式为:
将 代入并联立得:
解得:
∴当时,
∴第一次加热阶段与关系的函数解析式为:
故答案为:
②根据表格数据可知从加热至需要
∴当第二次加热至设定温度60时,距离接通电源的时间为
故答案为:.
(2)如下图:
(3)从早上8点至早上9点30分,总共用时90分钟,且第一次加热需要20分钟至保温温度,第一次以后每18分钟循环一次.
∵,即最后一次重新加热至9点30分对应第一次的第18分钟的温度:.
∴在上午9点30分时,热水器的水温不适合他沐浴.
故答案为:否,加热至9点30分的温度为,不在人体适合的温度范围内.
_21?????????è?????(www.21cnjy.com)_
人教版2021年九年级上册数学同步练习卷
22.1二次函数的图像和性质
22.1.1 二次函数
一、单选题
1.下列各式中,是的二次函数的是( )
A. B. C. D.
2.下列函数:(1)y=3x2﹣+1;(2)y=;(3)y=1﹣x2;(4)y=ax2+bx+c;(5)y=+x;(6)y=x2﹣(x﹣1)x.属于二次函数的有( )
A.1个 B.2个 C.3个 D.4个
3.一个边长为2厘米的正方形,如果它的边长增加厘米,则面积随之增加平方厘米,那么与之间满足的函数关系是( )
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
4.若函数是二次函数,那么的值是( )
A.2 B.-2或2 C.-2 D.0或2
5.若函数y=(a﹣1)x2+2x+a2﹣1是二次函数,则( )
A.a≠1 B.a≠﹣1 C.a=1 D.a=±1
6.已知函数:①y=2x﹣1;②y=﹣2x2﹣1;③y=3x3﹣2x2;④y=2(x+3)2-2x2;⑤y=ax2+bx+c,其中二次函数的个数为( )
A.1 B.2 C.3 D.4
7.关于二次函数,以下结论:①抛物线交轴有两个不同的交点;②不论取何值,抛物线总是经过一个定点;③设抛物线交轴于、两点,若,则;④抛物线的顶点在图象上;⑤抛物线交轴于点,若是等腰三角形,则,,.其中正确的序号是( )
A.①②⑤ B.②③④ C.①④⑤ D.②④
8.已知函数y=(m2+m)+mx+4为二次函数,则m的取值范围是( )
A.m≠0 B.m ≠-1 C.m≠0,且m≠-1 D.m=-1
9.下列函数关系中,可以看作二次函数()模型的是( )
A.在一定的距离内汽车的行驶速度与行驶时间的关系
B.我国人口年自然增长率为1%,这样我国人口总数随年份的变化关系
C.竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D.圆的周长与圆的半径之间的关系
10.设y=y1﹣y2,y1与x成正比例,y2与x2成正比例,则y与x的函数关系是( )
A.正比例函数 B.一次函数
C.二次函数 D.以上均不正确
11.已知函数y=ax2+bx+c,其中a,b,c可在0,1,2,3,4五个数中取值,则不同的二次函数的个数共有( )
A.125个 B.100个 C.48个 D.10个
12.如果函数是二次函数,则的取值范围是( )
A. B. C.=﹣2 D.为全体实数
二、填空题
13.已知函数是二次函数,则的取值范围是__________.
14.二次函数的图象经过原点,则__________.
15.如图,正方形的边长为2,与负半轴的夹角为15°,点在抛物线的图象上,则的值为_.
16.某二次函数的图像的顶点坐标(4,-1),且它的形状、开口方向与抛物线y=-x2相同,则这个二次函数的解析式为________
17.抛物线经过点,当时,当时,则的取值范围是__________.
18.开口向下的抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),则m=_____.
三、解答题
19.已知抛物线y=﹣x2+bx+c经过点A (3,0),B (﹣1,0),求抛物线的解析式.
已知是关于的二次函数,试确定的值
21.抛物线y=mx2﹣4m(m>0)与x轴交于A,B两点(A点在B点左边),与y轴交于C点,已知OC=2OA.求:
(1)A,B两点的坐标;
(2)抛物线的解析式.
22.已知:抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,直线y=﹣x+3经过B、C两点
(1)填空:b= (用含有a的代数式表示);
(2)若a=﹣1
①点P为抛物线上一动点,过点P作PM∥y轴交直线y=﹣x+3于点M,当点P在第一象限内时,是否存在一点P,使△PCB面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
②当m≤x≤m+3时,y的取值范围是2m≤y≤4,求m的值.
23.某种型号的电热水器工作过程如下:在接通电源以后,从初始温度20下加热水箱中的水,当水温达到设定温度60时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30时,再次自动加热水箱中的水至60,加热停止;当水箱中的水温下降到30时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温是时间的函数,其中(单位:)表示水箱中水的温度,(单位:)表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
(1)小宇记录了从初始温度20第一次加热至设定温度60,之后水温冷却至保温温度30的过程中,随的变化情况,如下表所示:
接通电源后的时间() 0 2 4 8 10 12 14 16 18 20 …
水箱中水的温度() 20 30 40 60 51 45 40 36 33 30
①请写出一个符合加热阶段与关系的函数解析式______________;
②根据该电热水器的工作特点,当第二次加热至设定温度60时,距离接通电源的时间为________.
(2)根据上述的表格,小宇画出了当时的函数图象,请根据该电热水器的工作特点,帮他画出当时的函数图象.
已知适宜人体沐浴的水温约为,小宇在上午8点整接通电源,水箱中水温为20,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
参考答案
1.C
【详解】
解:A、y=3x-1是一次函数,不符合题意;
B、中右边不是整式,不是二次函数,不符合题意;
C、y=3x2+x-1是二次函数,符合题意;
D、中右边不是整式,不是二次函数,不符合题意;
2.B
【详解】
解:由题可得,属于二次函数的为:(2)y=;(3)y=1﹣x2;共2个,
3.D
【详解】
解:由题意得,
与之间满足的函数关系是二次函数,
4.A
【详解】
∵函数是二次函数,
∴且,
∴
5.A
【详解】
解:由题意得:a﹣1≠0,
解得:a≠1,
6.A
【详解】
y=2x﹣1是一次函数;
y=﹣2x2﹣1是二次函数;
y=3x3﹣2x2不是二次函数;
④y=2(x+3)2-2x2,不是二次函数;
y=ax2+bx+c,没告诉a不为0,故不是二次函数;
故二次函数有1个;
7.D
【解析】
令,利用该一元二次方程的△即可判断①的正误;当x=1时,方程中变化的参数k会被“抵消”,则抛物线总是会经过一个定点,由此判断②;可直接代入k=4来验证③;求出顶点坐标,然后代入,来判断④;可采取直接代入进行验证,选择较容易的0和1先代入,当k=1时,不是等腰三角形.
【详解】
解:△=k2-4k+4=(k-2)2≥0,当k=2时,抛物线与x轴只有1个交点,①错误;
当x=1时,y=1-k+k-1=0,即抛物线过定点(1,0),②正确;
当k=4时,y=x2-4x+3,则抛物线与x轴的交点为:x2-4x+3=0,解得x1=3,x2=1,则AB=3-1=2,故③错误;
二次函数的顶点为(,),代入进行验证:
当x=时,,故④正确;
当k=1时,,解得抛物线与x轴的两个交点为:(0,0)、(1,0),此时不是等腰三角形,故⑤错误.
8.C
【详解】
由y=(m2+m)+mx+4为二次函数,得m2+m≠0,解得m≠0,m≠-1,
9.C
【详解】
A、v=,是反比例函数,错误;B、y=m(1+1%)x,不是二次函数,错误;C、S=-x2+cx,是二次函数,正确;D、C=2πr,是正比例函数,错误,
10.C
【详解】
解:设y1=k1x,y2=k2x2,
则y=k1x﹣k2x2,
所以y是关于x的二次函数,
11.B
【详解】
由题意,
∴a有四种选法:1、2、3、4,
∵b和c都有五种选法:0、1、2、3、4,
∴共有=100种,
12.C
【详解】
解:由题意得:m-2≠0,,
解得:m=-2,
13.
【详解】
解:∵函数是二次函数
∴,解得:
故答案为:
14.3
【详解】
解:根据二次函数图象过原点,把代入解析式,
得,整理得,解得,
∵,
∴,
∴.
故答案为:3.
15.
【详解】
如图,连接OB,过点B作BD⊥x轴于D,
∵四边形OABC是边长为2的正方形,
∴∠BOA=45°,OB=,
∵AC与x轴负半轴的夹角为15°,
∴∠AOD=45°﹣15°=30°,
∴BD= OB= ,OD= = = ,
∴点B的坐标为(,),
∵点B在抛物线的图象上,
则:,
解得:,
故答案为
故答案为:.
16.y=-(x-4)2-1
【详解】
试题分析:根据题意,可由二次函数的形状、开口方向与抛物线y=-x2相同,设函数的解析式为y=-(x-a)2+h,可直接代入得到y=-(x-4)2-1.
故答案为:y=-(x-4)2-1.
17.
【分析】
将点代入,得,再将x与y的对应关系代入函数解析式得到不等式组,解不等式组即可求得k的取值范围.
【详解】
将点代入,
得36a+k=2,
∴,
当时,当时得,
解得,
∴,
故填.
18.-1
【详解】
由于抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),
∴对称轴为直线x=-1,x==-1,
解得m1=-1,m2=2.
由于抛物线的开口向下,所以当m=2时,m2-2=2>0,不合题意,应舍去,
∴m=-1.
故答案为-1.
19.y=﹣x2+2x+3
【分析】
直接利用交点式写出抛物线解析式.
【详解】
解:抛物线的解析式为y=﹣(x﹣3)(x+1),
即y=﹣x2+2x+3.
20.
【详解】
解:根据题意得,,解得,,
∵,即,
∴.
21.(1)A(﹣2,0),B(2,0);(2)y=x2﹣4
【分析】
(1)通过解方程mx?﹣4m=0可得A、B点的坐标;
(2)先利用OA=2得到OC=4,所以|﹣4m|=4,然后求出满足条件的m的值,从而得到抛物线解析式.
【详解】
解:(1)当y=0时,mx2﹣4m=0,即x2﹣4=0,解得x1=2,x2=﹣2,
∴A(﹣2,0),B(2,0);
(2)当x=0时,y=mx2﹣4m=﹣4m,
∴C(0,﹣4m),
∵OA=2,
∴OC=2OA=4,
∴|﹣4m|=4,解得m=1或m=﹣1,
∵m>0,
∴m=1,
∴抛物线解析式为y=x2﹣4.
22.(1)﹣3a﹣1;(2)①P( ,);②m的值为0或﹣.
【分析】
(1)直线经过B、C两点,先求出两点坐标,再带入抛物线解析式中求出表达式,然后再得到结果(2)若a=-1时,先写出抛物线解析式,然后根据条件求点P的坐标,再根据已知的m的范围,对照函数图象,求出m的值.
【详解】
解:(1)直线y=﹣x+3,当y=0时,x=3;当x=0时,y=3,
∴B(3,0)、C(0,3),
∵抛物线过B(3,0)、C(0,3),
∴解得:b=﹣3a﹣1,
故答案为﹣3a﹣1.
(2)若a=﹣1,则抛物线的解析式为y=﹣x2+2x+3;
①假设存在点P(x,﹣x2+2x+3)使得△PCB的面积最大,
∴M(x,﹣x+3),
∴PM=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,
∵S△ABP=S△PMC+S△PMB=PM?OB=(﹣x2+3x)×3=﹣(x2﹣3x)
=﹣(x﹣)2+,
当点P(,)在第一象限,此时△PBC的面积最大,
故存在点P的坐标为:P( ,),△PBC的面积最大.
②∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的开口向下,对称轴为直线x=1,有最大值4,
∴由题意可知m≤1,m+3≥1
当m=﹣是x=m和m+3对应的函数值相等,
当﹣<m<1时,2m=﹣(m+3)2+2(m+3)+3,
解得m1=0,m2=﹣6(不合题意舍去),
当﹣2<m<﹣时,﹣m2+2m+3=2m,
∴m=(舍)或m=﹣
故m的值为0或﹣.
23.(1)①;②;(2)见详解;(3)否;加热至9点30分的温度为,不在人体适合的温度范围内.
【分析】
(1)①根据表格数据特点,应用待定系数法求解即可;②根据表格数据先确定从加热至需要的时间,再将所得时间加上第一次加热至保温的时间即得;
(2)根据加热温度变化规律可知从加热至需要,即可确定点,
(3)根据表格数据特点,第一次加热需要20分钟,之后每18分钟一次循环,即可确定早上9点30分对应第一次加热的时间段.
【详解】
(1)①当时,设解析式为:
将代入并联立得:
,解得:
∴当时,
当时,设解析式为:
将 代入并联立得:
解得:
∴当时,
∴第一次加热阶段与关系的函数解析式为:
故答案为:
②根据表格数据可知从加热至需要
∴当第二次加热至设定温度60时,距离接通电源的时间为
故答案为:.
(2)如下图:
(3)从早上8点至早上9点30分,总共用时90分钟,且第一次加热需要20分钟至保温温度,第一次以后每18分钟循环一次.
∵,即最后一次重新加热至9点30分对应第一次的第18分钟的温度:.
∴在上午9点30分时,热水器的水温不适合他沐浴.
故答案为:否,加热至9点30分的温度为,不在人体适合的温度范围内.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
