22.1.3 二次函数y=a(x-h)2+k的图像和性质 课时达标检测(含解析)
文档属性
| 名称 | 22.1.3 二次函数y=a(x-h)2+k的图像和性质 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 21:52:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2021年九年级上册数学同步练习卷
22.1二次函数的图像和性质
22.1.3 二次函数y=a(x-h)2+k的图像和性质
一、单选题
1.抛物线y=5(x﹣6)2﹣2的顶点坐标是( )
A.(6,2) B.(6,﹣2) C.(﹣6,2) D.(﹣6,﹣2)
2.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
3.已知二次函数的图象经过点,,若,则的值可能是( )
A. B. C.0 D.
4.如图,在平面直角坐标系中,有一系列的抛物线(为正整数),若和的顶点的连线平行于直线,则该条抛物线对应的的值是( )
A.8 B.9 C.10 D.11
5.二次函数的图象过四个点,下列说法一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.已知点在抛物线上,则下列结论正确的是( )
A. B. C. D.
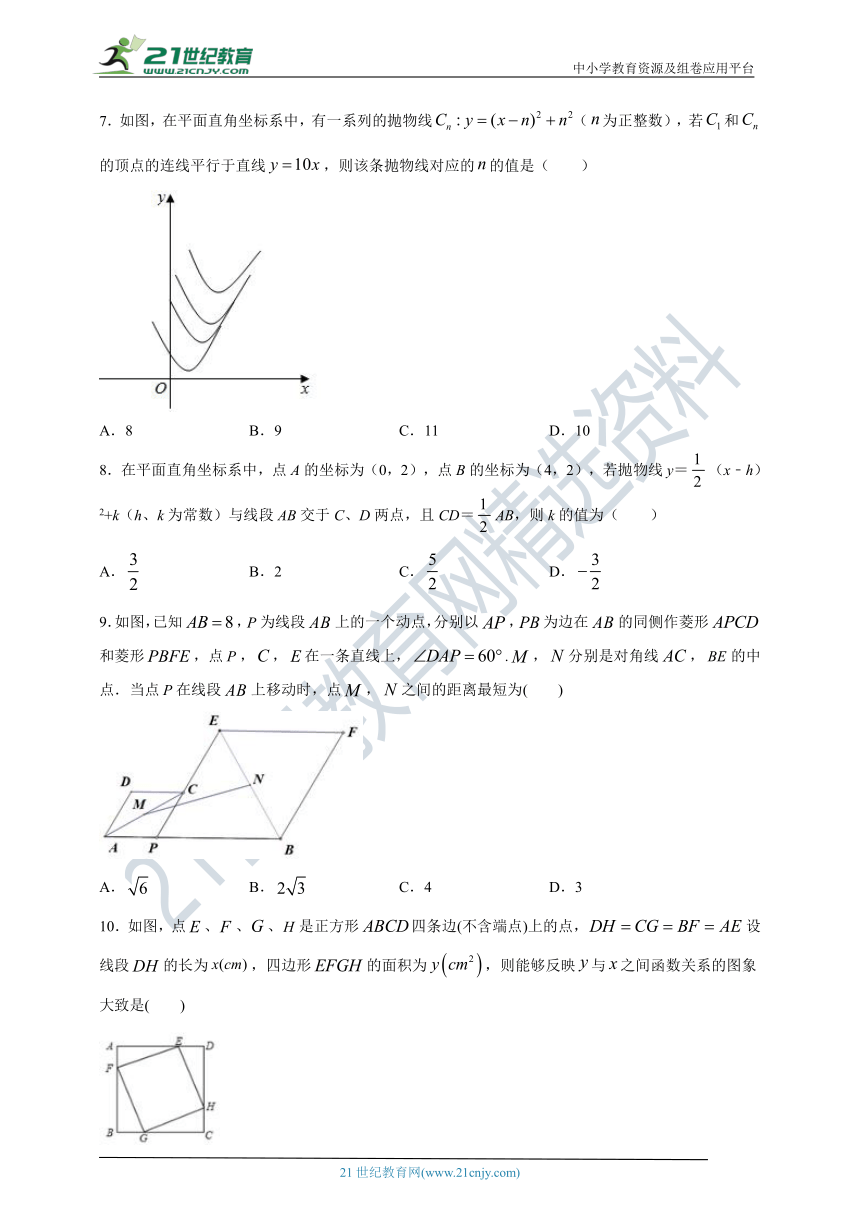
7.如图,在平面直角坐标系中,有一系列的抛物线(为正整数),若和的顶点的连线平行于直线,则该条抛物线对应的的值是( )
A.8 B.9 C.11 D.10
8.在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,2),若抛物线y=(x﹣h)2+k(h、k为常数)与线段AB交于C、D两点,且CD=AB,则k的值为( )
A. B.2 C. D.
9.如图,已知,为线段上的一个动点,分别以,为边在的同侧作菱形和菱形,点,,在一条直线上,.,分别是对角线,的中点.当点在线段上移动时,点,之间的距离最短为( )
A. B. C.4 D.3
10.如图,点、、、是正方形四条边(不含端点)上的点,设线段的长为,四边形的面积为,则能够反映与之间函数关系的图象大致是( )
A. B. C.D.
11.在同一坐标中,一次函数y=﹣kx+2与二次函数y=x2+k的图象可能是( )
A. B.
C. D.
12.如图,抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:
①a=;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
其中正确的结论是( )
A.①③④ B.①③ C.①②④ D.②
二、填空题
13.抛物线y=﹣2(x+1)2﹣3的顶点坐标是_____.
14.在抛物线图象上有三点,则的大小关系是_______
15.已知一个二次函数的图象形状与抛物线相同,且顶点坐标为,则这个二次函数的解析式为_____________.
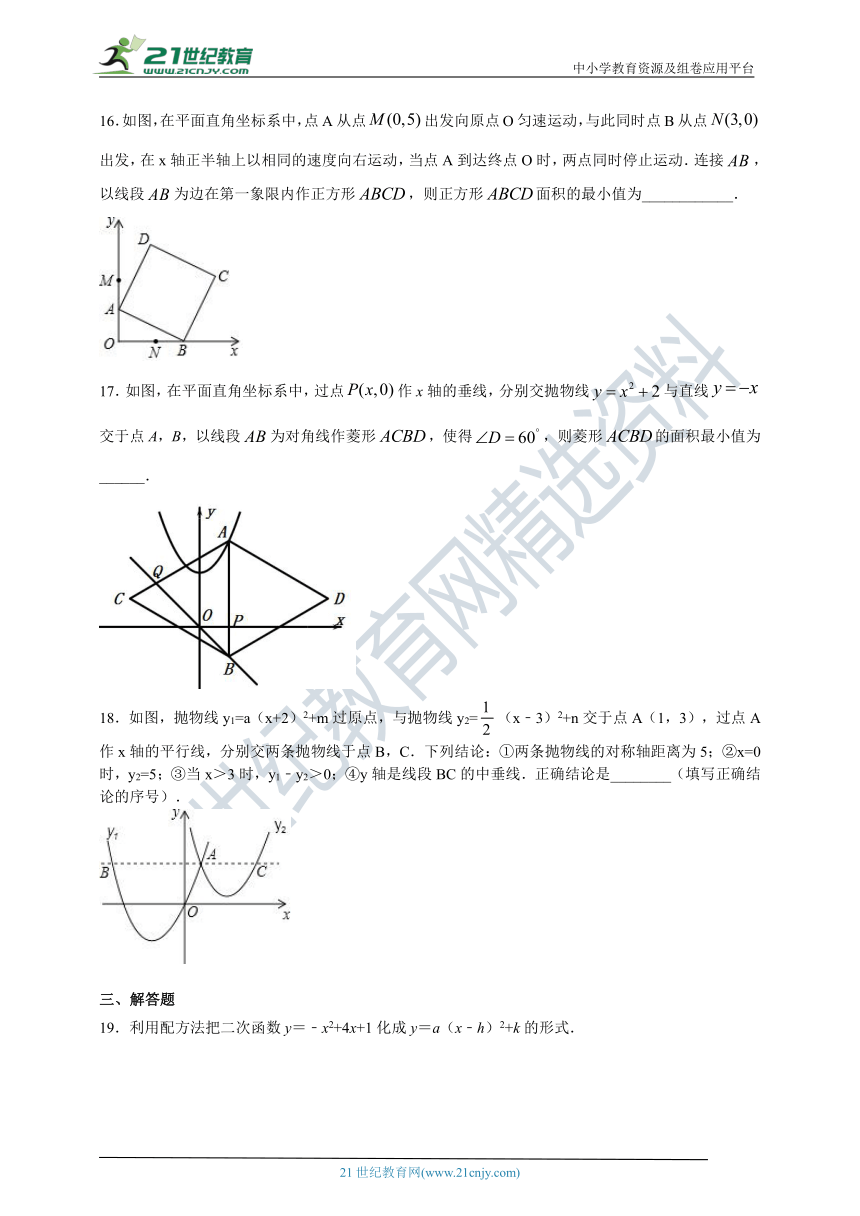
16.如图,在平面直角坐标系中,点A从点出发向原点O匀速运动,与此同时点B从点出发,在x轴正半轴上以相同的速度向右运动,当点A到达终点O时,两点同时停止运动.连接,以线段为边在第一象限内作正方形,则正方形面积的最小值为____________.
17.如图,在平面直角坐标系中,过点作x轴的垂线,分别交抛物线与直线交于点A,B,以线段为对角线作菱形,使得,则菱形的面积最小值为______.
18.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).
三、解答题
19.利用配方法把二次函数y=﹣x2+4x+1化成y=a(x﹣h)2+k的形式.
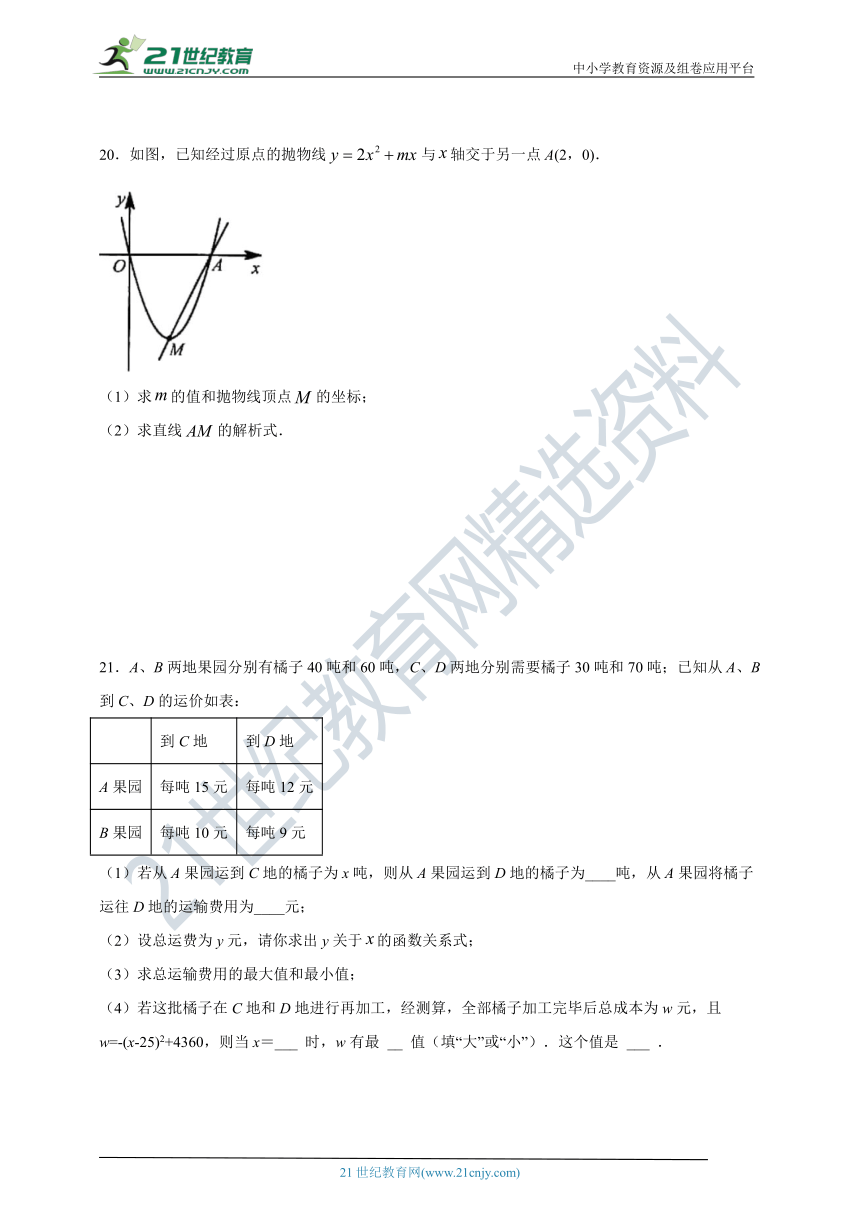
20.如图,已知经过原点的抛物线与轴交于另一点A(2,0).
(1)求的值和抛物线顶点的坐标;
(2)求直线的解析式.
21.A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:
到C地 到D地
A果园 每吨15元 每吨12元
B果园 每吨10元 每吨9元
(1)若从A果园运到C地的橘子为x吨,则从A果园运到D地的橘子为____吨,从A果园将橘子运往D地的运输费用为____元;
(2)设总运费为y元,请你求出y关于的函数关系式;
(3)求总运输费用的最大值和最小值;
(4)若这批橘子在C地和D地进行再加工,经测算,全部橘子加工完毕后总成本为w元,且w=-(x-25)2+4360,则当x=___ 时,w有最 __ 值(填“大”或“小”).这个值是 ___ .
22.在平面直角坐标系xOy中,抛物线y=ax2+bx经过点(3,3).
(1)用含a的式子表示b;
(2)直线y=x+4a+4与直线y=4交于点B,求点B的坐标(用含a的式子表示);
(3)在(2)的条件下,已知点A(1,4),若抛物线与线段AB恰有一个公共点,直接写出a(a<0)的取值范围.
23.如图,二次函数的图象与x轴相交于A,C两点(点A在点C的左侧),与y轴交于点B,点D为线段上一点(不与点O,C重合),以为边向上作正方形,连接,设点D的横坐标为m.
(1)当时,______,
当时,_______,
当时,________;
(2)根据(1)中的结果,猜想的大小,并证明你的猜想;
(3)当时,在坐标平面内有一点P,其横坐标为n,当以A,B,E,P为顶点的四边形为平行四边形时,请直接写出m与n满足的关系式.
参考答案
1.B
【详解】
解:∵抛物线y=5(x﹣6)2﹣2,
∴该抛物线的顶点坐标为(6,﹣2),
2.D
【详解】
解:∵在二次函数中,a=2>0,顶点坐标为(4,6),
∴函数有最小值为6.
3.D
【详解】
解:∵y=a(x-m)2(a<0),
∴抛物线开口向下,对称轴为直线x=m,
∴当抛物线上的点与直线x=m的距离越小,对应的y值就越大,
∵A(-1,p),B(3,q),且p<q,
∴B点到直线x=m的距离小于A点到直线x=m的距离,
∴m≥3,或m+1>3-m,
解得m>1,
而只有>1,
4.B
【详解】
解:设C1和Cn的顶点所在直线解析式为y=kx+b,
∵C1和Cn的顶点的连线平行于直线y=10x,
∴k=10,y=10x+b,
抛物线y=(x-n)2+n2的顶点坐标为(n,n2),
当n=1时,顶点为(1,1),
将(1,1)代入y=10x+b,
解得b=-9,
∴y=10x-9,
将(n,n2)代入解析时可得:n2=10n-9,
解得n=1(不合题意舍去)或n=9,
∴n=9.
5.C
【详解】
解:二次函数的对称轴为:
,且开口向上,
距离对称轴越近,函数值越小,
,
A,若,则不一定成立,故选项错误,不符合题意;
B,若,则不一定成立,故选项错误,不符合题意;
C,若,所以,则一定成立,故选项正确,符合题意;
D,若,则不一定成立,故选项错误,不符合题意;
6.A
【详解】
解:∵
∴该函数的对称轴为x=-1
∴当x<-1,y随x的增大而增大;当x>-1,y随x的增大而减小;且距x=-1距离越远,y越小
∵-1<1<2
∴y1>y2
∵|-1-(-2)|=1<|-1-1|=2
∴y3>y1
∴.
7.B
【分析】
将x=1代入抛物线解析式,得到C1的顶点坐标为(1,1),设直线的解析式为+b,将点C1的坐标(1,1)代入求出直线的解析式为-9,再将Cn的顶点坐标为(n,)代入,求出n的值即可.
【详解】
解:当x=1时,抛物线C1的顶点坐标为(1,1)
∵和的顶点的连线平行于直线,
∴设直线的解析式为+b,将点C1的坐标(1,1)代入,得10+b=1,
解得b=-9,
∴直线的解析式为-9,
将抛物线Cn的顶点坐标为(n,)代入,得,
解得n=1或n=9
8.A
【详解】
解:点的坐标为,点的坐标为,
,
抛物线、为常数)与线段交于、两点,且,
设点的坐标为,则点的坐标为,,
抛物线,
解得,.
9.B
【详解】
解:连接PM、PN.
∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠MPN=60°+30°=90°,
设PA=2a,则PB=8-2a,PM=a,,
∴ ,
∴当 时,点M,N之间的距离最短,最短距离为 ,
10.A
【详解】
解:设正方形ABCD的边长为m,则m>0,
∵DH=x,DH=AE=BF=CG
∴CG=x, CH=m-x,
∴
∵四边形的面积为=
∴y=
∴y与x的函数图像是A;
11.A
【详解】
由二次函数y=x2+k得抛物线开口向上,排除B;
根据一次函数y=﹣kx+2,得直线与y轴的正半轴相交,交点为(0,2),排除D;
根据A、C可知,抛物线交y轴于负半轴,所以k<0,故选A.
【点睛】
本题为判断一次函数与二次函数图象问题,关键是明确各个系数与二次函数与一次函数图象的关系.
12.B
【详解】
抛物线y1=(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),
∴3=a(1-4)2-3,
解得:a=,故①正确;
过点E作EF⊥AC于点F,
∵E是抛物线的顶点,
∴AE=EC,E(4,-3),
∴AF=3,EF=6,
∴AE=,AC=2AF=6,
∴AC≠AE,故②错误;
当y=3时,3=(x+1)2+1,
解得:x1=1,x2=-3,
故B(-3,3),D(-1,1),
则AB=4,AD=BD=2,
∴AD2+BD2=AB2,
∴③△ABD是等腰直角三角形,正确;
∵(x+1)2+1=(x-4)2-3时,
解得:x1=1,x2=37,
∴当37>x>1时,y1>y2,故④错误.
13.(﹣1,﹣3)
【详解】
解:抛物线y=﹣2(x+1)2﹣3的顶点坐标是(﹣1,﹣3).
故答案为:(﹣1,﹣3).
14.
【详解】
解:在二次函数,对称轴,
在图象上的三点,,,,,
,
则、、的大小关系为:.
故答案为:.
15.y=?4x2+16x?13或y=4x2?16x+19.
【分析】
根据二次函数的顶点坐标可设二次函数的解析式为y=a(x?2)2+3,由形状与抛物线y=4x2相同可得出|a|=4,代入后展开即可得出结论.
【详解】
解:∵二次函数的图象顶点坐标为(2,3),
∴设二次函数的解析式为y=a(x?2)2+3.
∵形状与抛物线y=4x2相同,
∴|a|=4,
∴该二次函数解析式为y=?4(x?2)2+3或y=4(x?2)2+3,
即y=?4x2+16x?13或y=4x2?16x+19.
故答案为:y=?4x2+16x?13或y=4x2?16x+19.
16.32
【详解】
解:由题意可得,NB=MA,则AO+OB=8,
设AO=x,则OB=8-x,
∵S正方形ABCD=AB2=AO2+OB2=x2+(8-x)2=2(x-4)2+32,
∴当x=4时,正方形ABCD的面积取得最小值32,
17.
【分析】
如图,连接交于点M,过点作x轴的垂线,分别交抛物线与直线于A,B两点,得出,可得,即可求出当时,的最小值为.根据,四边形为菱形,得出为等边三角形,,且与互相平分,求出,.根据勾股定理求出DM,即可求出CD,即可求出菱形的面积最小值.
【详解】
如图,连接交于点M.
∵过点作x轴的垂线,分别交抛物线与直线于A,B两点,
∴.
∴,
∴当时,的最小值为.
∵,四边形为菱形,
∴为等边三角形,,且与互相平分,
∴,.
在中,,
∴,
∴菱形的面积最小值为,
知识点灵活运用是解题关键.
18.①③④
【详解】
∵抛物线y1=a(x+2)2+m与抛物线y2=(x﹣3)2+n的对称轴分别为x=-2,x=3,
∴两条抛物线的对称轴距离为5,故①正确;
∵抛物线y2=(x﹣3)2+n交于点A(1,3),
∴2+n=3,即n=1;
∴y2=(x﹣3)2+1,
把x=0代入y2=(x﹣3)2+1得,y=≠5,②错误;
由图象可知,当x>3时,y1>y2,∴x>3时,y1﹣y2>0,③正确;
∵抛物线y1=a(x+2)2+m过原点和点A(1,3),
∴,
解得 ,
∴.
令y1=3,则,
解得x1=-5,x2=1,
∴AB=1-(-5)=6,
∴A(1,3),B(-5,3);
令y2=3,则(x﹣3)2+1=3,
解得x1=5,x2=1,
∴C(5,3),
∴AC=5-1=4,
∴BC=10,
∴y轴是线段BC的中垂线,故④正确.
19.
【详解】
解:
所以把二次函数化成的形式为:.
20.(1),M (1,-2);(2)
【详解】
解 (1)∵抛物线过点A(2,0),
,解得,
,
,
∴顶点M的坐标是(1,-2);
(2)设直线AM的解析式为,
∵图象过A(2,0),M (1,-2),
,解得,
∴直线AM的解析式为.
21.(1)(40-x),12(40-x);(2)y=2x+1050;(3)最大值为1110元,最小值为1050元;(4)25,大,4360
【分析】
(1)因为从A果园运到C地的橘子是x吨,剩下的都运往D地,所以运往D地的是(40-x)吨.运输费用=吨数×每吨的运费.
(2)总运费=从A运往C、D的费用+从B运往C、D的费用.
(3)总运费与x是一次函数关系,由于0≤x≤30,可计算出总运费的最大值和最小值.
(4)利用二次函数的性质,求出函数的最值.
【详解】
解:(1)因为从A果园运到C地的橘子是x吨,那么从A果园运到D地的橘子为(40-x)吨,
从A运到D地的运费是12元每吨,所以A果园将橘子运往D地的运输费用为12(40-x)吨.
故答案为:(40-x),12(40-x);
(2)从A果园运到C地x吨,运费为每吨15元;从A果园运到D地的橘子为(40-x)吨,运费为每吨12元;
从B果园运到C地(30-x)吨,运费为每吨10元;从B果园运到D地(30+x)吨,运费为每吨9元;
所以总运费为:y=15x+12(40-x)+10(30-x)+9(30+x)
=2x+1050;
(3)因为总运费y =2x+1050,
∵,
∴函数值随x的增大而增大,
由于0≤x≤30,
∴当x=30时,有最大值2×30+1050=1110元,
当x=0时,有最小值2×0+1050=1050元;
(4)w=-(x-25)2+4360,
∵二次项系数-1<0,
∴抛物线开口向下,
当x=25时,w有最大值.最大值时4360.
故答案为:25,大,4360.
22.(1)b=﹣3a+1;(2)B(﹣4a,4);(3)a=﹣1或a<﹣
【分析】
(1)将点(3,3)代入解析式即可求解;
(2)把y=4代入y=x+4a+4得到关于x的方程,解方程即可求出B点坐标;
(3)根据抛物线与线段AB恰有一个公共点,分两种情况进行讨论,即可得到结论.
【详解】
解:(1)将点(3,3)代入y=ax2+bx,得:9a+3b=3,
∴b=-3a+1;
(2)令x+4a+4=4,得x=-4a,
∴B(-4a,4),
(3)∵a<0,
∴抛物线开口向下,
∵A(1,4),B(-4a,4),
∴点A、B所在的直线为y=4,
由(1)得b=1-3a,
则抛物线可化为:y=ax2+(1-3a)x,
当抛物线与线段AB恰有一个公共点时,分两种情况讨论:
①当抛物线y=ax2+(1﹣3a)x与直线y=4只有一个公共点且抛物线的顶点在点A、B之间时,
则或,
方程ax2+(1﹣3a)x=4的根的判别式:△=0,
即(1﹣3a)2+16a=0,
解得a1=,a2=,
当a1=时,(不符合题意),
当a2=﹣1时,,则1≤≤-4a成立,
②当抛物线经过点A时,
即当x=1,y=4时,a+1-3a=4,
解得a=;
∴a<时,抛物线与线段AB恰有一个公共点,
综上所述,当a=-1或a<-时,抛物线与线段AB恰有一个公共点.
23.(1);8;;(2).证明见解析;(3)当以A,B,E,P为顶点的四边形为平行四边形时,m与n满足的关系式有和.
【分析】
(1)令,解得,求出点A的坐标为,令,求出点B的坐标为,再表示出D,E的坐标,再根据k,m的值代入求出坐标,再利用割补法即可求解面积;
(2)把k,m当做常数,利用割补法即可求出;
(3)根据,求出,再根据平行四边形的性质分三种情况讨论即可求解.
【详解】
(1)令,
解得,
∴点A的坐标为.
令,则,
∴点B的坐标为.
∵点D的横坐标为m,
∴点E的坐标为,点D的坐标为.
当时,,
;
当时,,
;
当时,,
.
故答案为;8;.
(2).证明:由(1)知,
.
(3)设点P的坐标为.
∵,∴.
当以A,B,E,P为顶点的四边形为平行四边形时,分三种情况:
①当为对角线时,令对角线的交点为M,如图(1)所示.
∵四边形为平行四边形,
∴点M平分,点M平分.
∵,
∴,
即.
②当为对边,且点P在点E的左侧时,延长,过点P作延长线于点N,如图(2)所示.
∵四边形为平行四边形,
∴,且,
∵,
∴,即.
③当为对边,且点P在点E的右侧时,延长,过点P作于点N,如图(3)所示.
∵四边形为平行四边形,
∴,且,
∴.
∵.
∴,
即.
综上可知:当以A,B,E,P为顶点的四边形为平行四边形时,m与n满足的关系式有和.
_21?????????è?????(www.21cnjy.com)_
人教版2021年九年级上册数学同步练习卷
22.1二次函数的图像和性质
22.1.3 二次函数y=a(x-h)2+k的图像和性质
一、单选题
1.抛物线y=5(x﹣6)2﹣2的顶点坐标是( )
A.(6,2) B.(6,﹣2) C.(﹣6,2) D.(﹣6,﹣2)
2.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
3.已知二次函数的图象经过点,,若,则的值可能是( )
A. B. C.0 D.
4.如图,在平面直角坐标系中,有一系列的抛物线(为正整数),若和的顶点的连线平行于直线,则该条抛物线对应的的值是( )
A.8 B.9 C.10 D.11
5.二次函数的图象过四个点,下列说法一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.已知点在抛物线上,则下列结论正确的是( )
A. B. C. D.
7.如图,在平面直角坐标系中,有一系列的抛物线(为正整数),若和的顶点的连线平行于直线,则该条抛物线对应的的值是( )
A.8 B.9 C.11 D.10
8.在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,2),若抛物线y=(x﹣h)2+k(h、k为常数)与线段AB交于C、D两点,且CD=AB,则k的值为( )
A. B.2 C. D.
9.如图,已知,为线段上的一个动点,分别以,为边在的同侧作菱形和菱形,点,,在一条直线上,.,分别是对角线,的中点.当点在线段上移动时,点,之间的距离最短为( )
A. B. C.4 D.3
10.如图,点、、、是正方形四条边(不含端点)上的点,设线段的长为,四边形的面积为,则能够反映与之间函数关系的图象大致是( )
A. B. C.D.
11.在同一坐标中,一次函数y=﹣kx+2与二次函数y=x2+k的图象可能是( )
A. B.
C. D.
12.如图,抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:
①a=;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
其中正确的结论是( )
A.①③④ B.①③ C.①②④ D.②
二、填空题
13.抛物线y=﹣2(x+1)2﹣3的顶点坐标是_____.
14.在抛物线图象上有三点,则的大小关系是_______
15.已知一个二次函数的图象形状与抛物线相同,且顶点坐标为,则这个二次函数的解析式为_____________.
16.如图,在平面直角坐标系中,点A从点出发向原点O匀速运动,与此同时点B从点出发,在x轴正半轴上以相同的速度向右运动,当点A到达终点O时,两点同时停止运动.连接,以线段为边在第一象限内作正方形,则正方形面积的最小值为____________.
17.如图,在平面直角坐标系中,过点作x轴的垂线,分别交抛物线与直线交于点A,B,以线段为对角线作菱形,使得,则菱形的面积最小值为______.
18.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).
三、解答题
19.利用配方法把二次函数y=﹣x2+4x+1化成y=a(x﹣h)2+k的形式.
20.如图,已知经过原点的抛物线与轴交于另一点A(2,0).
(1)求的值和抛物线顶点的坐标;
(2)求直线的解析式.
21.A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:
到C地 到D地
A果园 每吨15元 每吨12元
B果园 每吨10元 每吨9元
(1)若从A果园运到C地的橘子为x吨,则从A果园运到D地的橘子为____吨,从A果园将橘子运往D地的运输费用为____元;
(2)设总运费为y元,请你求出y关于的函数关系式;
(3)求总运输费用的最大值和最小值;
(4)若这批橘子在C地和D地进行再加工,经测算,全部橘子加工完毕后总成本为w元,且w=-(x-25)2+4360,则当x=___ 时,w有最 __ 值(填“大”或“小”).这个值是 ___ .
22.在平面直角坐标系xOy中,抛物线y=ax2+bx经过点(3,3).
(1)用含a的式子表示b;
(2)直线y=x+4a+4与直线y=4交于点B,求点B的坐标(用含a的式子表示);
(3)在(2)的条件下,已知点A(1,4),若抛物线与线段AB恰有一个公共点,直接写出a(a<0)的取值范围.
23.如图,二次函数的图象与x轴相交于A,C两点(点A在点C的左侧),与y轴交于点B,点D为线段上一点(不与点O,C重合),以为边向上作正方形,连接,设点D的横坐标为m.
(1)当时,______,
当时,_______,
当时,________;
(2)根据(1)中的结果,猜想的大小,并证明你的猜想;
(3)当时,在坐标平面内有一点P,其横坐标为n,当以A,B,E,P为顶点的四边形为平行四边形时,请直接写出m与n满足的关系式.
参考答案
1.B
【详解】
解:∵抛物线y=5(x﹣6)2﹣2,
∴该抛物线的顶点坐标为(6,﹣2),
2.D
【详解】
解:∵在二次函数中,a=2>0,顶点坐标为(4,6),
∴函数有最小值为6.
3.D
【详解】
解:∵y=a(x-m)2(a<0),
∴抛物线开口向下,对称轴为直线x=m,
∴当抛物线上的点与直线x=m的距离越小,对应的y值就越大,
∵A(-1,p),B(3,q),且p<q,
∴B点到直线x=m的距离小于A点到直线x=m的距离,
∴m≥3,或m+1>3-m,
解得m>1,
而只有>1,
4.B
【详解】
解:设C1和Cn的顶点所在直线解析式为y=kx+b,
∵C1和Cn的顶点的连线平行于直线y=10x,
∴k=10,y=10x+b,
抛物线y=(x-n)2+n2的顶点坐标为(n,n2),
当n=1时,顶点为(1,1),
将(1,1)代入y=10x+b,
解得b=-9,
∴y=10x-9,
将(n,n2)代入解析时可得:n2=10n-9,
解得n=1(不合题意舍去)或n=9,
∴n=9.
5.C
【详解】
解:二次函数的对称轴为:
,且开口向上,
距离对称轴越近,函数值越小,
,
A,若,则不一定成立,故选项错误,不符合题意;
B,若,则不一定成立,故选项错误,不符合题意;
C,若,所以,则一定成立,故选项正确,符合题意;
D,若,则不一定成立,故选项错误,不符合题意;
6.A
【详解】
解:∵
∴该函数的对称轴为x=-1
∴当x<-1,y随x的增大而增大;当x>-1,y随x的增大而减小;且距x=-1距离越远,y越小
∵-1<1<2
∴y1>y2
∵|-1-(-2)|=1<|-1-1|=2
∴y3>y1
∴.
7.B
【分析】
将x=1代入抛物线解析式,得到C1的顶点坐标为(1,1),设直线的解析式为+b,将点C1的坐标(1,1)代入求出直线的解析式为-9,再将Cn的顶点坐标为(n,)代入,求出n的值即可.
【详解】
解:当x=1时,抛物线C1的顶点坐标为(1,1)
∵和的顶点的连线平行于直线,
∴设直线的解析式为+b,将点C1的坐标(1,1)代入,得10+b=1,
解得b=-9,
∴直线的解析式为-9,
将抛物线Cn的顶点坐标为(n,)代入,得,
解得n=1或n=9
8.A
【详解】
解:点的坐标为,点的坐标为,
,
抛物线、为常数)与线段交于、两点,且,
设点的坐标为,则点的坐标为,,
抛物线,
解得,.
9.B
【详解】
解:连接PM、PN.
∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠MPN=60°+30°=90°,
设PA=2a,则PB=8-2a,PM=a,,
∴ ,
∴当 时,点M,N之间的距离最短,最短距离为 ,
10.A
【详解】
解:设正方形ABCD的边长为m,则m>0,
∵DH=x,DH=AE=BF=CG
∴CG=x, CH=m-x,
∴
∵四边形的面积为=
∴y=
∴y与x的函数图像是A;
11.A
【详解】
由二次函数y=x2+k得抛物线开口向上,排除B;
根据一次函数y=﹣kx+2,得直线与y轴的正半轴相交,交点为(0,2),排除D;
根据A、C可知,抛物线交y轴于负半轴,所以k<0,故选A.
【点睛】
本题为判断一次函数与二次函数图象问题,关键是明确各个系数与二次函数与一次函数图象的关系.
12.B
【详解】
抛物线y1=(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),
∴3=a(1-4)2-3,
解得:a=,故①正确;
过点E作EF⊥AC于点F,
∵E是抛物线的顶点,
∴AE=EC,E(4,-3),
∴AF=3,EF=6,
∴AE=,AC=2AF=6,
∴AC≠AE,故②错误;
当y=3时,3=(x+1)2+1,
解得:x1=1,x2=-3,
故B(-3,3),D(-1,1),
则AB=4,AD=BD=2,
∴AD2+BD2=AB2,
∴③△ABD是等腰直角三角形,正确;
∵(x+1)2+1=(x-4)2-3时,
解得:x1=1,x2=37,
∴当37>x>1时,y1>y2,故④错误.
13.(﹣1,﹣3)
【详解】
解:抛物线y=﹣2(x+1)2﹣3的顶点坐标是(﹣1,﹣3).
故答案为:(﹣1,﹣3).
14.
【详解】
解:在二次函数,对称轴,
在图象上的三点,,,,,
,
则、、的大小关系为:.
故答案为:.
15.y=?4x2+16x?13或y=4x2?16x+19.
【分析】
根据二次函数的顶点坐标可设二次函数的解析式为y=a(x?2)2+3,由形状与抛物线y=4x2相同可得出|a|=4,代入后展开即可得出结论.
【详解】
解:∵二次函数的图象顶点坐标为(2,3),
∴设二次函数的解析式为y=a(x?2)2+3.
∵形状与抛物线y=4x2相同,
∴|a|=4,
∴该二次函数解析式为y=?4(x?2)2+3或y=4(x?2)2+3,
即y=?4x2+16x?13或y=4x2?16x+19.
故答案为:y=?4x2+16x?13或y=4x2?16x+19.
16.32
【详解】
解:由题意可得,NB=MA,则AO+OB=8,
设AO=x,则OB=8-x,
∵S正方形ABCD=AB2=AO2+OB2=x2+(8-x)2=2(x-4)2+32,
∴当x=4时,正方形ABCD的面积取得最小值32,
17.
【分析】
如图,连接交于点M,过点作x轴的垂线,分别交抛物线与直线于A,B两点,得出,可得,即可求出当时,的最小值为.根据,四边形为菱形,得出为等边三角形,,且与互相平分,求出,.根据勾股定理求出DM,即可求出CD,即可求出菱形的面积最小值.
【详解】
如图,连接交于点M.
∵过点作x轴的垂线,分别交抛物线与直线于A,B两点,
∴.
∴,
∴当时,的最小值为.
∵,四边形为菱形,
∴为等边三角形,,且与互相平分,
∴,.
在中,,
∴,
∴菱形的面积最小值为,
知识点灵活运用是解题关键.
18.①③④
【详解】
∵抛物线y1=a(x+2)2+m与抛物线y2=(x﹣3)2+n的对称轴分别为x=-2,x=3,
∴两条抛物线的对称轴距离为5,故①正确;
∵抛物线y2=(x﹣3)2+n交于点A(1,3),
∴2+n=3,即n=1;
∴y2=(x﹣3)2+1,
把x=0代入y2=(x﹣3)2+1得,y=≠5,②错误;
由图象可知,当x>3时,y1>y2,∴x>3时,y1﹣y2>0,③正确;
∵抛物线y1=a(x+2)2+m过原点和点A(1,3),
∴,
解得 ,
∴.
令y1=3,则,
解得x1=-5,x2=1,
∴AB=1-(-5)=6,
∴A(1,3),B(-5,3);
令y2=3,则(x﹣3)2+1=3,
解得x1=5,x2=1,
∴C(5,3),
∴AC=5-1=4,
∴BC=10,
∴y轴是线段BC的中垂线,故④正确.
19.
【详解】
解:
所以把二次函数化成的形式为:.
20.(1),M (1,-2);(2)
【详解】
解 (1)∵抛物线过点A(2,0),
,解得,
,
,
∴顶点M的坐标是(1,-2);
(2)设直线AM的解析式为,
∵图象过A(2,0),M (1,-2),
,解得,
∴直线AM的解析式为.
21.(1)(40-x),12(40-x);(2)y=2x+1050;(3)最大值为1110元,最小值为1050元;(4)25,大,4360
【分析】
(1)因为从A果园运到C地的橘子是x吨,剩下的都运往D地,所以运往D地的是(40-x)吨.运输费用=吨数×每吨的运费.
(2)总运费=从A运往C、D的费用+从B运往C、D的费用.
(3)总运费与x是一次函数关系,由于0≤x≤30,可计算出总运费的最大值和最小值.
(4)利用二次函数的性质,求出函数的最值.
【详解】
解:(1)因为从A果园运到C地的橘子是x吨,那么从A果园运到D地的橘子为(40-x)吨,
从A运到D地的运费是12元每吨,所以A果园将橘子运往D地的运输费用为12(40-x)吨.
故答案为:(40-x),12(40-x);
(2)从A果园运到C地x吨,运费为每吨15元;从A果园运到D地的橘子为(40-x)吨,运费为每吨12元;
从B果园运到C地(30-x)吨,运费为每吨10元;从B果园运到D地(30+x)吨,运费为每吨9元;
所以总运费为:y=15x+12(40-x)+10(30-x)+9(30+x)
=2x+1050;
(3)因为总运费y =2x+1050,
∵,
∴函数值随x的增大而增大,
由于0≤x≤30,
∴当x=30时,有最大值2×30+1050=1110元,
当x=0时,有最小值2×0+1050=1050元;
(4)w=-(x-25)2+4360,
∵二次项系数-1<0,
∴抛物线开口向下,
当x=25时,w有最大值.最大值时4360.
故答案为:25,大,4360.
22.(1)b=﹣3a+1;(2)B(﹣4a,4);(3)a=﹣1或a<﹣
【分析】
(1)将点(3,3)代入解析式即可求解;
(2)把y=4代入y=x+4a+4得到关于x的方程,解方程即可求出B点坐标;
(3)根据抛物线与线段AB恰有一个公共点,分两种情况进行讨论,即可得到结论.
【详解】
解:(1)将点(3,3)代入y=ax2+bx,得:9a+3b=3,
∴b=-3a+1;
(2)令x+4a+4=4,得x=-4a,
∴B(-4a,4),
(3)∵a<0,
∴抛物线开口向下,
∵A(1,4),B(-4a,4),
∴点A、B所在的直线为y=4,
由(1)得b=1-3a,
则抛物线可化为:y=ax2+(1-3a)x,
当抛物线与线段AB恰有一个公共点时,分两种情况讨论:
①当抛物线y=ax2+(1﹣3a)x与直线y=4只有一个公共点且抛物线的顶点在点A、B之间时,
则或,
方程ax2+(1﹣3a)x=4的根的判别式:△=0,
即(1﹣3a)2+16a=0,
解得a1=,a2=,
当a1=时,(不符合题意),
当a2=﹣1时,,则1≤≤-4a成立,
②当抛物线经过点A时,
即当x=1,y=4时,a+1-3a=4,
解得a=;
∴a<时,抛物线与线段AB恰有一个公共点,
综上所述,当a=-1或a<-时,抛物线与线段AB恰有一个公共点.
23.(1);8;;(2).证明见解析;(3)当以A,B,E,P为顶点的四边形为平行四边形时,m与n满足的关系式有和.
【分析】
(1)令,解得,求出点A的坐标为,令,求出点B的坐标为,再表示出D,E的坐标,再根据k,m的值代入求出坐标,再利用割补法即可求解面积;
(2)把k,m当做常数,利用割补法即可求出;
(3)根据,求出,再根据平行四边形的性质分三种情况讨论即可求解.
【详解】
(1)令,
解得,
∴点A的坐标为.
令,则,
∴点B的坐标为.
∵点D的横坐标为m,
∴点E的坐标为,点D的坐标为.
当时,,
;
当时,,
;
当时,,
.
故答案为;8;.
(2).证明:由(1)知,
.
(3)设点P的坐标为.
∵,∴.
当以A,B,E,P为顶点的四边形为平行四边形时,分三种情况:
①当为对角线时,令对角线的交点为M,如图(1)所示.
∵四边形为平行四边形,
∴点M平分,点M平分.
∵,
∴,
即.
②当为对边,且点P在点E的左侧时,延长,过点P作延长线于点N,如图(2)所示.
∵四边形为平行四边形,
∴,且,
∵,
∴,即.
③当为对边,且点P在点E的右侧时,延长,过点P作于点N,如图(3)所示.
∵四边形为平行四边形,
∴,且,
∴.
∵.
∴,
即.
综上可知:当以A,B,E,P为顶点的四边形为平行四边形时,m与n满足的关系式有和.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
