22.1.4 二次函数y=ax2+bx+k的图像和性质 课时达标检测(含解析)
文档属性
| 名称 | 22.1.4 二次函数y=ax2+bx+k的图像和性质 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 21:53:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年九年级上册数学同步练习卷
22.1二次函数的图像和性质
22.1.4 二次函数y=ax2+bx+k的图像和性质
一、单选题
1.二次函数的最小值为( )
A.-1 B.1 C.2 D.3
2.将抛物线向右平移1个单位,得到抛物线表达式为( )
A. B. C. D.
3.已知二次函数,当时,,则的值是( )
A.3 B.4 C.6 D.7
4.函数的图像可以由函数的图像通过如下平移得到( )
A.向左平移1个单位,再向上平移1个单位
B.向左平移1个单位,再向下平移1个单位
C.向右平移2个单位,再向上平移1个单位
D.向右平移2个单位,再向下平多1个单位
5.若坐标平面上二次函数的图形,经过平移后可与的图形完全叠合,则a、b、c的值可能为下列哪一组?( )
A.,, B.,,
C.,, D.,,
6.已知抛物线上的部分点的横坐标x与纵坐标y的对应值如表:
x … -1 0 1 2 3 …
y … 3 0 -1 m 3 …
以下结论正确的是( )
A.抛物线的开口向下
B.当时,y随x增大而增大
C.方程的根为0和2
D.当时,x的取值范围是
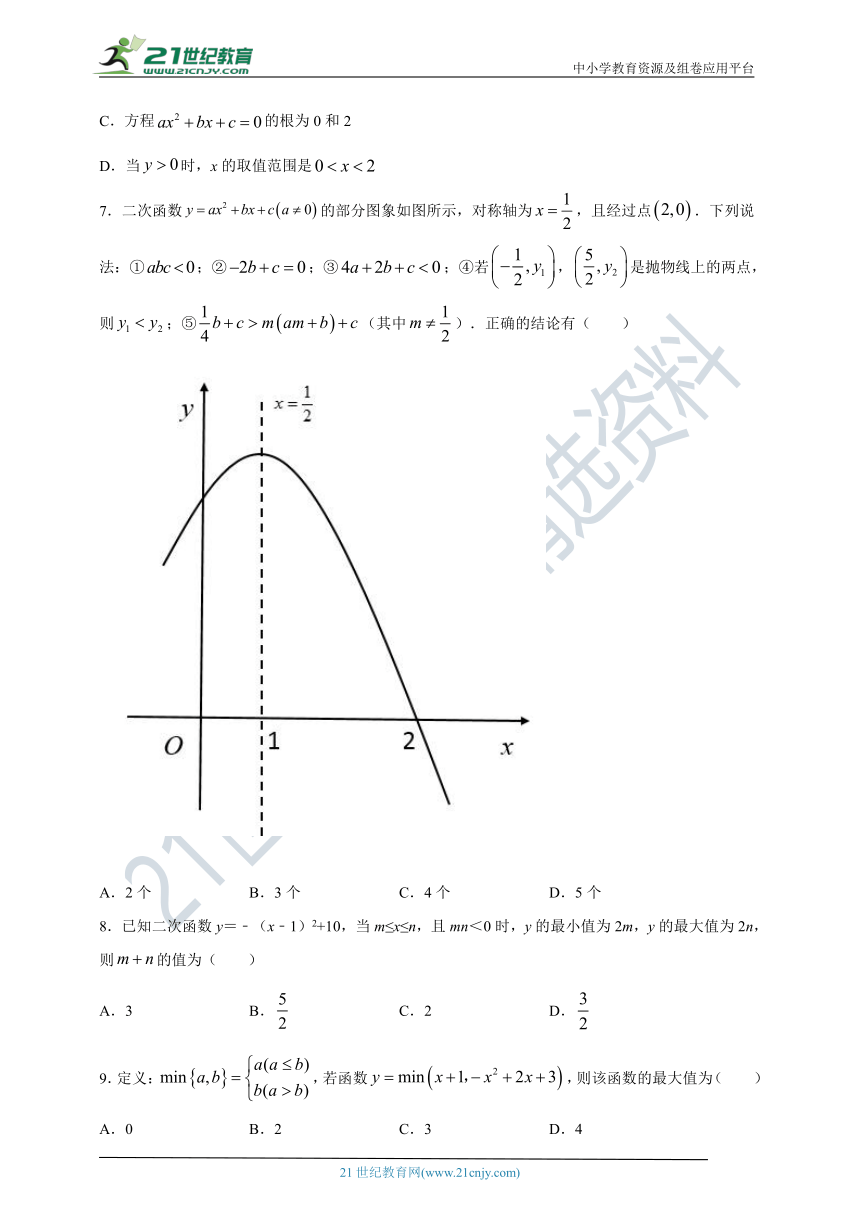
7.二次函数的部分图象如图所示,对称轴为,且经过点.下列说法:①;②;③;④若,是抛物线上的两点,则;⑤(其中).正确的结论有( )
A.2个 B.3个 C.4个 D.5个
8.已知二次函数y=﹣(x﹣1)2+10,当m≤x≤n,且mn<0时,y的最小值为2m,y的最大值为2n,则的值为( )
A.3 B. C.2 D.
9.定义:,若函数,则该函数的最大值为( )
A.0 B.2 C.3 D.4
10.如图,抛物线交轴分别于点,,交轴正半轴于点,抛物线顶点为.下列结论:①;②;③当时,;④当是等腰直角三角形时,;⑤点是抛物线对称轴上的一点,若,则周长的最小值为.其中,正确的个数为( )
A.2个 B.3个 C.4个 D.5个
11.已知二次函数与x轴交于A,B两点,与y轴交于点C.下列说法正确的是( )
①线段的长度为;②抛物线的对称轴为直线;③P是此抛物线的对称轴上的一个动点,当P点坐标为时,的值最大;④若M是x轴上的一个动点,N是此抛物线上的一个动点,如果以A,C,M,N为顶点的四边形是平行四边形,满足条件的M点有4个.
A.①② B.①②③ C.①②④ D.③④
12.如图,A(0,1),B(1,5),曲线BC是双曲线的一部分.曲线AB与BC组成图形G .由点C开始不断重复图形G形成一线“波浪线”.若点P(2020,m) ,Q( x,n )在该“波浪线”上,则m的值为 ,n的最大值为 ( )
A.m = 1,n = 1 B.m = 5,n = 1 C.m = 1,n = 5 D.m = 1,n = 4
二、填空题
13.二次函数的图象开口方向是_______(填“向上”或“向下”).
14.已知函数的部分图像如图所示,那么当x________时,y随x的增大而增大.
15.某校建一个新球场到了最后画线阶段,已知甲在乙的正北50米处沿正东方向以3米/秒的速度画线,同时乙沿正北方向以1米/秒的速度画线,经过___________秒后两人的距离最短.
16.已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象如图所示,下面四个结论,①abc<0;②a+c<b;③2a+b=1;④a+b≥m(am+b),其中全部正确的是______
17.对某一个函数给出如下定义:若存在实数,对于任意的函数值,都满足,则称这个函数是有界函数,在所有满足条件的中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.将函数的图象向上平移个单位,得到的函数的边界值满足是时,则的取值范围是______.
18.如图,已知点,,两点,在抛物线上,向左或向右平移抛物线后,,的对应点分别为,,当四边形的周长最小时,抛物线的解析式为__________.
三、解答题
19.已知二次函数经过求二次函数的表达式.
20.如图,抛物线与轴交于点和点,与轴交于点,连接,与抛物线的对称轴交于点,顶点为点.
(1)求抛物线的解析式;
(2)求的面积.
21.设二次函数y=x2﹣2(m+1)x+3﹣m,其中m是实数.
(1)若函数的图象经过点(﹣2,8),求此函数的表达式;
(2)若x>0时,y随x的增大而增大,求m的最大值.
(3)已知A(﹣1,3),B(2,3),若该二次函数的图象与线段AB只有一个交点(不包括A,B两个端点),求m的取值范围.
22.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B的左侧),经过点A的直线与y轴负半轴交于点C,与抛物线交于另一点D.
(1)则点D的坐标为_______(用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若面积的最大值为,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A、D、P、Q为顶点的四边形成为矩形时,求出点P的坐标.
23.在平面直角坐标系中,抛物线(m为常数).
(1)当点在该抛物线上时,求m的值.
(2)将抛物线在的部分图象沿y轴翻折得到新图象记为G,当时,图象G的函数值y先随x的增大而增大,后随x的增大而减小,求m的取值范围.
(3)当该抛物线在的部分图象的最高点到的距离为1时,求m的值.
(4)当时,过点作垂直于x轴的直线交该抛物线于点B,在AB延长上取一点C,使,将线段AB绕点A顺时针旋转得到线段AE,以AC、AE为邻边作矩形ACDE,当该抛物线的顶点在矩形的边上时,直接写出该抛物线在该矩形内部(包含边界)图象所对应的函数的最大值与最小值的差.
参考答案
1.C
【详解】
解:当时,二次函数有最小值,
且最小值为:,
2.C
【详解】
解:二次函数y=2x2的图象向右平移1个单位,
得:y=2(x-1)2.
3.C
【详解】
∵
∴该函数的对称轴是直线x=3,函数图象开口向上,
当x=3时取得最小值-1,
又∵时,
当x=0时,y=8,当x=6时,y=8,
∴m=6
4.C
【详解】
函数的图像可以由函数的图像通过右平移2个单位,再向上平移1个单位.
5.A
【详解】
解:二次函数的图形,经过平移后可与的图形完全叠合,
.
故选:A.
6.C
利用表中数据求出抛物线的解析式,根据解析式依次进行判断.
【详解】
解:将代入抛物线的解析式得;
,
解得:,
所以抛物线的解析式为:,
A、,抛物线开口向上,故选项错误,不符合题;
B、抛物线的对称轴为直线,在时,y随x增大而增大,故选项错误,不符合题意;
C、方程的根为0和2,故选项正确,符合题意;
D、当时,x的取值范围是或,故选项错误,不符合题意;
7.B
【详解】
解:抛物线的开口向下,与轴的交点位于轴正半轴,
,
抛物线的对称轴为,
,
,则结论①正确;
将点代入二次函数的解析式得:,则结论③错误;
将代入得:,则结论②正确;
抛物线的对称轴为,
和时的函数值相等,即都为,
又当时,随的增大而减小,且,
,则结论④错误;
由函数图象可知,当时,取得最大值,最大值为,
,
,
即,结论⑤正确;
综上,正确的结论有①②⑤,共3个,
8.C
【详解】
解:二次函数y=﹣(x﹣1)2+10的大致图象如下:
.
∵mn<0时,y的最小值为2m,y的最大值为2n,
∴m<0,n>0,
①当n<1时,x=m时,y取最小值,即2m=﹣(m﹣1)2+10,
解得:m=﹣3.
当x=n时,y取最大值,即2n=﹣(n﹣1)2+10,
解得:n=3或n=﹣3(均不合题意,舍去);
②当n≥1时,当x=m时,y取最小值,即2m=﹣(m﹣1)2+10,
解得:m=﹣3.
当x=1时,y取最大值,即2n=﹣(1﹣1)2+10,
解得:n=5,
或x=n时,y取最小值,x=1时,y取最大值,
2m=﹣(n﹣1)2+10,n=5,
∴m=﹣3,
所以m+n=﹣3+5=2.
9.C
【详解】
令,
当时,即时,,
令 ,则w与x轴的交点坐标为(2,0),(-1,0),
∴当时,,
∴(),
∵y随x的增大而增大,
∴当x=2时,;
当时,即时,,
令 ,则w与x轴的交点坐标为(2,0),(-1,0),
∴当时,或,
∴(或),
∵的对称轴为x=1,
∴当时,y随x的增大而减小,
∵当x=2时,=3,
∴当时,y<3;
当,y随x的增大而增大,
∴当x=-1时,=0;
∴当时,y<0;
综上,的最大值为3.
10.D
【详解】
解:把点,,代入得到,
消去得到,故①,②正确,
∵抛物线的对称轴,开口向下,
∴时,有最大值,最大值,
∵,
∴,
∴,故③正确,
当是等腰直角三角形时,,
可以假设抛物线的解析式为,把(1,0)代入得到,故④正确,
如图,连接交抛物线的对称轴于,连接,此时的周长最小,
最小值,
∵,,
∴△PBD周长最小值为,故⑤正确.
11.C
【详解】
解:在中,
令x=0,则y=2,
令y=0,则,
解得x=或2,
∴A(,0),C(0,2),
∴AC=,①正确;
∵,
∴抛物线的对称轴为直线,②正确;
延长AC,与对称轴交于点P,此时的值最大,
∵A(,0),C(0,2),设直线AC的表达式为:y=mx+n,
则,解得:,
∴直线AC的表达式为y=4x+2,
令,则y=5,
∴当点P的坐标为(,5)时,的值最大,③错误;
如图,若以A,C,M,N为顶点的四边形是平行四边形,
当AC为边时,有ACM1N1,ACM2N2,ACM3N3,共3个平行四边形,
当AC为对角线时,有AMCN1,共1个平行四边形,
∴符合条件的点M有4个,④正确,
故选C.
12.C
【详解】
解:∵点B(1,5)在双曲线的图象上,
∴k=5,
∵A(0,1),曲线AB与BC组成图形G .由点C开始不断重复图形G形成一线“波浪线”.
∴C的纵坐标为1
∵点C在的图象上,点C的纵坐标为1,
∴点C的横坐标是5,
∴点C的坐标为(5,1),
∵2020÷5=404,
∴P(2020,m)中m=1
∵点Q(x,n)在该“波浪线”上,
∴n的最大值是5.
综上所述,m = 1,n = 5.
13.向上
【详解】
解:∵二次函数,a=1>0,
∴二次函数的图象开口方向向上,
故答案是:向上.
14.<1
【详解】
解:根据图象得:
函数图像开口向下,对称轴为直线x=1,
∴当x<1时,y随x的增大而增大,
15.5
【详解】
解:设t秒时甲乙两者间的距离最短,
依题意得AD=3tm,BA=50m,BC=tm,AC=(50-t)m,
在Rt△ADC中
由勾股定理得CD=,
,
,
,
当t=5时CD最短.
16.①②④.
【详解】
解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴a,b异号,b>0,
∵抛物线与y轴交点在y轴正半轴,
∴c>0,
∴abc<0,
故①正确;
由图象得当x=-1时,y=a-b+c<0,
∴a+c<b,
故②正确;
∵图象对称轴为直线x==1,
∴﹣b=2a,即2a+b=0,
故③错误;
由a+b≥m(am+b)得a+b+c≥am2+bm+c,
∵x=1时函数值y=a+b+c为最大值,
故④正确.
17.或
【详解】
解:向上平移t个单位后,得到的函数解析式为
分析可知:当x=0时,y最大值为t+1,
当x≤2时,x=-2时,y有最小值t-3,
当x>2时,x=t时,y有最小值-t2+t+1,
由题意可知:n是函数值绝对值最大时的值,
(I)当x≤2时,
①t+1≥3-t且,
解得,
②当3-t≥t+1且,
解得
(II)当x>2时,
①t2-t-1≥t+1且
无解;
②t2-t-1<t+1且,
无解,
故答案为:或.
18..
【详解】
解:∵,,,,
∴,,
由平移的性质可知:,
∴四边形的周长为;
要使其周长最小,则应使的值最小;
设抛物线平移了a个单位,当a>0时,抛物线向右平移,当a<0时,抛物线向左平移;
∴,,
将向左平移2个单位得到,则由平移的性质可知:,
将关于x轴的对称点记为点E,则,由轴对称性质可知,,
∴,
当B、E、三点共线时,的值最小,
设直线的解析式为:,
∴,
当时,
∴
∴,
将E点坐标代入解析式可得:,
解得:,
此时,
此时四边形的周长为;
当时,,,,,
此时四边形的周长为:
;
∵,
∴当时,其周长最小,
所以抛物线向右平移了个单位,
所以其解析式为:;
19.y=-x2+2x+3
【详解】
解:∵二次函数经过A(-1,0),B(3,0),C(0,3),
设y=a(x+1)(x-3),
把(0,3)代入得3=-3a,
∴a=-1,
∴该二次函数的解析式是y=-x2+2x+3.
20.(1)抛物线的解析式为;(2)
【分析】
(1)把点A、B的坐标代入求解即可;
(2)由(1)可得,进而可得,然后问题可求解.
【详解】
解:(1)把点和点代入抛物线可得:
,解得:,
∴抛物线的解析式为;
(2)由(1)可得抛物线的解析式为,
∴,
∴,
∴.
21.(1);(2);(3)或.
【详解】
解:(1)把点(﹣2,8)代入y=x2﹣2(m+1)x+3﹣m,
得到,8=4+4(m+1)+3﹣m,
m=﹣1,
∴二次函数的解析式为y=x2+4.
(2)∵对称轴x=﹣=m+1,
又∵x>0时,y随x的增大而增大,
∴m+1≤0,
∴m≤﹣1,
∴m的最大值为﹣1.
(3)∵a=1,
∴抛物线开口向上,
∵二次函数的图象与线段AB只有一个交点(不包括A,B两个端点),
∴满足条件:或,
解得m>0或m<﹣3.
22.(1);(2); (3)以点A、D、P、Q为顶点的四边形能成为矩形点P的坐标为或(1,-4).
【分析】
(1)求两函数交点,直接列等式求解即可;
(2)过点E作轴,交直线l于点F,设,则,则根据计算即可.
(3)令, 求出A、D两点坐标,根据,得到抛物线的对称轴为,设,以点A、D、P、Q为顶点的四边形成为矩形时分为两种情况:第一种,若是矩形的一条边,根据二次函数图像性质,矩形性质,勾股定理列式可求出P点坐标;第二种,若是矩形的一条对角线时,同理可求出点P坐标.
【详解】
解:(1)令,
化解得:,
解得:,
因D点在第四象限,
故时,,
故答案为:,
(2)过点E作轴,交直线l于点F,
设,则,,
,
,
,
,
的面积的最大值为,
的面积最大值为.
,
解得;
(3)令,即,
解得,,,
由(1)知,
,
抛物线的对称轴为,
设,
①若是矩形的一条边,
根据矩形性质以及A、D的坐标可知:,
且,
则 ,
四边形为矩形,,
,
,
即,
,,
,
②若是矩形的一条对角线,
则,
,则,
四边形为矩形,,
,
,
即,, ,
;
综上所述,以点A、D、P、Q为顶点的四边形能成为矩形点P的坐标为
或(1,-4).
23.(1)m=-1;(2)1【详解】
(1)将点(m,?)代入得.
解得m1=m2=-1,
∴m=-1;
(2)∵抛物线的对称轴为直线x=m,
∴直线x=m关于y轴的对称的直线为x=-m,
∵当时,图象G的函数值y先随x的增大而增大,后随x的增大而减小,
∴,
解得1(3)当m≤0,抛物线在x≤2m的部分的函数值y随x的增大而增大.
∴当x=2m时,抛物线在x≤2m的部分有最高点,
∴,
∴最高点的坐标为(2m,m),
∴.
解得(不合题意,舍去)或;
当m>0时,对称轴为,抛物线在x≤2m的部分的最高点坐标为.
∴.
解得或(舍去),
综上所述,当m的值为或时,抛物线在x≤2m的部分图象的最高点到的距离为1;
(4)∵AB⊥轴,
∴代入,
∴AB=2m,BC=AB=m,
∴C(1,),,,
∴E(,),
当抛物线的顶点在矩形的边AC上时,
∴,最大值为,
∴,
∴E(,),即最小值为,
∴最大值与最小值的差为.
当抛物线的顶点在矩形的边CD上时,顶点坐标为(,),
依题意得:,整理得,
解得或,
当时,顶点坐标为(,),
∵,
则抛物线的顶点不在矩形的边CD上,不符合题意,舍去;
当时,顶点坐标为(3,),即最大值为,
E(7,),即最小值为,
最大值与最小值的差为;
当抛物线的顶点在矩形的边DE上时,
则,
解得,不符合题意,
综上,最大值与最小值的差为2或8.
_21?????????è?????(www.21cnjy.com)_
人教版2021年九年级上册数学同步练习卷
22.1二次函数的图像和性质
22.1.4 二次函数y=ax2+bx+k的图像和性质
一、单选题
1.二次函数的最小值为( )
A.-1 B.1 C.2 D.3
2.将抛物线向右平移1个单位,得到抛物线表达式为( )
A. B. C. D.
3.已知二次函数,当时,,则的值是( )
A.3 B.4 C.6 D.7
4.函数的图像可以由函数的图像通过如下平移得到( )
A.向左平移1个单位,再向上平移1个单位
B.向左平移1个单位,再向下平移1个单位
C.向右平移2个单位,再向上平移1个单位
D.向右平移2个单位,再向下平多1个单位
5.若坐标平面上二次函数的图形,经过平移后可与的图形完全叠合,则a、b、c的值可能为下列哪一组?( )
A.,, B.,,
C.,, D.,,
6.已知抛物线上的部分点的横坐标x与纵坐标y的对应值如表:
x … -1 0 1 2 3 …
y … 3 0 -1 m 3 …
以下结论正确的是( )
A.抛物线的开口向下
B.当时,y随x增大而增大
C.方程的根为0和2
D.当时,x的取值范围是
7.二次函数的部分图象如图所示,对称轴为,且经过点.下列说法:①;②;③;④若,是抛物线上的两点,则;⑤(其中).正确的结论有( )
A.2个 B.3个 C.4个 D.5个
8.已知二次函数y=﹣(x﹣1)2+10,当m≤x≤n,且mn<0时,y的最小值为2m,y的最大值为2n,则的值为( )
A.3 B. C.2 D.
9.定义:,若函数,则该函数的最大值为( )
A.0 B.2 C.3 D.4
10.如图,抛物线交轴分别于点,,交轴正半轴于点,抛物线顶点为.下列结论:①;②;③当时,;④当是等腰直角三角形时,;⑤点是抛物线对称轴上的一点,若,则周长的最小值为.其中,正确的个数为( )
A.2个 B.3个 C.4个 D.5个
11.已知二次函数与x轴交于A,B两点,与y轴交于点C.下列说法正确的是( )
①线段的长度为;②抛物线的对称轴为直线;③P是此抛物线的对称轴上的一个动点,当P点坐标为时,的值最大;④若M是x轴上的一个动点,N是此抛物线上的一个动点,如果以A,C,M,N为顶点的四边形是平行四边形,满足条件的M点有4个.
A.①② B.①②③ C.①②④ D.③④
12.如图,A(0,1),B(1,5),曲线BC是双曲线的一部分.曲线AB与BC组成图形G .由点C开始不断重复图形G形成一线“波浪线”.若点P(2020,m) ,Q( x,n )在该“波浪线”上,则m的值为 ,n的最大值为 ( )
A.m = 1,n = 1 B.m = 5,n = 1 C.m = 1,n = 5 D.m = 1,n = 4
二、填空题
13.二次函数的图象开口方向是_______(填“向上”或“向下”).
14.已知函数的部分图像如图所示,那么当x________时,y随x的增大而增大.
15.某校建一个新球场到了最后画线阶段,已知甲在乙的正北50米处沿正东方向以3米/秒的速度画线,同时乙沿正北方向以1米/秒的速度画线,经过___________秒后两人的距离最短.
16.已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象如图所示,下面四个结论,①abc<0;②a+c<b;③2a+b=1;④a+b≥m(am+b),其中全部正确的是______
17.对某一个函数给出如下定义:若存在实数,对于任意的函数值,都满足,则称这个函数是有界函数,在所有满足条件的中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.将函数的图象向上平移个单位,得到的函数的边界值满足是时,则的取值范围是______.
18.如图,已知点,,两点,在抛物线上,向左或向右平移抛物线后,,的对应点分别为,,当四边形的周长最小时,抛物线的解析式为__________.
三、解答题
19.已知二次函数经过求二次函数的表达式.
20.如图,抛物线与轴交于点和点,与轴交于点,连接,与抛物线的对称轴交于点,顶点为点.
(1)求抛物线的解析式;
(2)求的面积.
21.设二次函数y=x2﹣2(m+1)x+3﹣m,其中m是实数.
(1)若函数的图象经过点(﹣2,8),求此函数的表达式;
(2)若x>0时,y随x的增大而增大,求m的最大值.
(3)已知A(﹣1,3),B(2,3),若该二次函数的图象与线段AB只有一个交点(不包括A,B两个端点),求m的取值范围.
22.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B的左侧),经过点A的直线与y轴负半轴交于点C,与抛物线交于另一点D.
(1)则点D的坐标为_______(用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若面积的最大值为,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A、D、P、Q为顶点的四边形成为矩形时,求出点P的坐标.
23.在平面直角坐标系中,抛物线(m为常数).
(1)当点在该抛物线上时,求m的值.
(2)将抛物线在的部分图象沿y轴翻折得到新图象记为G,当时,图象G的函数值y先随x的增大而增大,后随x的增大而减小,求m的取值范围.
(3)当该抛物线在的部分图象的最高点到的距离为1时,求m的值.
(4)当时,过点作垂直于x轴的直线交该抛物线于点B,在AB延长上取一点C,使,将线段AB绕点A顺时针旋转得到线段AE,以AC、AE为邻边作矩形ACDE,当该抛物线的顶点在矩形的边上时,直接写出该抛物线在该矩形内部(包含边界)图象所对应的函数的最大值与最小值的差.
参考答案
1.C
【详解】
解:当时,二次函数有最小值,
且最小值为:,
2.C
【详解】
解:二次函数y=2x2的图象向右平移1个单位,
得:y=2(x-1)2.
3.C
【详解】
∵
∴该函数的对称轴是直线x=3,函数图象开口向上,
当x=3时取得最小值-1,
又∵时,
当x=0时,y=8,当x=6时,y=8,
∴m=6
4.C
【详解】
函数的图像可以由函数的图像通过右平移2个单位,再向上平移1个单位.
5.A
【详解】
解:二次函数的图形,经过平移后可与的图形完全叠合,
.
故选:A.
6.C
利用表中数据求出抛物线的解析式,根据解析式依次进行判断.
【详解】
解:将代入抛物线的解析式得;
,
解得:,
所以抛物线的解析式为:,
A、,抛物线开口向上,故选项错误,不符合题;
B、抛物线的对称轴为直线,在时,y随x增大而增大,故选项错误,不符合题意;
C、方程的根为0和2,故选项正确,符合题意;
D、当时,x的取值范围是或,故选项错误,不符合题意;
7.B
【详解】
解:抛物线的开口向下,与轴的交点位于轴正半轴,
,
抛物线的对称轴为,
,
,则结论①正确;
将点代入二次函数的解析式得:,则结论③错误;
将代入得:,则结论②正确;
抛物线的对称轴为,
和时的函数值相等,即都为,
又当时,随的增大而减小,且,
,则结论④错误;
由函数图象可知,当时,取得最大值,最大值为,
,
,
即,结论⑤正确;
综上,正确的结论有①②⑤,共3个,
8.C
【详解】
解:二次函数y=﹣(x﹣1)2+10的大致图象如下:
.
∵mn<0时,y的最小值为2m,y的最大值为2n,
∴m<0,n>0,
①当n<1时,x=m时,y取最小值,即2m=﹣(m﹣1)2+10,
解得:m=﹣3.
当x=n时,y取最大值,即2n=﹣(n﹣1)2+10,
解得:n=3或n=﹣3(均不合题意,舍去);
②当n≥1时,当x=m时,y取最小值,即2m=﹣(m﹣1)2+10,
解得:m=﹣3.
当x=1时,y取最大值,即2n=﹣(1﹣1)2+10,
解得:n=5,
或x=n时,y取最小值,x=1时,y取最大值,
2m=﹣(n﹣1)2+10,n=5,
∴m=﹣3,
所以m+n=﹣3+5=2.
9.C
【详解】
令,
当时,即时,,
令 ,则w与x轴的交点坐标为(2,0),(-1,0),
∴当时,,
∴(),
∵y随x的增大而增大,
∴当x=2时,;
当时,即时,,
令 ,则w与x轴的交点坐标为(2,0),(-1,0),
∴当时,或,
∴(或),
∵的对称轴为x=1,
∴当时,y随x的增大而减小,
∵当x=2时,=3,
∴当时,y<3;
当,y随x的增大而增大,
∴当x=-1时,=0;
∴当时,y<0;
综上,的最大值为3.
10.D
【详解】
解:把点,,代入得到,
消去得到,故①,②正确,
∵抛物线的对称轴,开口向下,
∴时,有最大值,最大值,
∵,
∴,
∴,故③正确,
当是等腰直角三角形时,,
可以假设抛物线的解析式为,把(1,0)代入得到,故④正确,
如图,连接交抛物线的对称轴于,连接,此时的周长最小,
最小值,
∵,,
∴△PBD周长最小值为,故⑤正确.
11.C
【详解】
解:在中,
令x=0,则y=2,
令y=0,则,
解得x=或2,
∴A(,0),C(0,2),
∴AC=,①正确;
∵,
∴抛物线的对称轴为直线,②正确;
延长AC,与对称轴交于点P,此时的值最大,
∵A(,0),C(0,2),设直线AC的表达式为:y=mx+n,
则,解得:,
∴直线AC的表达式为y=4x+2,
令,则y=5,
∴当点P的坐标为(,5)时,的值最大,③错误;
如图,若以A,C,M,N为顶点的四边形是平行四边形,
当AC为边时,有ACM1N1,ACM2N2,ACM3N3,共3个平行四边形,
当AC为对角线时,有AMCN1,共1个平行四边形,
∴符合条件的点M有4个,④正确,
故选C.
12.C
【详解】
解:∵点B(1,5)在双曲线的图象上,
∴k=5,
∵A(0,1),曲线AB与BC组成图形G .由点C开始不断重复图形G形成一线“波浪线”.
∴C的纵坐标为1
∵点C在的图象上,点C的纵坐标为1,
∴点C的横坐标是5,
∴点C的坐标为(5,1),
∵2020÷5=404,
∴P(2020,m)中m=1
∵点Q(x,n)在该“波浪线”上,
∴n的最大值是5.
综上所述,m = 1,n = 5.
13.向上
【详解】
解:∵二次函数,a=1>0,
∴二次函数的图象开口方向向上,
故答案是:向上.
14.<1
【详解】
解:根据图象得:
函数图像开口向下,对称轴为直线x=1,
∴当x<1时,y随x的增大而增大,
15.5
【详解】
解:设t秒时甲乙两者间的距离最短,
依题意得AD=3tm,BA=50m,BC=tm,AC=(50-t)m,
在Rt△ADC中
由勾股定理得CD=,
,
,
,
当t=5时CD最短.
16.①②④.
【详解】
解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴a,b异号,b>0,
∵抛物线与y轴交点在y轴正半轴,
∴c>0,
∴abc<0,
故①正确;
由图象得当x=-1时,y=a-b+c<0,
∴a+c<b,
故②正确;
∵图象对称轴为直线x==1,
∴﹣b=2a,即2a+b=0,
故③错误;
由a+b≥m(am+b)得a+b+c≥am2+bm+c,
∵x=1时函数值y=a+b+c为最大值,
故④正确.
17.或
【详解】
解:向上平移t个单位后,得到的函数解析式为
分析可知:当x=0时,y最大值为t+1,
当x≤2时,x=-2时,y有最小值t-3,
当x>2时,x=t时,y有最小值-t2+t+1,
由题意可知:n是函数值绝对值最大时的值,
(I)当x≤2时,
①t+1≥3-t且,
解得,
②当3-t≥t+1且,
解得
(II)当x>2时,
①t2-t-1≥t+1且
无解;
②t2-t-1<t+1且,
无解,
故答案为:或.
18..
【详解】
解:∵,,,,
∴,,
由平移的性质可知:,
∴四边形的周长为;
要使其周长最小,则应使的值最小;
设抛物线平移了a个单位,当a>0时,抛物线向右平移,当a<0时,抛物线向左平移;
∴,,
将向左平移2个单位得到,则由平移的性质可知:,
将关于x轴的对称点记为点E,则,由轴对称性质可知,,
∴,
当B、E、三点共线时,的值最小,
设直线的解析式为:,
∴,
当时,
∴
∴,
将E点坐标代入解析式可得:,
解得:,
此时,
此时四边形的周长为;
当时,,,,,
此时四边形的周长为:
;
∵,
∴当时,其周长最小,
所以抛物线向右平移了个单位,
所以其解析式为:;
19.y=-x2+2x+3
【详解】
解:∵二次函数经过A(-1,0),B(3,0),C(0,3),
设y=a(x+1)(x-3),
把(0,3)代入得3=-3a,
∴a=-1,
∴该二次函数的解析式是y=-x2+2x+3.
20.(1)抛物线的解析式为;(2)
【分析】
(1)把点A、B的坐标代入求解即可;
(2)由(1)可得,进而可得,然后问题可求解.
【详解】
解:(1)把点和点代入抛物线可得:
,解得:,
∴抛物线的解析式为;
(2)由(1)可得抛物线的解析式为,
∴,
∴,
∴.
21.(1);(2);(3)或.
【详解】
解:(1)把点(﹣2,8)代入y=x2﹣2(m+1)x+3﹣m,
得到,8=4+4(m+1)+3﹣m,
m=﹣1,
∴二次函数的解析式为y=x2+4.
(2)∵对称轴x=﹣=m+1,
又∵x>0时,y随x的增大而增大,
∴m+1≤0,
∴m≤﹣1,
∴m的最大值为﹣1.
(3)∵a=1,
∴抛物线开口向上,
∵二次函数的图象与线段AB只有一个交点(不包括A,B两个端点),
∴满足条件:或,
解得m>0或m<﹣3.
22.(1);(2); (3)以点A、D、P、Q为顶点的四边形能成为矩形点P的坐标为或(1,-4).
【分析】
(1)求两函数交点,直接列等式求解即可;
(2)过点E作轴,交直线l于点F,设,则,则根据计算即可.
(3)令, 求出A、D两点坐标,根据,得到抛物线的对称轴为,设,以点A、D、P、Q为顶点的四边形成为矩形时分为两种情况:第一种,若是矩形的一条边,根据二次函数图像性质,矩形性质,勾股定理列式可求出P点坐标;第二种,若是矩形的一条对角线时,同理可求出点P坐标.
【详解】
解:(1)令,
化解得:,
解得:,
因D点在第四象限,
故时,,
故答案为:,
(2)过点E作轴,交直线l于点F,
设,则,,
,
,
,
,
的面积的最大值为,
的面积最大值为.
,
解得;
(3)令,即,
解得,,,
由(1)知,
,
抛物线的对称轴为,
设,
①若是矩形的一条边,
根据矩形性质以及A、D的坐标可知:,
且,
则 ,
四边形为矩形,,
,
,
即,
,,
,
②若是矩形的一条对角线,
则,
,则,
四边形为矩形,,
,
,
即,, ,
;
综上所述,以点A、D、P、Q为顶点的四边形能成为矩形点P的坐标为
或(1,-4).
23.(1)m=-1;(2)1
(1)将点(m,?)代入得.
解得m1=m2=-1,
∴m=-1;
(2)∵抛物线的对称轴为直线x=m,
∴直线x=m关于y轴的对称的直线为x=-m,
∵当时,图象G的函数值y先随x的增大而增大,后随x的增大而减小,
∴,
解得1
∴当x=2m时,抛物线在x≤2m的部分有最高点,
∴,
∴最高点的坐标为(2m,m),
∴.
解得(不合题意,舍去)或;
当m>0时,对称轴为,抛物线在x≤2m的部分的最高点坐标为.
∴.
解得或(舍去),
综上所述,当m的值为或时,抛物线在x≤2m的部分图象的最高点到的距离为1;
(4)∵AB⊥轴,
∴代入,
∴AB=2m,BC=AB=m,
∴C(1,),,,
∴E(,),
当抛物线的顶点在矩形的边AC上时,
∴,最大值为,
∴,
∴E(,),即最小值为,
∴最大值与最小值的差为.
当抛物线的顶点在矩形的边CD上时,顶点坐标为(,),
依题意得:,整理得,
解得或,
当时,顶点坐标为(,),
∵,
则抛物线的顶点不在矩形的边CD上,不符合题意,舍去;
当时,顶点坐标为(3,),即最大值为,
E(7,),即最小值为,
最大值与最小值的差为;
当抛物线的顶点在矩形的边DE上时,
则,
解得,不符合题意,
综上,最大值与最小值的差为2或8.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
