探索三角形全等的条件

(共28张PPT)
学习目标
1.经历探索三角形全等条件的过程，并体 会利用操作、归纳获得数学结论的过 程。
2.掌握判定三角形全等的条件，能够运用 SSS定理判定两个三角形全等，学会通过证明三角形全等，从而证明两角、两线段相等。
3.在探索三角形全等条件及其运用的过程中，培养推理能力和逻辑思维能力。
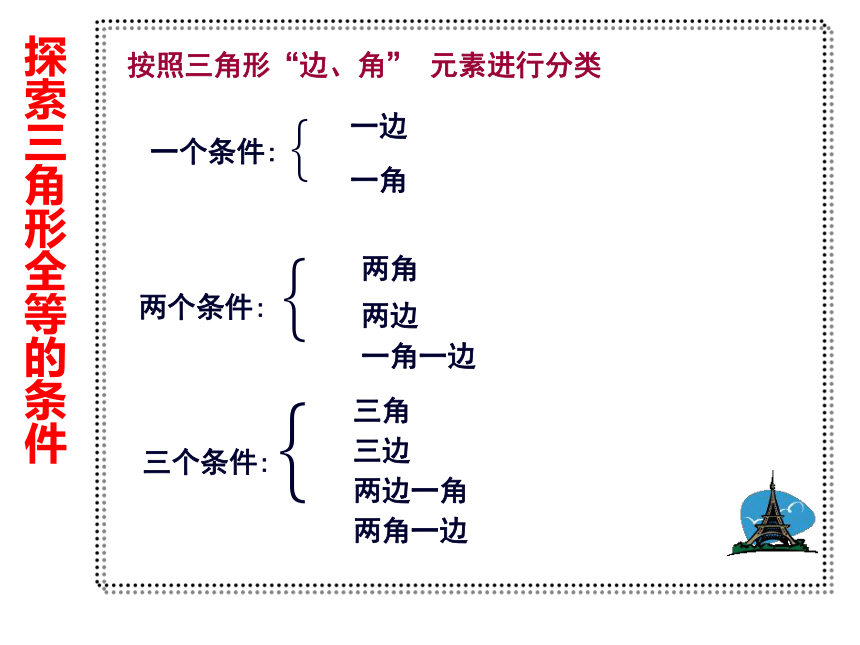
按照三角形“边、角” 元素进行分类
两个条件:
一角一边
两边
两角
{
一个条件:
{
一边
一角
三个条件:
两角一边
两边一角
三边
三角
{
探索三角形全等的条件
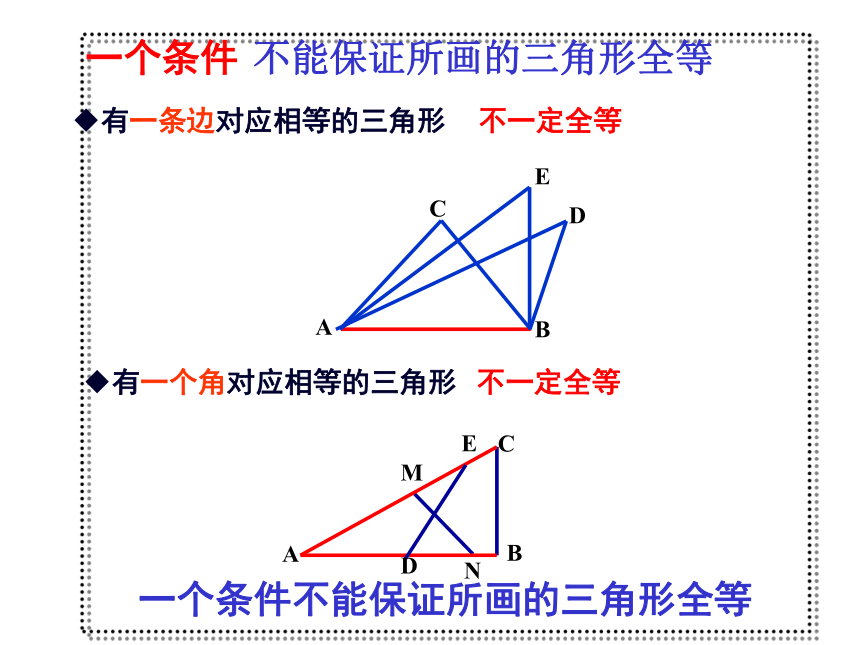
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
一个条件不能保证所画的三角形全等
A
B
C
D
E
A
B
C
D
E
M
N
不能保证所画的三角形全等
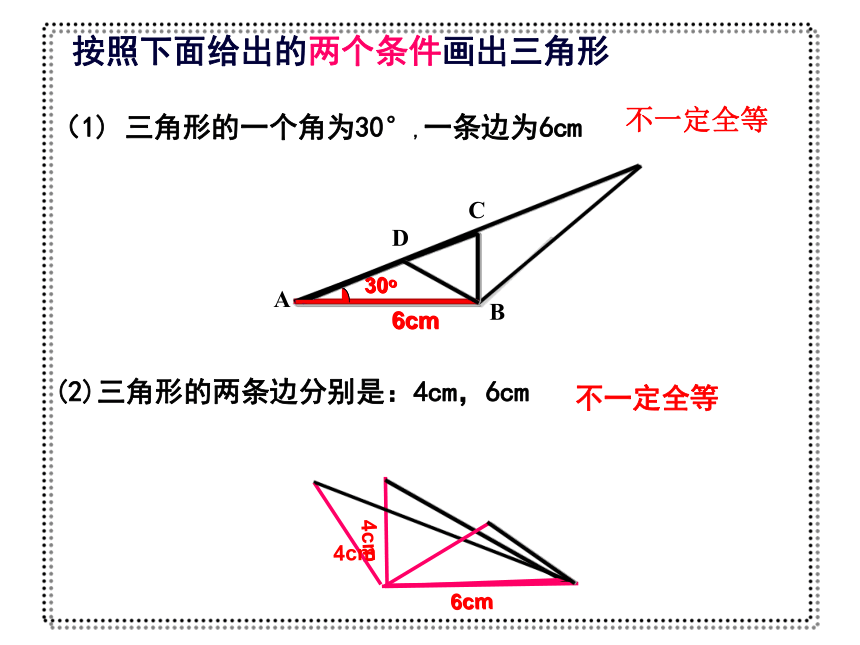
按照下面给出的两个条件画出三角形
（1) 三角形的一个角为30°,一条边为6cm
30o
6cm
(2)三角形的两条边分别是：4cm，6cm
4cm
6cm
4cm
6cm
不一定全等
不一定全等
30o
6cm
B
A
C
30o
6cm
D
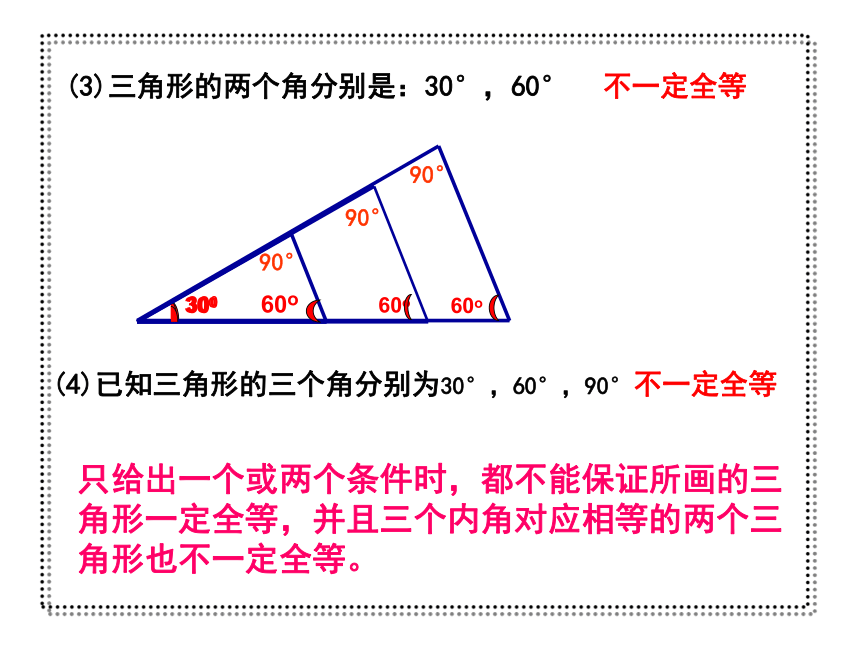
(3)三角形的两个角分别是：30°，60°
(4)已知三角形的三个角分别为30°，60°，90°
300
60o
300
60o
60o
300
不一定全等
不一定全等
只给出一个或两个条件时，都不能保证所画的三角形一定全等，并且三个内角对应相等的两个三角形也不一定全等。
90°
90°
90°
已知三角形三条边分别是4cm，5cm，7cm，画出这个三角形，把所画的三角形分别剪下来，并与同伴比一比，发现什么？
探索新知
已知三角形三条边分别是4cm，5cm，7cm，画出这个三角形，把所画的三角形分别剪下来，并与同伴比一比，发现什么？
探索新知
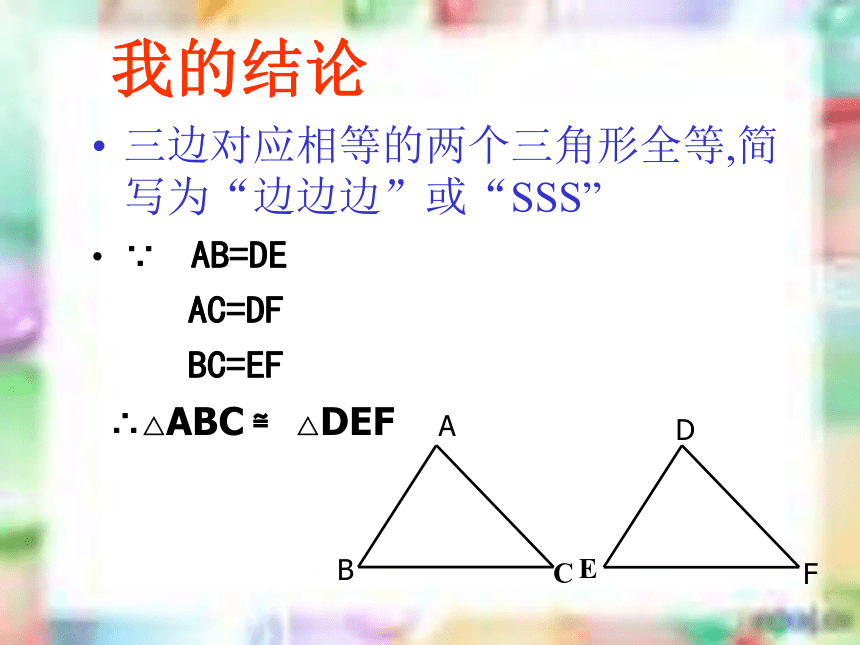
我的结论
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”
∵ AB=DE
AC=DF
BC=EF
∴△ABC ≌ △DEF
A
B
C
D
F
E
如图, △ABC 是刚架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD
A
C
D
B
证明:
在△ABD 和△ACD中
∵ AB = AC
∴ △ABD ≌ △ACD
(已知)
(公共边)
(已知)
AD = AD
DB = DC
( SSS )
学以致用
如图, △ABC 是刚架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: AD ⊥ BC
A
C
D
1
2
B
∴ ∠ 1 =∠ 2
证明:
在△ABD 和△ACD中
∵ AB = AC
AD = AD
DB = DC
∴ △ABD ≌ △ACD ( SSS )
(全等三角形的对应角相等)
∴ ∠ 1 = ∠ BDC = 90 °
1
2
∴ AD ⊥ BC
(平角定义)
(垂直定义)
学以致用
例题2
已知: 如图,AB = DC ,AD = BC .
求证: ∠ A =∠ C
证明:
在△BAD 和△DCB中
∵ AB = CD
AD = CB
BD = DB
∴ △BAD ≌ △DCB( SSS )
∴ ∠ A =∠ C
(已知)
(已知)
(公共边)
(全等三角形的对应角相等)
A
B
C
D
连结 BD
已知: 如图,点B、E、C、F在同一直线上 ,
AB = DE ,AC = DF ,BE = CF .
求证: ∠ A =∠ D
C
A
B
D
F
E
证明:
∴ △ABC ≌ △DEF ( SSS )
在△ABC 和△DEF中
∵ AB = DE
AC = DF
BC = EF
∴ ∠ A =∠ D
(全等三角形的对应角相等)
∵ BE = CF
∴ BC = EF
∴ BE+EC = CF+CE
例题3
练习1
如图已知: A、C、D、F四点在同一直线上，
AB = DE ,BC = EF ,AC = DF.
求证: AB ∥ DE
A
B
C
D
E
F
分析:
AB ∥ DE
∠ A =∠ D
△ABC ≌ △DEF ( SSS )
AB = DE BC = EF AC = DF
A
B
C
D
E
F
证明:
在△ABC 和△DEF中
∵ AB = DE
BC = EF
AC = DF
∴ △ABC ≌ △DEF ( SSS )
∴ AB ∥ DE
∴ ∠ A =∠ D
甲
(已知)
(已知)
(已知)
(全等三角形对应角相等)
(内错角相等两直线平行)
如图已知: A、C、D、F四点在同一直线上,
AB = DE ,BC = EF ,AC = DF.
求证: AB ∥ DE
练习 2
A
B
C
D
E
F
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
甲
练习 2
A
B
C
D
E
F
练习2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
A
B
C
D
E
F
练习 2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
A
B
C
D
E
F
练习 2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
A
B
C
D
E
F
乙
证明:
在△ABC 和△DEF中
AB = DE
BC = EF
AC = DF
∴ △ABC ≌ △DEF ( SSS )
∴ AB ∥ DE
∴ ∠ A =∠ D
(已知)
(已知)
(已知)
(全等三角形对应角相等)
(内错角相等两直线平行)
练习 2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
A
B
C
D
E
F
乙
练习 2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
A
B
C
D
E
F
丙
证明:
在△ABC 和△DEF中
AB = DE
BC = EF
AC = DF
∴ △ABC ≌ △DEF ( SSS )
∴ AB ∥ DE
∴ ∠ A =∠ D
(已知)
(已知)
(已知)
(全等三角形对应角相等)
(内错角相等两直线平行)
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
我能行
A
B
C
D
E
F
练习 2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
A
B
C
D
E
F
练习 2
把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化
BC
BC
△DCB
BF=DC
或 BD=FC
A
B
C
D
解： △ABC≌△DCB
理由如下：
AB = CD
AC = BD
=
△ABD ≌ （ ）
S S S
（1）如图，AB=CD，AC=BD，△ABC和△DCB是否全等？ 试说明理由。
（2）如图，D、F是线段BC上的两点，
AB=CE，AF=DE，要使△ABF≌△ECD ，
还需要条件
A
E
B D F C
我能行
1.本课通过作图，动手操作,探索了三角形全等的条件。
2.掌握判定三角形全等的定理，即三边对应相等的两个三角形全等。
3.能够运用SSS定理判定两个三角形全 等，学会可以通过证明三角形全等来证明两角、两线相等。
4.学会通过连线或加、减公共边，寻找题 目中隐含的条件。
5.会根据已知条件进行有条理的思考，逻辑思维能力有所提高。
我的收获
知识的升华
独立
作业
A. P101　作业题１，２题.
（做在作业本上）
B .一腰和底边对应相等的两个等腰三角形全等吗？请说明理由
谢谢，再见