七年级数学有理数的加法课件
图片预览



文档简介
(共28张PPT)
§1.3.1
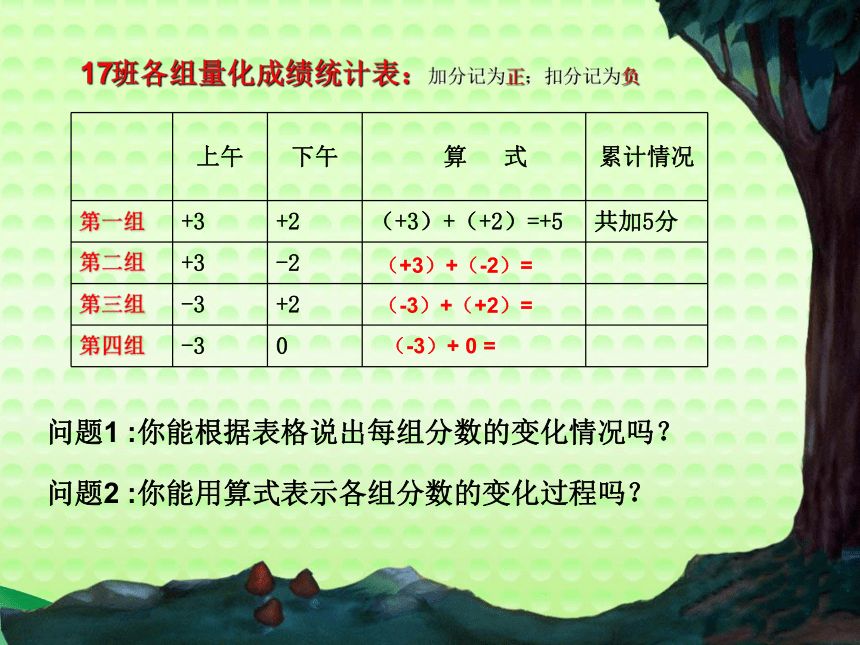
上午 下午 算 式 累计情况
第一组 +3 +2 (+3)+(+2)=+5 共加5分
第二组 +3 -2
第三组 -3 +2
第四组 -3 0
问题1 :你能根据表格说出每组分数的变化情况吗?
问题2 :你能用算式表示各组分数的变化过程吗?
17班各组量化成绩统计表:加分记为正;扣分记为负
(+3)+(-2)=
(-3)+(+2)=
(-3)+ 0 =
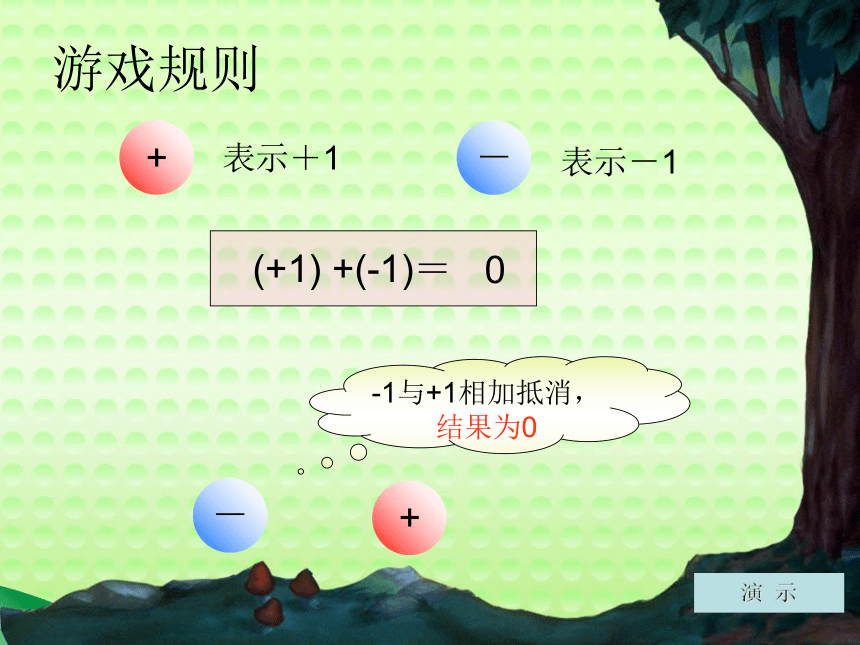
游戏规则
-
+
(+1) +(-1)=
演 示
-1与+1相加抵消,结果为0
-
+
表示+1
表示-1
0
利用游戏规则,如何解释下面算式的结果
(1)、2 +(-5)=
(2)、8 +(-6)=
(3)、(-8) +5=
(4)、5 +3=
(5)、(-2) +(-3)=
利用游戏规则,如何解释下面算式的结果
(1)、2 +(-5)=
(2)、8 +(-6)=
(3)、(-8) +5=
(4)、5 +3=
(5)、(-2) +(-3)=
你还能用其他方法来解释有理数的加法运算吗?
小组讨论,并用你的方法解释以上五道算式的运算结果.
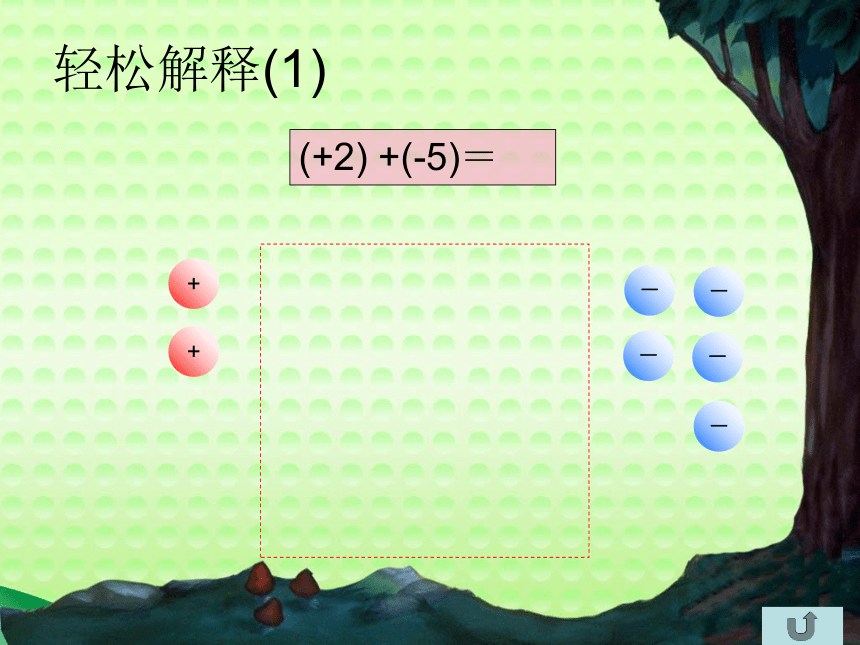
轻松解释(1)
-
+
(+2) +(-5)=
-
-
-
-
+
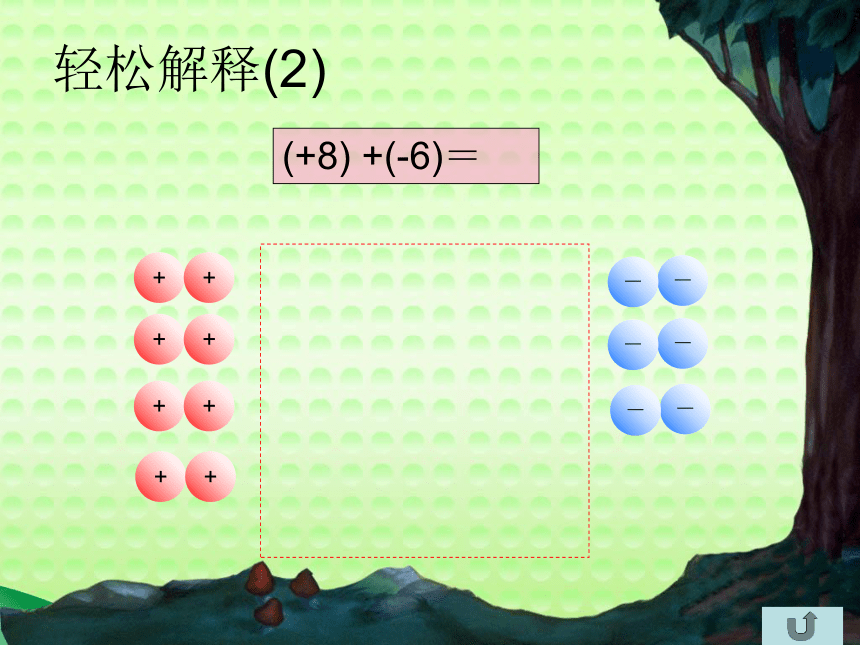
轻松解释(2)
(+8) +(-6)=
+
+
-
-
+
+
+
+
-
-
-
-
+
+
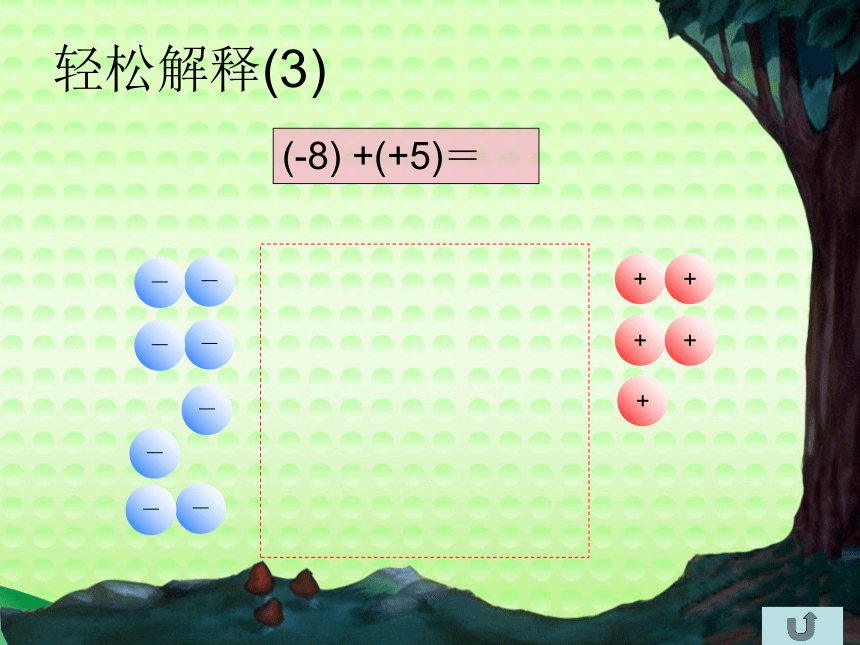
轻松解释(3)
(-8) +(+5)=
+
+
-
-
+
+
+
-
-
-
-
-
-
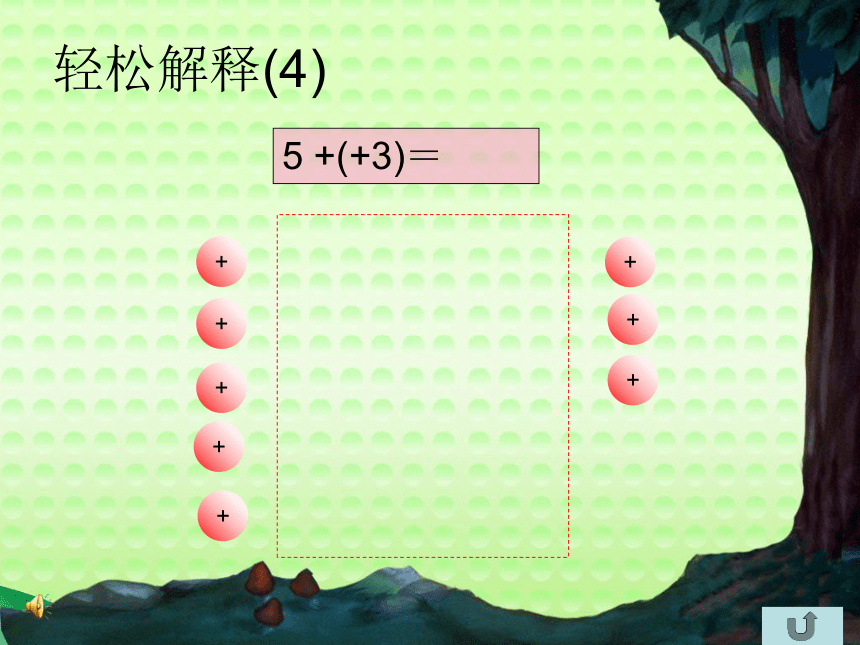
轻松解释(4)
5 +(+3)=
+
+
+
+
+
+
+
+
轻松解释(5)
(-2) +(-3)=
-
-
-
-
-
0
1
2
3
4
-1
-2
-3
若规定向右为正,则向左为负
向右运动3米记为: +3米
向左运动1米记为:
-1米
0
3
5
(+3)
+(+2)
=+5
先向右运动3米
又向右运动2米
则两次运动后从起点向___运动了___米
右
5
0
-3
-5
(-3)
+(-2)
=-5
先向左运动3米
又向左运动2米
则两次运动后从起点向___运动了___米
左
5
0
3
1
(+3)
+(-2)
=+1
先向右运动3米
又向左运动2米
则两次运动后从起点向___运动了___米
右
1
0
-3
-1
(-3)
+(+2)
=-1
先向左运动3米
又向右运动2米
则两次运动后从起点向___运动了___米
左
1
0
3
(+3)
+(-3)
=0
先向右运动3米
又向左运动3米
则两次运动后____________
回到起点
0
-3
0
+(-3)
=-3
先运动0米
又向左运动3米
则两次运动后从起点向___运动了___米
左
3
(1) (+3)+(+2) =+5
观察下列算式:
(4) (-3)+(+2)=-1
怎样来表示是向左还是向右呢?
最终相对原点的距离又是由什么来体现的?
数的符号
绝对值
(2) (-3)+(-2) =-5
(3) (+3)+(-2) =+1
(5) (-3)+(+3) =0
(6) (0)+(-3) =-3
(1) (+3)+(+2) =+5
观察下列算式中各个加数的特征:
(4) (-3)+(+2)=-1
(2) (-3)+(-2) =-5
(3) (+3)+(-2) =+1
(5) (-3)+(+3) =0
(6) (0)+(+3) =+3
在两个有理数相加的过程中“和的符号”怎样确定?
“和的绝对值”怎样确定?
上面6个式子表示了几种不同的有理数相加?
赶快动脑筋,说说自己的想法
有理数的加法
同号两数相加,取与加数相同的符号,并把绝对值相加.
异号两数相加,取与绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得零;一个数同零相加仍得这个数.
加数 加数 和的组成 和
符号 绝对值
-15 5
17 6
-8 18
-8 -6
-10 5
-
+
+
-
-
15-5
17+6
18-8
8+6
10-5
-10
+23
+10
-14
-5
上午 下午 算 式 累计情况
第一组 +3 +2 (+3)+(+2)=+5 共加5分
第二组 +3 -2
第三组 -3 +2
第四组 -3 0
17班各组量化成绩统计表:
(+3)+(-2)=
(-3)+(+2)=
(-3)+ 0 =
有理数加法的运算步骤
再确定和的符号;
后进行绝对值的加减运算
先判断类型 (同号、异号等);
谁是“运算王”
比赛规则:
1. 每次每人抽一张,按两人所抽的牌面数字做加法运算
2.红色牌代表正数,黑色牌代表负数,大小王代表0
3.不仅要算得快,还要说明算理。
4.三分钟内完成次数最多的获胜
请获胜的学生谈获胜的秘诀。
请同学们拿出扑克牌,同桌间进行有理数加法运算的抢答比赛。
回顾与反思:
这节课我们研究了什么数学问题?
在研究这个问题时,我们经历了怎样的过程? 用到了哪些数学思想方法?
通过这个过程,你有什么感受和体会?
生活情境
运算的实例
运算的本质属性
获得运算法则
深化巩固
提炼、抽象
探索、归纳
概括、表达
解释、应用
数学与我们的生活密切相关,我们遇到实际问题时要善于用数学的方法。希望通过今天这节课我们学到的不仅是数学知识,更重要的是学习这些知识的思想和方法。
1.必做题:课本第24页习题1.3第1题
2.选做题:习题1.3第12题
3.思考题:“两个有理数相加,和一定大于其中一个加数”,该说法正确吗?请举例说明。
4.请同学们回家用扑克牌和父母进行有理数加法运算比赛。
作业
§1.3.1
上午 下午 算 式 累计情况
第一组 +3 +2 (+3)+(+2)=+5 共加5分
第二组 +3 -2
第三组 -3 +2
第四组 -3 0
问题1 :你能根据表格说出每组分数的变化情况吗?
问题2 :你能用算式表示各组分数的变化过程吗?
17班各组量化成绩统计表:加分记为正;扣分记为负
(+3)+(-2)=
(-3)+(+2)=
(-3)+ 0 =
游戏规则
-
+
(+1) +(-1)=
演 示
-1与+1相加抵消,结果为0
-
+
表示+1
表示-1
0
利用游戏规则,如何解释下面算式的结果
(1)、2 +(-5)=
(2)、8 +(-6)=
(3)、(-8) +5=
(4)、5 +3=
(5)、(-2) +(-3)=
利用游戏规则,如何解释下面算式的结果
(1)、2 +(-5)=
(2)、8 +(-6)=
(3)、(-8) +5=
(4)、5 +3=
(5)、(-2) +(-3)=
你还能用其他方法来解释有理数的加法运算吗?
小组讨论,并用你的方法解释以上五道算式的运算结果.
轻松解释(1)
-
+
(+2) +(-5)=
-
-
-
-
+
轻松解释(2)
(+8) +(-6)=
+
+
-
-
+
+
+
+
-
-
-
-
+
+
轻松解释(3)
(-8) +(+5)=
+
+
-
-
+
+
+
-
-
-
-
-
-
轻松解释(4)
5 +(+3)=
+
+
+
+
+
+
+
+
轻松解释(5)
(-2) +(-3)=
-
-
-
-
-
0
1
2
3
4
-1
-2
-3
若规定向右为正,则向左为负
向右运动3米记为: +3米
向左运动1米记为:
-1米
0
3
5
(+3)
+(+2)
=+5
先向右运动3米
又向右运动2米
则两次运动后从起点向___运动了___米
右
5
0
-3
-5
(-3)
+(-2)
=-5
先向左运动3米
又向左运动2米
则两次运动后从起点向___运动了___米
左
5
0
3
1
(+3)
+(-2)
=+1
先向右运动3米
又向左运动2米
则两次运动后从起点向___运动了___米
右
1
0
-3
-1
(-3)
+(+2)
=-1
先向左运动3米
又向右运动2米
则两次运动后从起点向___运动了___米
左
1
0
3
(+3)
+(-3)
=0
先向右运动3米
又向左运动3米
则两次运动后____________
回到起点
0
-3
0
+(-3)
=-3
先运动0米
又向左运动3米
则两次运动后从起点向___运动了___米
左
3
(1) (+3)+(+2) =+5
观察下列算式:
(4) (-3)+(+2)=-1
怎样来表示是向左还是向右呢?
最终相对原点的距离又是由什么来体现的?
数的符号
绝对值
(2) (-3)+(-2) =-5
(3) (+3)+(-2) =+1
(5) (-3)+(+3) =0
(6) (0)+(-3) =-3
(1) (+3)+(+2) =+5
观察下列算式中各个加数的特征:
(4) (-3)+(+2)=-1
(2) (-3)+(-2) =-5
(3) (+3)+(-2) =+1
(5) (-3)+(+3) =0
(6) (0)+(+3) =+3
在两个有理数相加的过程中“和的符号”怎样确定?
“和的绝对值”怎样确定?
上面6个式子表示了几种不同的有理数相加?
赶快动脑筋,说说自己的想法
有理数的加法
同号两数相加,取与加数相同的符号,并把绝对值相加.
异号两数相加,取与绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得零;一个数同零相加仍得这个数.
加数 加数 和的组成 和
符号 绝对值
-15 5
17 6
-8 18
-8 -6
-10 5
-
+
+
-
-
15-5
17+6
18-8
8+6
10-5
-10
+23
+10
-14
-5
上午 下午 算 式 累计情况
第一组 +3 +2 (+3)+(+2)=+5 共加5分
第二组 +3 -2
第三组 -3 +2
第四组 -3 0
17班各组量化成绩统计表:
(+3)+(-2)=
(-3)+(+2)=
(-3)+ 0 =
有理数加法的运算步骤
再确定和的符号;
后进行绝对值的加减运算
先判断类型 (同号、异号等);
谁是“运算王”
比赛规则:
1. 每次每人抽一张,按两人所抽的牌面数字做加法运算
2.红色牌代表正数,黑色牌代表负数,大小王代表0
3.不仅要算得快,还要说明算理。
4.三分钟内完成次数最多的获胜
请获胜的学生谈获胜的秘诀。
请同学们拿出扑克牌,同桌间进行有理数加法运算的抢答比赛。
回顾与反思:
这节课我们研究了什么数学问题?
在研究这个问题时,我们经历了怎样的过程? 用到了哪些数学思想方法?
通过这个过程,你有什么感受和体会?
生活情境
运算的实例
运算的本质属性
获得运算法则
深化巩固
提炼、抽象
探索、归纳
概括、表达
解释、应用
数学与我们的生活密切相关,我们遇到实际问题时要善于用数学的方法。希望通过今天这节课我们学到的不仅是数学知识,更重要的是学习这些知识的思想和方法。
1.必做题:课本第24页习题1.3第1题
2.选做题:习题1.3第12题
3.思考题:“两个有理数相加,和一定大于其中一个加数”,该说法正确吗?请举例说明。
4.请同学们回家用扑克牌和父母进行有理数加法运算比赛。
作业
