浙江省宁波万里国际学校2011-2012学年高二上学期期中考试数学试题
文档属性
| 名称 | 浙江省宁波万里国际学校2011-2012学年高二上学期期中考试数学试题 | 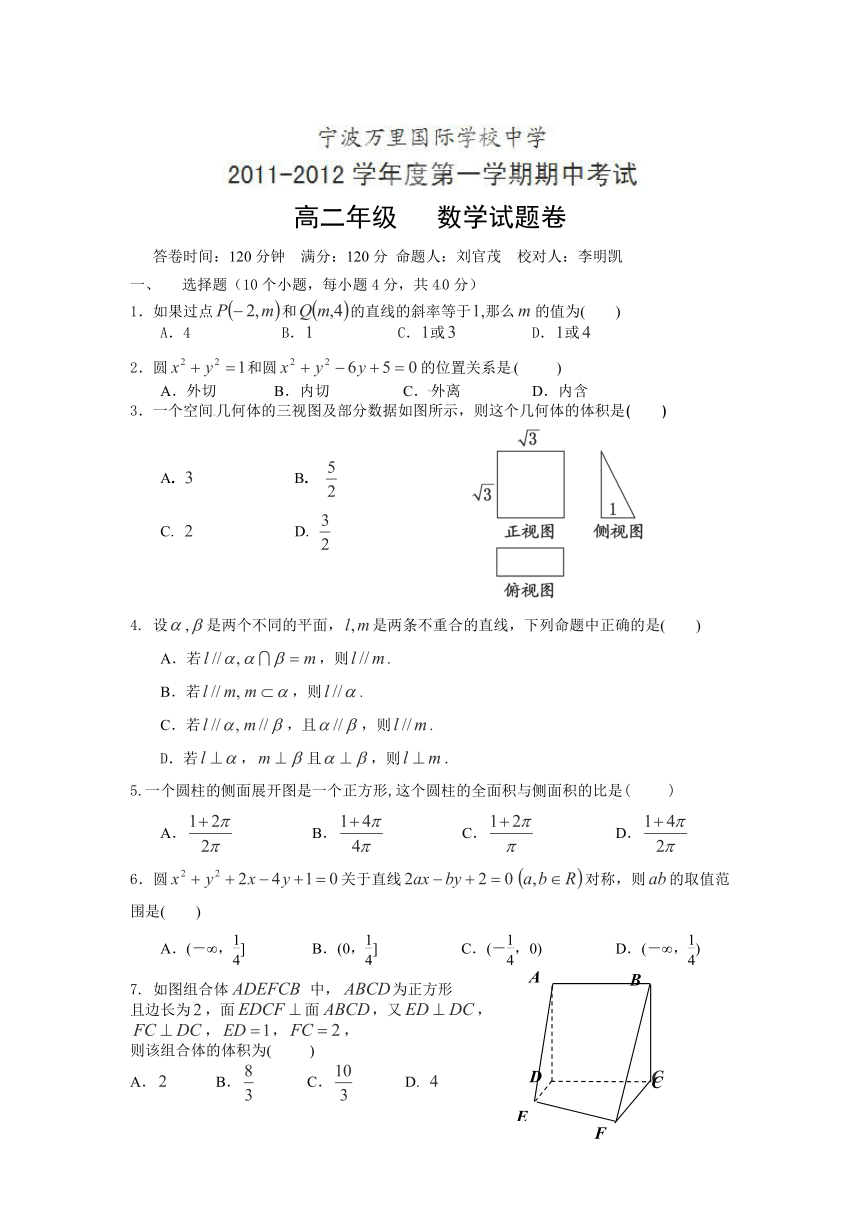 | |
| 格式 | zip | ||
| 文件大小 | 249.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-07 20:41:30 | ||
图片预览


文档简介
高二年级 数学试题卷
答卷时间:120分钟 满分:120分 命题人:刘官茂 校对人:李明凯
选择题(10个小题,每小题4分,共40分)
1.如果过点和的直线的斜率等于,那么的值为( )
A.4 B. C.或 D.或
2.圆和圆的位置关系是( )
A.外切 B.内切 C.外离 D.内含
3.一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )
A. B.
C. D.
4. 设,是两个不同的平面,是两条不重合的直线,下列命题中正确的是( )
A.若,则.
B.若,则.
C.若,且,则.
D.若,且,则.
5.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A. B. C. D.
6.圆关于直线对称,则的取值范围是( )
A.(-∞,] B.(0,] C.(-,0) D.(-∞,)
7. 如图组合体 中,为正方形
且边长为,面面,又,
,,,
则该组合体的体积为( )
A. B. C. D.
8.在长方体中,.
若分别为线段,的中点,则直线与
平面所成角的余弦值为( )
A. B. C. D.
9.由直线上的点向圆引切线,则切线长的最小值为 ( )
A. B. C. D.
10.过点作圆的弦,其中弦长为整数的共有( )
A.条 B.条 C.条 D.条
二、填空题(7个小题,每小题4分,共28分)
11.已知直线过点且直线的倾斜角为则直线的方程为 ________________.
12.与圆: 关于直线: 对称的圆的方程为_________.
13.考察下列三个命题,在“________”都缺少同一个条件,补上这个条件使其构成真命题(其中为不同直线,为不同平面),则此条件为______________.
① ; ② ; ③
14.如下图,在正方体中,
是中点,是的中点,则直线
与所成角的大小为_______.
15.已知直线和直线平行,则________.
16.圆上有四点到直线的距离为,则的取值范围为______________.
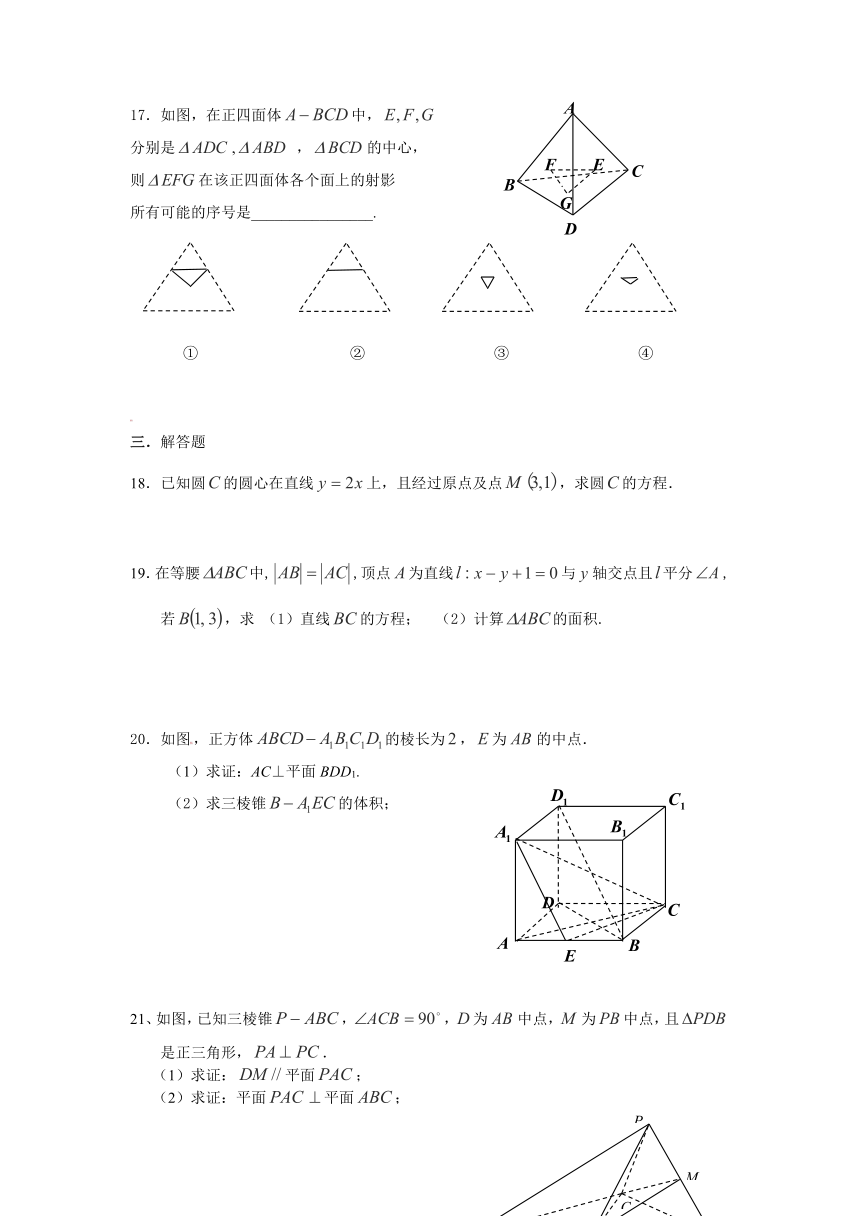
17.如图,在正四面体中,
分别是, ,的中心,
则在该正四面体各个面上的射影
所有可能的序号是________________.
① ② ③ ④
三.解答题
18.已知圆的圆心在直线上,且经过原点及点,求圆的方程.
19.在等腰中,,顶点为直线与轴交点且平分,
若,求 (1)直线的方程; (2)计算的面积.
20.如图,正方体的棱长为,为的中点.
(1)求证:AC⊥平面BDD1.
(2)求三棱锥的体积;
21、如图,已知三棱锥,,为中点,为中点,且是正三角形,.
(1)求证:平面;
(2)求证:平面平面;
22.已知圆:
(1)平面上有两点,求过点两点的直线被圆截得的弦长;
(2)已知过点的直线平分圆的周长,是直线上的动点,
并且,求的最小值.
(3) 若是轴上的动点,分别切圆于两点.
试问:直线是否恒过定点?如是,求出定点坐标,如不是,说明理由.
宁波万里国际学校中学
2011-2012学年度第一学期期中考试
[高二]年级 参考答案
选择题:
填空题:
11、 12、
13、 14、
15、 16、
17、③④
三、解答题:
18、解: 根据题意,设圆的方程为:
因为圆经过原点和,故此有:
…… ①
…… ②
两式联立,解得: ,
所以,所求的园的方程为:
19、解:根据题意知,又因为,平分,
所以两点关于直线对称,设
利用方程组我们容易得到
进而直线方程为:
(2)由点到直线距离公式得到到直线的距离为,又
所以,有
20.如图,正方体的棱长为,为的中点.
(1)求证:AC⊥平面BDD1.
(2)求三棱锥的体积;
略;
21、如图,已知三棱锥,,为中点,为中点,且是正三角形,.
(1)求证:平面;
(2)求证:平面平面;
略;
关键点就是证明
22.已知圆:
(1)平面上有两点,求过点两点的直线被圆截得的弦长;
(2)已知过点的直线平分圆的周长,是直线上的动点,
并且,求的最小值.
(3) 若是轴上的动点,分别切圆于两点.
试问:直线是否恒过定点?如是,求出定点坐标,如不是,说明理由.
解:(1)因为直线经过两点,从而直线的方程为
进而令中的得或
故此直线被圆截得的弦长为. …… 3分
(2) 因为圆的圆心为, 又直线过点,
所以直线的方程是:
而在直线上, 所以有: 也即有
, 进而有:
故当,即时,又,
从而时取得最小值
即直线恒过定点……………12分
D
P
M
C
B
A
座位号
D
P
M
C
B
A
答卷时间:120分钟 满分:120分 命题人:刘官茂 校对人:李明凯
选择题(10个小题,每小题4分,共40分)
1.如果过点和的直线的斜率等于,那么的值为( )
A.4 B. C.或 D.或
2.圆和圆的位置关系是( )
A.外切 B.内切 C.外离 D.内含
3.一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )
A. B.
C. D.
4. 设,是两个不同的平面,是两条不重合的直线,下列命题中正确的是( )
A.若,则.
B.若,则.
C.若,且,则.
D.若,且,则.
5.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A. B. C. D.
6.圆关于直线对称,则的取值范围是( )
A.(-∞,] B.(0,] C.(-,0) D.(-∞,)
7. 如图组合体 中,为正方形
且边长为,面面,又,
,,,
则该组合体的体积为( )
A. B. C. D.
8.在长方体中,.
若分别为线段,的中点,则直线与
平面所成角的余弦值为( )
A. B. C. D.
9.由直线上的点向圆引切线,则切线长的最小值为 ( )
A. B. C. D.
10.过点作圆的弦,其中弦长为整数的共有( )
A.条 B.条 C.条 D.条
二、填空题(7个小题,每小题4分,共28分)
11.已知直线过点且直线的倾斜角为则直线的方程为 ________________.
12.与圆: 关于直线: 对称的圆的方程为_________.
13.考察下列三个命题,在“________”都缺少同一个条件,补上这个条件使其构成真命题(其中为不同直线,为不同平面),则此条件为______________.
① ; ② ; ③
14.如下图,在正方体中,
是中点,是的中点,则直线
与所成角的大小为_______.
15.已知直线和直线平行,则________.
16.圆上有四点到直线的距离为,则的取值范围为______________.
17.如图,在正四面体中,
分别是, ,的中心,
则在该正四面体各个面上的射影
所有可能的序号是________________.
① ② ③ ④
三.解答题
18.已知圆的圆心在直线上,且经过原点及点,求圆的方程.
19.在等腰中,,顶点为直线与轴交点且平分,
若,求 (1)直线的方程; (2)计算的面积.
20.如图,正方体的棱长为,为的中点.
(1)求证:AC⊥平面BDD1.
(2)求三棱锥的体积;
21、如图,已知三棱锥,,为中点,为中点,且是正三角形,.
(1)求证:平面;
(2)求证:平面平面;
22.已知圆:
(1)平面上有两点,求过点两点的直线被圆截得的弦长;
(2)已知过点的直线平分圆的周长,是直线上的动点,
并且,求的最小值.
(3) 若是轴上的动点,分别切圆于两点.
试问:直线是否恒过定点?如是,求出定点坐标,如不是,说明理由.
宁波万里国际学校中学
2011-2012学年度第一学期期中考试
[高二]年级 参考答案
选择题:
填空题:
11、 12、
13、 14、
15、 16、
17、③④
三、解答题:
18、解: 根据题意,设圆的方程为:
因为圆经过原点和,故此有:
…… ①
…… ②
两式联立,解得: ,
所以,所求的园的方程为:
19、解:根据题意知,又因为,平分,
所以两点关于直线对称,设
利用方程组我们容易得到
进而直线方程为:
(2)由点到直线距离公式得到到直线的距离为,又
所以,有
20.如图,正方体的棱长为,为的中点.
(1)求证:AC⊥平面BDD1.
(2)求三棱锥的体积;
略;
21、如图,已知三棱锥,,为中点,为中点,且是正三角形,.
(1)求证:平面;
(2)求证:平面平面;
略;
关键点就是证明
22.已知圆:
(1)平面上有两点,求过点两点的直线被圆截得的弦长;
(2)已知过点的直线平分圆的周长,是直线上的动点,
并且,求的最小值.
(3) 若是轴上的动点,分别切圆于两点.
试问:直线是否恒过定点?如是,求出定点坐标,如不是,说明理由.
解:(1)因为直线经过两点,从而直线的方程为
进而令中的得或
故此直线被圆截得的弦长为. …… 3分
(2) 因为圆的圆心为, 又直线过点,
所以直线的方程是:
而在直线上, 所以有: 也即有
, 进而有:
故当,即时,又,
从而时取得最小值
即直线恒过定点……………12分
D
P
M
C
B
A
座位号
D
P
M
C
B
A
同课章节目录
