平行四边形的性质
图片预览




文档简介
(共31张PPT)
数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 ——毕达哥拉斯
在数学课上,老师提出了这样一个问题,用20米的绳子围成平行四边形,且边长是正整数,有多少种围法?小明是个聪明的孩子,很快得出了答案,你知道答案了吗?这时候老师接着提问,如果长边比短边长2米,那将怎样呢
创设情境
19.1 平行四边形
—— 平行四边形的性质(第1课时)
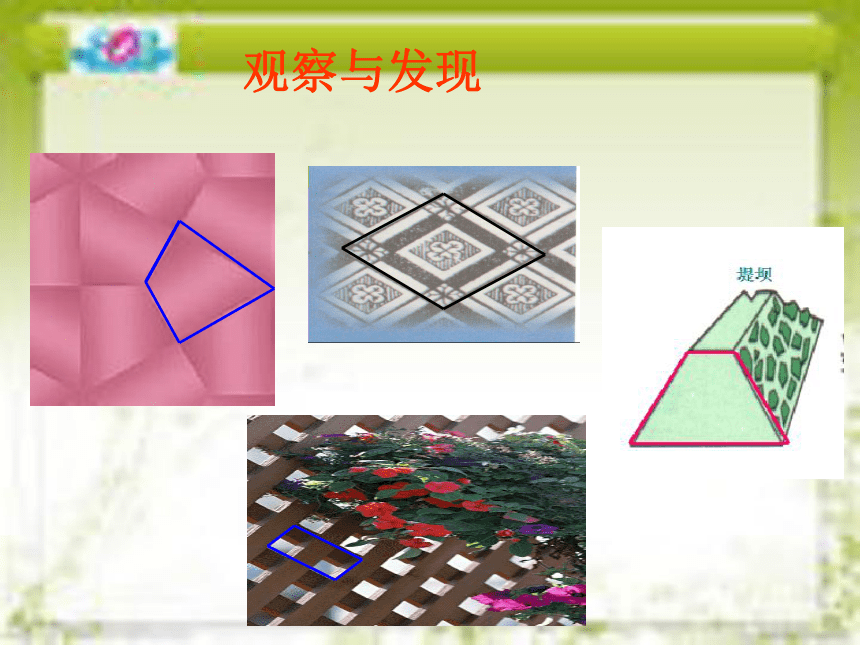
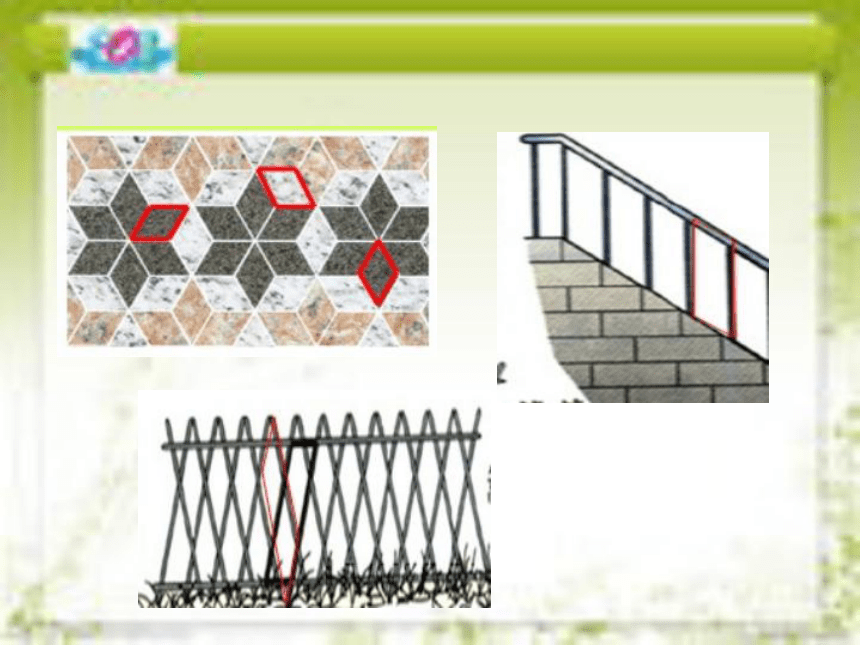
观察与发现
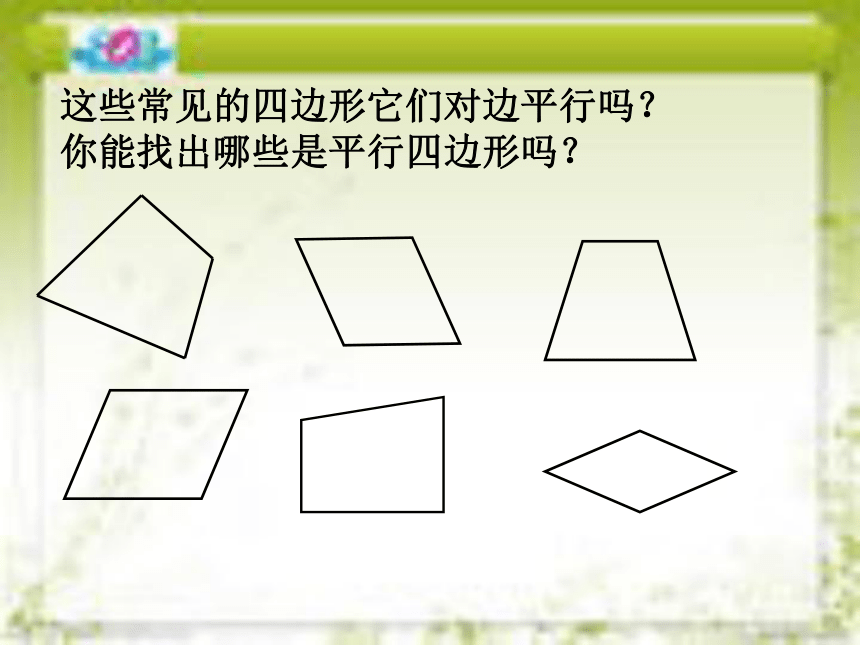
这些常见的四边形它们对边平行吗?
你能找出哪些是平行四边形吗?
四边形
两组对边分别平行的四边形叫做平行四边形.
定义
如图:四边形ABCD是平行四边形,
记作: ABCD
平行四边形的符号表示:
探索与发现
请你用你课前制作的平行四边形,进行观察与发现:
1.图中有哪些相等的角?
2.有哪些相等的边?
3.你能对你的猜想说明理由吗?
观察与猜想
1.相等的角有:
2.相等的边有:
∠A=∠C,∠B=∠D
AB=DC,AD=BC
验证结论
量一量:用直尺,量角器度量平行四边形的边和
角,得出AB=DC,AD=BC,∠A=∠C,∠B=∠D。
验证结论
剪一剪:把平行四边形沿着对角线剪开,叠合,得出两个完全重合的三角形。
小结:解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
2
1
3
4
验证结论
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳
例题:如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
⑴ 其他三条边各长多少?
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=200°
∴∠A=100°.
∵ AD∥BC
∴ ∠A+∠B=180°
∴ ∠B= 80°
A
D
B
C
应用举例
1.如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= 。
∠C= ∠D= .
3)若∠A+∠C=80°.则∠A= ;
∠D= 。
学以致用(定理的直接应用)
2.已知: ABCD,延长AB到E, 延长CD到F
使BE=DF
求证:AF=CE
学以致用(定理的综合应用)
3:在 ABCD中, ∠ABC 的平分线把对边分成4和3两部分,则这个平行四边形的周长是多少?
拓展与延伸(知识的综合应用)
如图:
通过探究,本节课你得到了哪些结论?
在探究平行四边形的性质过程中,你有哪些认识?
在运用平行四边形的性质解题时,你获得了什么思
想和方法?
感悟与收获
分层作业:
必做题:1.解决课前老师提出的问题。
2.教材习题19.1 1,2
选做题:(解决问题)农民李某想发展副业致 富,经考察地形后,在耕地旁边的荒地上开垦一平行四边形形状的鱼塘。能测得∠B=120° ,量得AD=50米,AB=80米。请你帮助李某计算一下鱼塘的对边AB、CD之间的距离及这个鱼塘的周长。
数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 ——毕达哥拉斯
在数学课上,老师提出了这样一个问题,用20米的绳子围成平行四边形,且边长是正整数,有多少种围法?小明是个聪明的孩子,很快得出了答案,你知道答案了吗?这时候老师接着提问,如果长边比短边长2米,那将怎样呢
创设情境
19.1 平行四边形
—— 平行四边形的性质(第1课时)
观察与发现
这些常见的四边形它们对边平行吗?
你能找出哪些是平行四边形吗?
四边形
两组对边分别平行的四边形叫做平行四边形.
定义
如图:四边形ABCD是平行四边形,
记作: ABCD
平行四边形的符号表示:
探索与发现
请你用你课前制作的平行四边形,进行观察与发现:
1.图中有哪些相等的角?
2.有哪些相等的边?
3.你能对你的猜想说明理由吗?
观察与猜想
1.相等的角有:
2.相等的边有:
∠A=∠C,∠B=∠D
AB=DC,AD=BC
验证结论
量一量:用直尺,量角器度量平行四边形的边和
角,得出AB=DC,AD=BC,∠A=∠C,∠B=∠D。
验证结论
剪一剪:把平行四边形沿着对角线剪开,叠合,得出两个完全重合的三角形。
小结:解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
2
1
3
4
验证结论
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳
例题:如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
⑴ 其他三条边各长多少?
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=200°
∴∠A=100°.
∵ AD∥BC
∴ ∠A+∠B=180°
∴ ∠B= 80°
A
D
B
C
应用举例
1.如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= 。
∠C= ∠D= .
3)若∠A+∠C=80°.则∠A= ;
∠D= 。
学以致用(定理的直接应用)
2.已知: ABCD,延长AB到E, 延长CD到F
使BE=DF
求证:AF=CE
学以致用(定理的综合应用)
3:在 ABCD中, ∠ABC 的平分线把对边分成4和3两部分,则这个平行四边形的周长是多少?
拓展与延伸(知识的综合应用)
如图:
通过探究,本节课你得到了哪些结论?
在探究平行四边形的性质过程中,你有哪些认识?
在运用平行四边形的性质解题时,你获得了什么思
想和方法?
感悟与收获
分层作业:
必做题:1.解决课前老师提出的问题。
2.教材习题19.1 1,2
选做题:(解决问题)农民李某想发展副业致 富,经考察地形后,在耕地旁边的荒地上开垦一平行四边形形状的鱼塘。能测得∠B=120° ,量得AD=50米,AB=80米。请你帮助李某计算一下鱼塘的对边AB、CD之间的距离及这个鱼塘的周长。
