正方形
图片预览




文档简介
(共23张PPT)
19.2.3 正方形
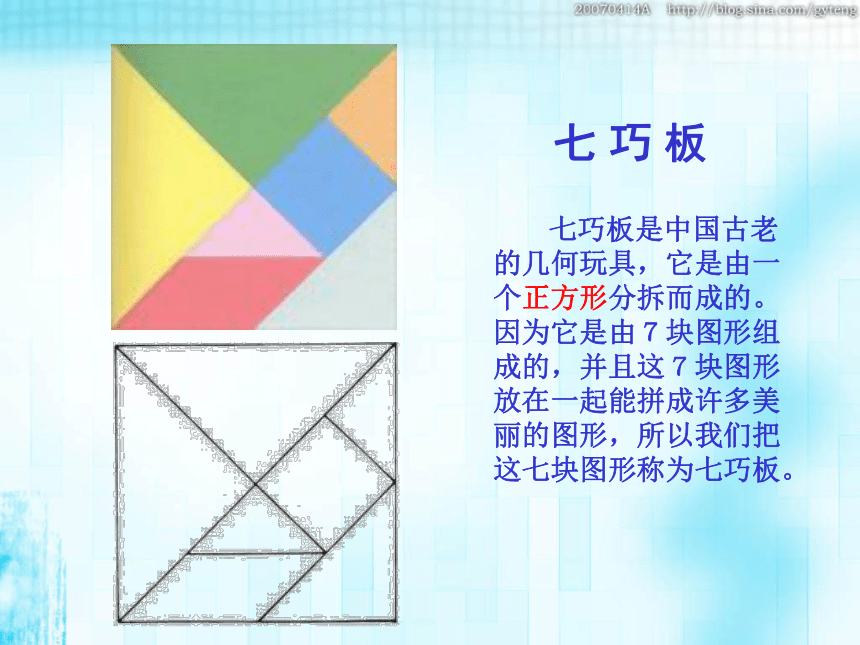
七 巧 板
七巧板是中国古老
的几何玩具,它是由一
个正方形分拆而成的。
因为它是由7块图形组
成的,并且这7块图形
放在一起能拼成许多美
丽的图形,所以我们把
这七块图形称为七巧板。
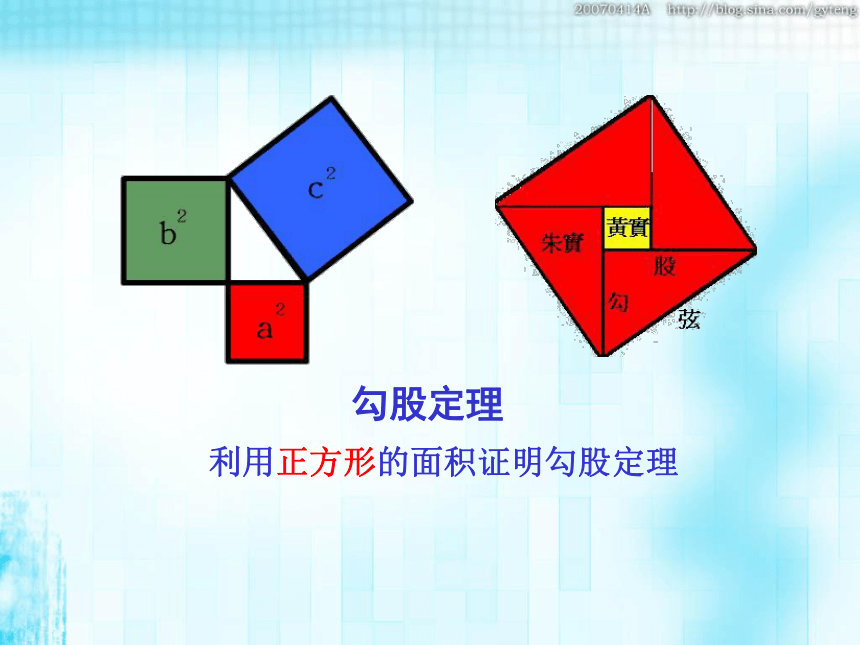
勾股定理
利用正方形的面积证明勾股定理
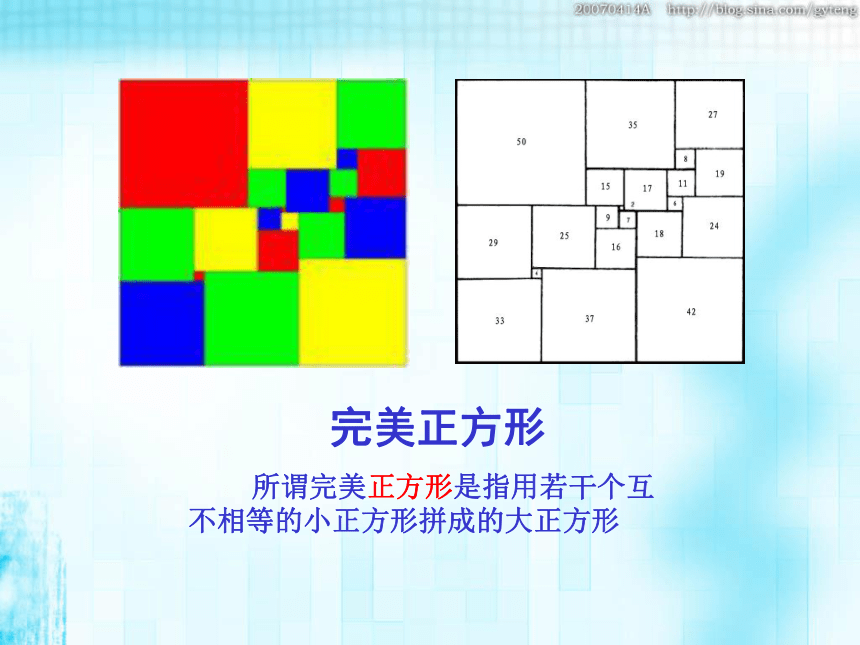
所谓完美正方形是指用若干个互不相等的小正方形拼成的大正方形
完美正方形
正 方 形
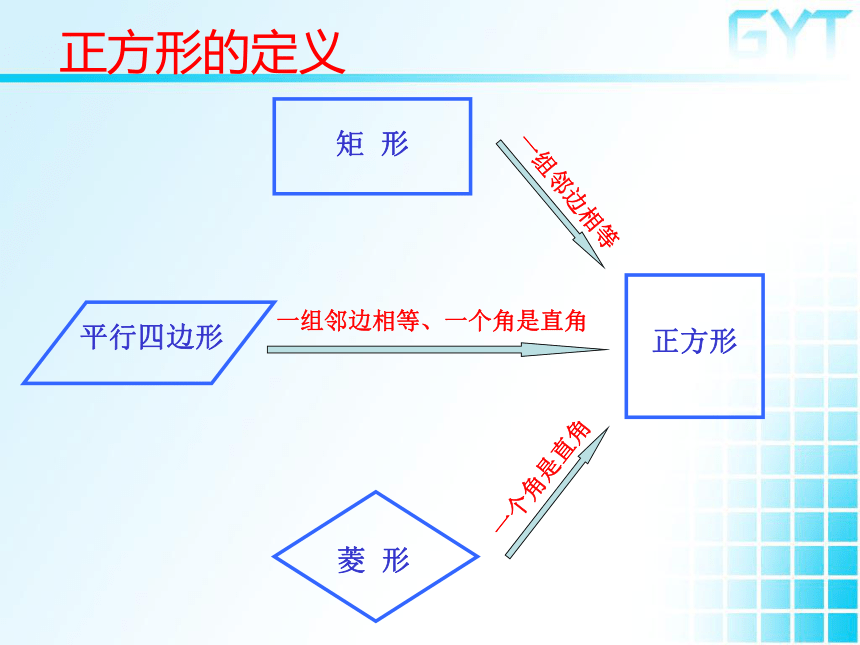
正方形的定义
矩 形
正方形
一组邻边相等
菱 形
一个角是直角
一组邻边相等、一个角是直角
平行四边形
正方形的定义
1、有一组邻边相等的矩形叫做正方形
2、有一个角是直角的菱形叫做正方形
3、有一组邻边相等且有一个角是直角
的平行四边形叫做正方形
正方形是特殊的平行四边形,
也是特殊的矩形,也是特殊的菱形。
正方形的性质 =
矩形性质
+
菱形性质
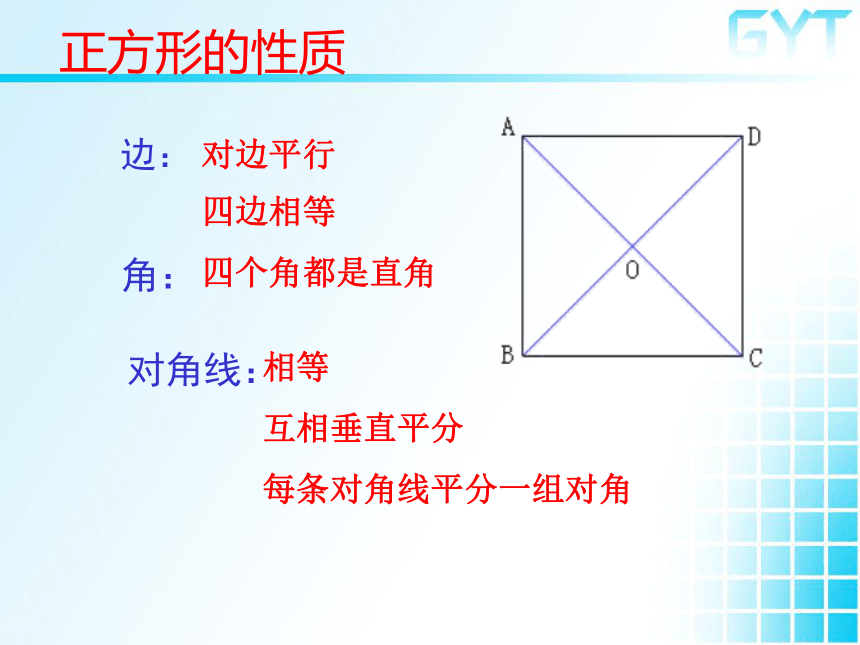
正方形的性质
边:
角:
对角线:
对边平行
四边相等
四个角都是直角
相等
互相垂直平分
每条对角线平分一组对角
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
讨论:平行四边形、矩形、菱形、正方形的关系
请用平行四边形、矩形、菱形、正方形
这四种图形填空
A
B
C
D
A表示:
B表示:
C表示:
D表示:
平行四边形
矩形(菱形)
菱形(矩形)
正 方 形
小红在店里看到一块漂亮的方纱巾,非常想买。但她拿起来看时感觉不太方。商店老板看她犹豫的样子,马上过来拉起一组对角,让小红看这组对角是否对齐,小红还有些犹豫,老板又拉起另一组对角,让小红检验。小红终于买了这块纱巾。你认为小红买的这块纱巾真是正方形吗?你能帮她检验吗?
探究:
讨 论
具备什么条件的矩形是正方形?
具备什么条件的菱形是正方形?
可从边,角,对角线上考虑
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
正方形的判定
1 定义法:
2、 对角线法:
两条对角线互相垂直的矩形是正方形
有一组邻边相等的矩形是正方形。
有一个角是直角的菱形是正方形。
3、矩形菱形法:
既是矩形又是菱形的四边形是正方形。
两条对角线相等的菱形是正方形
练 一 练
满足下列条件的四边形是不是正方形:
1、对角线互相垂直且相等的平行四边形;
2、对角线互相垂直的矩形;
3、对角线相等的菱形;
4、对角线互相垂直平分且相等的四边形.
判定正方形要准备的条件:
平 行 四 边 形
一组邻边相等
一个角是直角
实际问题
1、把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
2、如果是一个长方形木板,又如何从中裁出一个最大的正方形木板呢?
A
B
C
D
拓展讨论
1、图中有多少个等腰直角三角形?
2、正方形ABCD有多少条对称轴?
(8个)
(4条)
正方形既是轴对称图形又是中心对称图形
已知:如图正方形ABCD对角线AC、BD
相交于点O。
求证: △ABO ≌ △BCO ≌ △CDO ≌△DAO
例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
范例精讲
证明:∵四边形ABCD是正方形
∴AO=BO=CO=DO
∴ △ABO 、 △BCO 、△CDO 、△DAO
都是等腰直角三角形,并且
△ABO ≌ △BCO ≌ △CDO ≌△DAO
例题解析
例2. 如图,在正方ABCD中,求∠ABD、∠DAC、∠DOC的度数。
解:
∵ 四边形ABCD是正方形
根据正方形的四个内角都为直角
又因为正方形的对角线平分内角
又∵正方形的两条对角线互相垂直
即AC⊥BD
O
A
B
C
D
得∠DAB=∠ABC=90°
即AC平分∠BAD,BD平分∠ABC
∴ ∠ABD=∠DAC= × 90°=45°
∴∠DOC=90°
2
1
课堂练习
45°
正方形
12cm
2a+1
1.正方形的一边和对角线的夹角为___________.
2.如果一个四边形既是菱形又是矩形,那么它一定是_________.
3.已知正方形的面积为9cm,它的周长为 _______________.
4.正方形的边长为a,当边长增加1时,其面积增加了__________.
O
A
B
C
D
课时小结
图 形
性 质 平 行
四边形 矩 形 菱 形 正方形
对边平行且相等
四条边都相等
对角相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
每条对角线平分一组对角
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
19.2.3 正方形
七 巧 板
七巧板是中国古老
的几何玩具,它是由一
个正方形分拆而成的。
因为它是由7块图形组
成的,并且这7块图形
放在一起能拼成许多美
丽的图形,所以我们把
这七块图形称为七巧板。
勾股定理
利用正方形的面积证明勾股定理
所谓完美正方形是指用若干个互不相等的小正方形拼成的大正方形
完美正方形
正 方 形
正方形的定义
矩 形
正方形
一组邻边相等
菱 形
一个角是直角
一组邻边相等、一个角是直角
平行四边形
正方形的定义
1、有一组邻边相等的矩形叫做正方形
2、有一个角是直角的菱形叫做正方形
3、有一组邻边相等且有一个角是直角
的平行四边形叫做正方形
正方形是特殊的平行四边形,
也是特殊的矩形,也是特殊的菱形。
正方形的性质 =
矩形性质
+
菱形性质
正方形的性质
边:
角:
对角线:
对边平行
四边相等
四个角都是直角
相等
互相垂直平分
每条对角线平分一组对角
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
讨论:平行四边形、矩形、菱形、正方形的关系
请用平行四边形、矩形、菱形、正方形
这四种图形填空
A
B
C
D
A表示:
B表示:
C表示:
D表示:
平行四边形
矩形(菱形)
菱形(矩形)
正 方 形
小红在店里看到一块漂亮的方纱巾,非常想买。但她拿起来看时感觉不太方。商店老板看她犹豫的样子,马上过来拉起一组对角,让小红看这组对角是否对齐,小红还有些犹豫,老板又拉起另一组对角,让小红检验。小红终于买了这块纱巾。你认为小红买的这块纱巾真是正方形吗?你能帮她检验吗?
探究:
讨 论
具备什么条件的矩形是正方形?
具备什么条件的菱形是正方形?
可从边,角,对角线上考虑
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
正方形的判定
1 定义法:
2、 对角线法:
两条对角线互相垂直的矩形是正方形
有一组邻边相等的矩形是正方形。
有一个角是直角的菱形是正方形。
3、矩形菱形法:
既是矩形又是菱形的四边形是正方形。
两条对角线相等的菱形是正方形
练 一 练
满足下列条件的四边形是不是正方形:
1、对角线互相垂直且相等的平行四边形;
2、对角线互相垂直的矩形;
3、对角线相等的菱形;
4、对角线互相垂直平分且相等的四边形.
判定正方形要准备的条件:
平 行 四 边 形
一组邻边相等
一个角是直角
实际问题
1、把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
2、如果是一个长方形木板,又如何从中裁出一个最大的正方形木板呢?
A
B
C
D
拓展讨论
1、图中有多少个等腰直角三角形?
2、正方形ABCD有多少条对称轴?
(8个)
(4条)
正方形既是轴对称图形又是中心对称图形
已知:如图正方形ABCD对角线AC、BD
相交于点O。
求证: △ABO ≌ △BCO ≌ △CDO ≌△DAO
例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
范例精讲
证明:∵四边形ABCD是正方形
∴AO=BO=CO=DO
∴ △ABO 、 △BCO 、△CDO 、△DAO
都是等腰直角三角形,并且
△ABO ≌ △BCO ≌ △CDO ≌△DAO
例题解析
例2. 如图,在正方ABCD中,求∠ABD、∠DAC、∠DOC的度数。
解:
∵ 四边形ABCD是正方形
根据正方形的四个内角都为直角
又因为正方形的对角线平分内角
又∵正方形的两条对角线互相垂直
即AC⊥BD
O
A
B
C
D
得∠DAB=∠ABC=90°
即AC平分∠BAD,BD平分∠ABC
∴ ∠ABD=∠DAC= × 90°=45°
∴∠DOC=90°
2
1
课堂练习
45°
正方形
12cm
2a+1
1.正方形的一边和对角线的夹角为___________.
2.如果一个四边形既是菱形又是矩形,那么它一定是_________.
3.已知正方形的面积为9cm,它的周长为 _______________.
4.正方形的边长为a,当边长增加1时,其面积增加了__________.
O
A
B
C
D
课时小结
图 形
性 质 平 行
四边形 矩 形 菱 形 正方形
对边平行且相等
四条边都相等
对角相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
每条对角线平分一组对角
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
