平行四边形的性质课件
图片预览




文档简介
(共41张PPT)
在数学的天地里,重要的不是我们知道什么,
而是我们怎么知道什么。
——毕达哥拉斯 (古希腊著名的哲学家、数学家、天文学家)
§19.1 .1平行四边形的性质
平行四边形
将两张全等的三角形纸片,设法找到某一边的中点,记作点O,将上层的三角形纸片绕点O旋转180度,下层的三角形纸片保持不动,此时:
(1)两张纸片拼成了怎样的图形?
(2)这个图形中有哪些相等的角?有没有互相平行的线段?你是怎样得到的?
(3)用简洁的语言刻画这个图形的特征, 并与同伴交流。
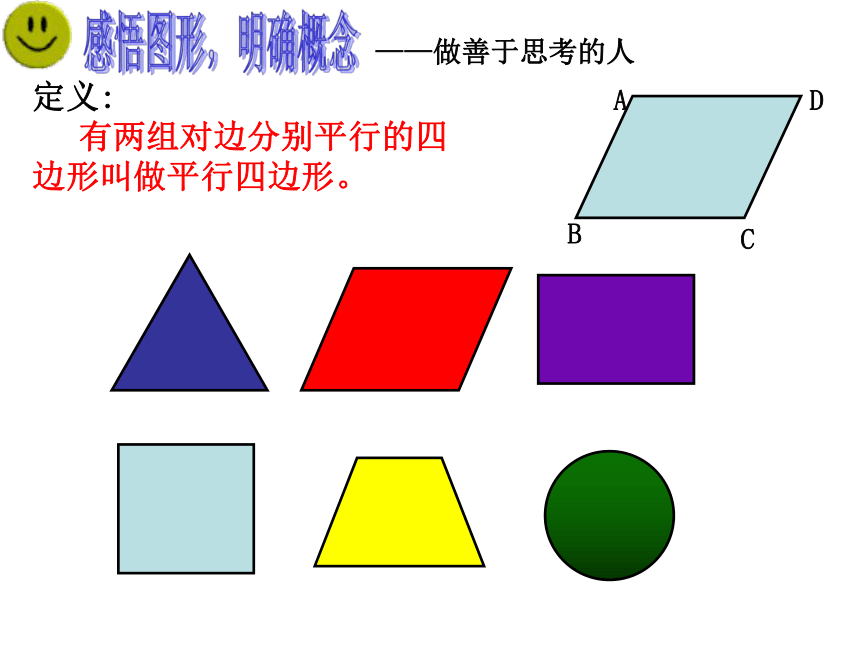
定义:
有两组对边分别平行的四边形叫做平行四边形。
A
B
C
D
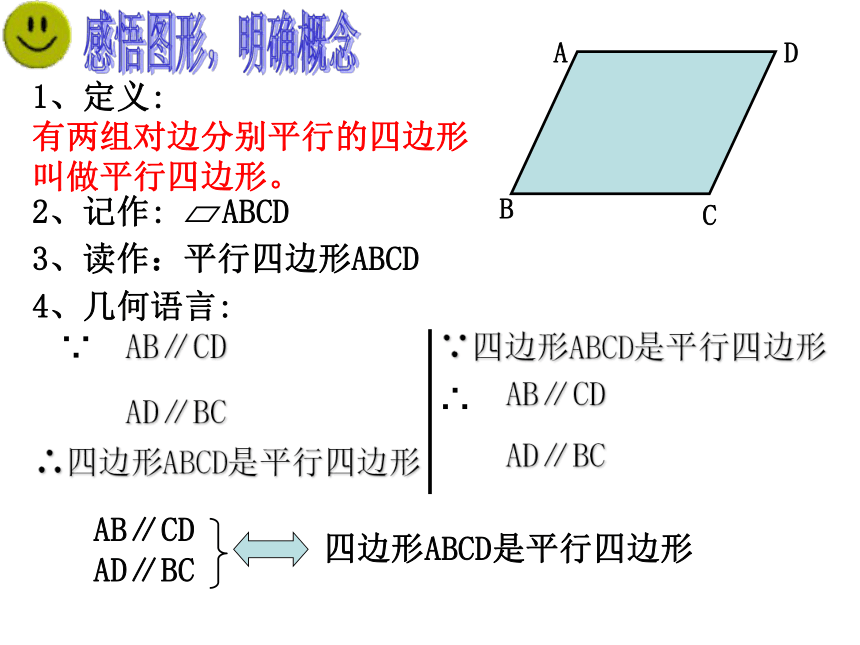
1、定义:
有两组对边分别平行的四边形 叫做平行四边形。
2、记作:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
A
B
C
D
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
四边形ABCD是平行四边形
AB∥CD AD∥BC
A
B
C
D
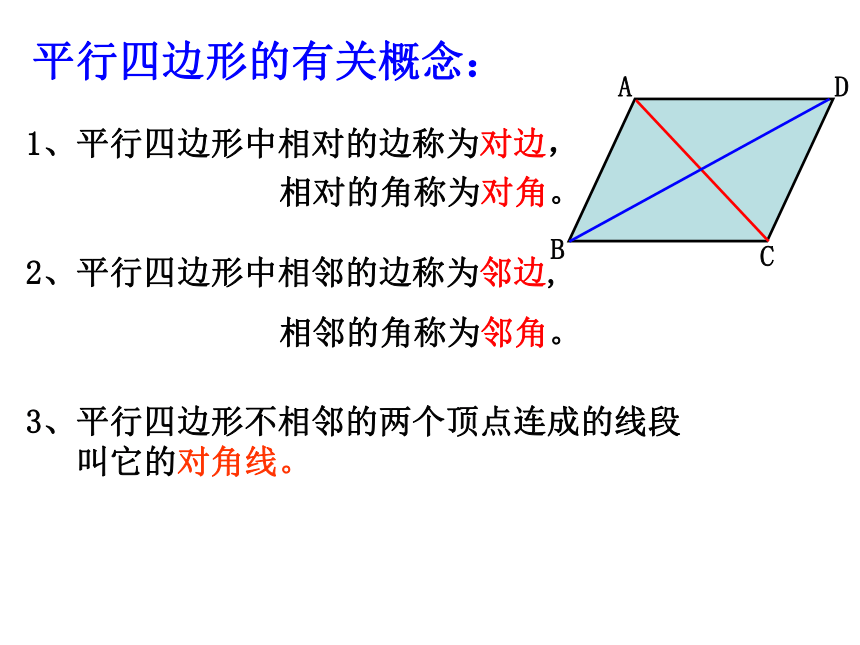
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。
质疑:
平行四边形除以上性质外还有其他性质吗?
探索要求:
1、借助手中的平行四边形纸片、刻度尺、量角器、剪刀等学具;
2、小组合作学习探索;用测量、旋转、平移、推理等方法验证猜想.
3、把探索过程中得到的结论写在成果展示卡上.
猜一猜:平行四边形的性质还有哪些?
画一画:在格点纸上画一个平行四边形
A
B
D
C
平行四边形的画法:
剪一剪:将你所画的平行四边形沿其中一条对角线剪开,现在,你有新的办法进一步验证猜想吗?
猜一猜:平行四边形的性质还有哪些?
画一画:在格点纸上画一个平行四边形
量一量:度量一下,与你的猜想一致吗?
A
B
C
D
(1)平行四边形的对边相等.
推理论证 :
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
证明:
(2)平行四边形的对角相等.
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
证明:
A
B
C
D
定理1:平行四边形的对边相等.
如图,在□ABCD中,
AB=CD,AD=BC.
推理格式:
∵四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.
A
B
C
D
定理2:平行四边形的对角相等.
如图,在□ABCD中,
∠A=∠C,∠B=∠D.
推理格式:
∵四边形ABCD是平行四边形,
∴ ∠A=∠C,∠B=∠D.
A
B
C
D
例1 :在平行四边形ABCD中,已
知∠A =32°,求其余三个角的度数。
解:∵四边形ABCD是平行四边形且 ∠A=32°
∴ ∠A =∠C=32°, ∠B=∠D
(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴ ∠A +∠B =180°
(两直线平行,同旁内角互补)
∴ ∠B=∠D= 180°-∠A
= 180°- 32°=148°
例2 :已知在平行四边形 ABCD中,AB=6cm,
BC=4cm,求平行四边形ABCD 的周长。
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD
(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴平行四边形ABCD的周长
=AB+CD+BC+AD
=6+6+4+4=20(cm)
1、有一块平行四边形的绿地,
测得∠A=60 ,请你求∠D的
度数。
解:
∵四边形ABCD是平行四边形
∴ DC ∥ AB( )
∴ ∠D +∠A = __ ( )
∵ ∠A = 60
∴ ∠D = ____
2、学校准备修建一个平行四边形的花坛,如图,想使其中一个角为56°,一边长30m,另一边长25m.
求:
(1)∠ADC,∠BCD的度数.
(2)边AB,BC的长度.
A
B
C
D
56°
30m
25m
3、平行四边形ABCD的周长为40cm,△ABC的周长为 25cm ,则对角线AC长为 ( )cm.
B
A
D
C
4、辩一辩:谁的测量肯定有误?
甲、乙、丙、丁四位同学正在
测量 ABCD,
甲测量的结果:AB=CD=5,BC=AD=8
乙测量的结果:∠A=∠C=40°,
∠B=∠D=130°
丙测量的结果:AB∥CD ,AD∥BC
丁测量的结果:∠A:∠B:∠C:∠D=2:6:2:7
A
B
C
D
1、请你谈谈本节课的收获是什么
2、你还有什么遗憾吗?
1. 必做题:
教材 90页 1、2题
2.选做题:
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
七、布置作业:
A
B
C
教师寄语:
踏上一段新的旅程,
体验一种新的学习,
走进一种新的生活,
塑造一个新的自我,
发现一个新的理想,
感受学习的快乐!
在数学的天地里,重要的不是我们知道什么,
而是我们怎么知道什么。
——毕达哥拉斯 (古希腊著名的哲学家、数学家、天文学家)
§19.1 .1平行四边形的性质
平行四边形
将两张全等的三角形纸片,设法找到某一边的中点,记作点O,将上层的三角形纸片绕点O旋转180度,下层的三角形纸片保持不动,此时:
(1)两张纸片拼成了怎样的图形?
(2)这个图形中有哪些相等的角?有没有互相平行的线段?你是怎样得到的?
(3)用简洁的语言刻画这个图形的特征, 并与同伴交流。
定义:
有两组对边分别平行的四边形叫做平行四边形。
A
B
C
D
1、定义:
有两组对边分别平行的四边形 叫做平行四边形。
2、记作:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
A
B
C
D
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
四边形ABCD是平行四边形
AB∥CD AD∥BC
A
B
C
D
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。
质疑:
平行四边形除以上性质外还有其他性质吗?
探索要求:
1、借助手中的平行四边形纸片、刻度尺、量角器、剪刀等学具;
2、小组合作学习探索;用测量、旋转、平移、推理等方法验证猜想.
3、把探索过程中得到的结论写在成果展示卡上.
猜一猜:平行四边形的性质还有哪些?
画一画:在格点纸上画一个平行四边形
A
B
D
C
平行四边形的画法:
剪一剪:将你所画的平行四边形沿其中一条对角线剪开,现在,你有新的办法进一步验证猜想吗?
猜一猜:平行四边形的性质还有哪些?
画一画:在格点纸上画一个平行四边形
量一量:度量一下,与你的猜想一致吗?
A
B
C
D
(1)平行四边形的对边相等.
推理论证 :
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
证明:
(2)平行四边形的对角相等.
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
证明:
A
B
C
D
定理1:平行四边形的对边相等.
如图,在□ABCD中,
AB=CD,AD=BC.
推理格式:
∵四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.
A
B
C
D
定理2:平行四边形的对角相等.
如图,在□ABCD中,
∠A=∠C,∠B=∠D.
推理格式:
∵四边形ABCD是平行四边形,
∴ ∠A=∠C,∠B=∠D.
A
B
C
D
例1 :在平行四边形ABCD中,已
知∠A =32°,求其余三个角的度数。
解:∵四边形ABCD是平行四边形且 ∠A=32°
∴ ∠A =∠C=32°, ∠B=∠D
(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴ ∠A +∠B =180°
(两直线平行,同旁内角互补)
∴ ∠B=∠D= 180°-∠A
= 180°- 32°=148°
例2 :已知在平行四边形 ABCD中,AB=6cm,
BC=4cm,求平行四边形ABCD 的周长。
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD
(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴平行四边形ABCD的周长
=AB+CD+BC+AD
=6+6+4+4=20(cm)
1、有一块平行四边形的绿地,
测得∠A=60 ,请你求∠D的
度数。
解:
∵四边形ABCD是平行四边形
∴ DC ∥ AB( )
∴ ∠D +∠A = __ ( )
∵ ∠A = 60
∴ ∠D = ____
2、学校准备修建一个平行四边形的花坛,如图,想使其中一个角为56°,一边长30m,另一边长25m.
求:
(1)∠ADC,∠BCD的度数.
(2)边AB,BC的长度.
A
B
C
D
56°
30m
25m
3、平行四边形ABCD的周长为40cm,△ABC的周长为 25cm ,则对角线AC长为 ( )cm.
B
A
D
C
4、辩一辩:谁的测量肯定有误?
甲、乙、丙、丁四位同学正在
测量 ABCD,
甲测量的结果:AB=CD=5,BC=AD=8
乙测量的结果:∠A=∠C=40°,
∠B=∠D=130°
丙测量的结果:AB∥CD ,AD∥BC
丁测量的结果:∠A:∠B:∠C:∠D=2:6:2:7
A
B
C
D
1、请你谈谈本节课的收获是什么
2、你还有什么遗憾吗?
1. 必做题:
教材 90页 1、2题
2.选做题:
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
七、布置作业:
A
B
C
教师寄语:
踏上一段新的旅程,
体验一种新的学习,
走进一种新的生活,
塑造一个新的自我,
发现一个新的理想,
感受学习的快乐!
