2021-2022学年人教版九年级数学上册 21.2.4 一元二次方程的根与系数的关系 课件(60张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册 21.2.4 一元二次方程的根与系数的关系 课件(60张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览









文档简介
一元二次方程的根与系数的关系
教学目标
了解一元二次方程的根与系数关系,能进行简单应用.
在一元二次方程根与系数关系的探究过程中,感受由特殊
到一般的认识方法.
教学重点
一元二次方程根与系数的关系的探究及简单应用.
根与系数关系的应用.
教学难点
知识回顾
一元二次方程的一般形式是什么?
一元二次方程的求根公式是什么?
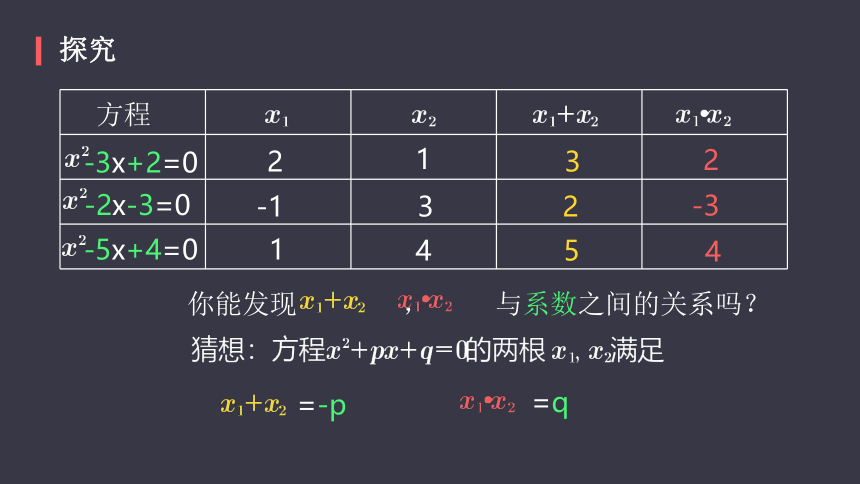
探究
方程
-3x+2=0
-2x-3=0
-5x+4=0
2
1
3
2
-1
3
2
-3
1
4
5
4
你能发现? ? ? ? ? ? ?,? ? ? ? 与系数之间的关系吗?
=-p
=q
思考
=-p
=q
思考
=-p
=q
它的两根之和,两根之积
与系数a、b、c之间又有什么样的关系呢?
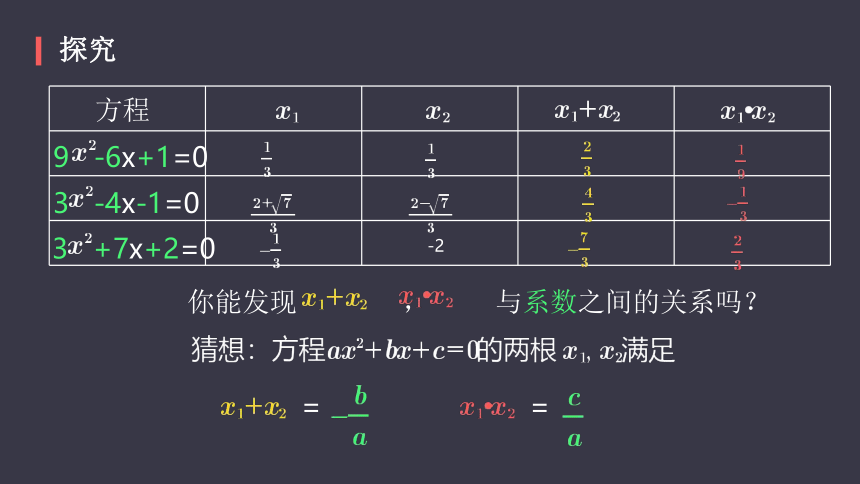
探究
方程
9? ?-6x+1=0
3? ?-4x-1=0
3? ?+7x+2=0
-2
你能发现? ? ? ? ? ? ?,? ? ? ? 与系数之间的关系吗?
=
=
证明
根据求根公式可知:
=
=
根据求根公式可知:
证明
=
=
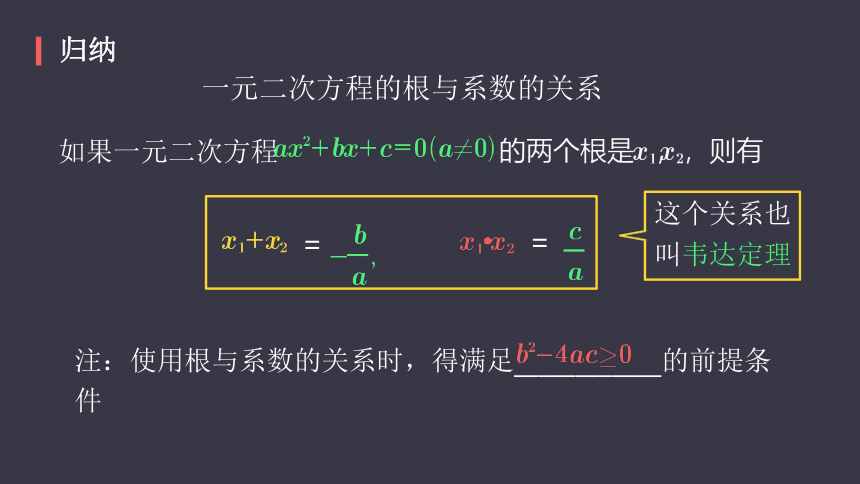
归纳
一元二次方程的根与系数的关系
如果一元二次方程
=
=
这个关系也
叫韦达定理
注:使用根与系数的关系时,得满足____________的前提条件
? ? ? ?韦达是法国十六世纪最有影响的数学家之一.
第一个引进系统的代数符号,并对方程论做了改进.?
? ? ? ? 他生于法国的普瓦图.年轻时学习法律当过律师,
后从事政治活动,当过议会的议员,在对西班牙的战
争中曾为政府破译敌军的密码.
? ? ? ? 韦达还致力于数学研究,第一个有意识和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步.韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”).
? ? ? ? 韦达在欧洲被尊称为“代数学之父”.
韦达(1540-1603)
例题
根据一元二次方程根与系数的关系,
求下列方程两根的和与积:
根据一元二次方程根与系数的关系,
求下列方程两根的和与积:
例题
根据一元二次方程根与系数的关系,
求下列方程两根的和与积:
例题
能直接看出
a、b、c吗?
不能,得先化为一般式
归纳
使用根与系数关系求两根之和或两根之积时需要注意什么?
1.如果方程不是一般形式,一定要先变为____________.
一般形式
2.一定要牢记公式.特别的,使用
时,
注意不要把_______漏了.
“-”
练习
不解方程,求下列方程两个根的和与积:
练习
当m=________时,此方程的两根互为相反数.
当m=________时,此方程的两根互为倒数.
-1
1
练习
不解方程,求下列方程两个根的和与积:
总结
这节课我们学到了什么?
一元二次方程的根与系数的关系
如果一元二次方程
=
=
这个关系也
叫韦达定理
注:使用根与系数的关系时,得满足____________的前提条件
已知一根求另一根
提示:可以直接把根代入,也可以利用两根之积直接求另一根.
已知一根求另一根
-3
已知一根求另一根
答案:另一根是-1,m=-2.
求两根的对称式
=3
求两根的对称式
4
1
14
12
求两根的对称式
(1)7
求两根的对称式
(4)3
求两根的对称式
(6)10
归纳总结
常见的两根对称式求值
已知对称式反求参数
答案:k=-2.
注:使用根与系数的关系时,得满足____________的前提条件
求两根之差的绝对值
答案:k的值为9或-3.
归纳总结
已知两根构造方程
求一个一元二次方程,使它的两个根是2和3,且二次项系数为1.
提示:利用根与系数关系直接求出系数.
已知两根构造方程
求一个一元二次方程,使它的两个根是2和3,且二次项系数为5.
提示:利用根与系数关系直接求出系数.
已知两根构造方程
以2和-3为根的一元二次方程(二次项系数为1)为________.
提示:利用根与系数关系直接求出系数.
看错类问题
小明和小敏解同一个一元二次方程时,小明看错了一次项系数所
求出的根为-9和-1;小敏看错了常数项所求出的根是8和2.你
知道原来的方程是什么吗?
提示1:把精力放在没看错的系数上.
提示2:可以假设二次项系数为1.
看错类问题
甲、乙二人解同一个一元二次方程时,甲看错了常数项所求出
的根为1,4;乙看错了一次项系数所求出的根是-2,-3.则
这个一元二次方程为________________??
提示1:把精力放在没看错的系数上.
提示2:可以假设二次项系数为1.
已知两个数的和与积求这两个数
已知两个数的和是1,积是-2,则两个数分别是多少?
提示:可以把这两个数看作某个一元二次方程的两根.
答案:2,-1.
已知根的范围求参数范围
一正根,一负根
两个正根
两个负根
已知根的范围求参数范围
解: 由已知,
即
已知根的范围求参数范围
已知根的范围求参数范围
已知根的范围求参数范围
提示:需要分类讨论
已知根的范围求参数范围
(1)求证:无论m取何值时,方程总有两不相等的实数根.
(2)当m取何值时,方程的一根大于1,另一根小于1?
分析: (1) 列出△的代数式,证其恒大于零? ? ?
复习巩固
1.解下列方程:
复习巩固
2.填空:
复习巩固
3. 用配方法解下列方程:
复习巩固
4. 利用判别式判断下列方程的根的情况:
复习巩固
5. 用公式法解下列方程:
复习巩固
6. 用因式分解法解下列方程:
复习巩固
7. 求下列方程两个根的和与积:
综合运用
综合运用
9. 参加一次商品交易会的每两家公司之间都签订了一份合同,
? ? 所有公司共签订了45 份合同,共有多少家公司参加商品交
? ? 易会??
综合运用
综合运用
拓广探索
12. 一个凸多边形共有20条对角线,它是几边形?是否存在有
? ? ? 18条对角线的多边形?如果存在,它是几边形?如果不存
? ? ? 在,说明得出结论的道理.??
拓广探索
黄金分割数
? ? ? ?本章引言中有一个关于人体雕塑的问题.? 要使雕像的上部(腰以上)与下部(腰以下)的高度比, 等于下部与全部(全身)的高度比,这个高度比应是多少?? ? ? ?? ? ?把上面的问题一般化, 如图1, 在线段AB上找一个点C, C 把AB?分为AC 和CB?
两段,其中AC 是较小的一段,现要使AC :CB=CB : AB. 为简单起见, 设AB=1, CB=x, 则AC=1一x. 代入AC :CB=CB : AB,即(1-x):x=x:1,也即
A
C
B
1-x
x
图1
黄金分割数
图2
A
B
C
D
E
M
N
黄金分割数
? ? ? ?长期以来,很多人认为黄金分割数是一个很特别的数. 一
些美术家认为: 如果人的上、下身长之比接近黄金分割数, 那
么可以增加美感. 据说,一些名画和雕塑中的人体大都符合这
个比,一位科学家曾提出: 在一棵树的生长过程中,??
? ? ? ?优选法是一种具有广泛应用价值的数学方法,著名数学家
华罗庚曾为普及它作出重要贡献. 优选法中有一种0.618法应用
了黄金分割数. 同学们可以查阅资料,了解0.618法的应用.
教学目标
了解一元二次方程的根与系数关系,能进行简单应用.
在一元二次方程根与系数关系的探究过程中,感受由特殊
到一般的认识方法.
教学重点
一元二次方程根与系数的关系的探究及简单应用.
根与系数关系的应用.
教学难点
知识回顾
一元二次方程的一般形式是什么?
一元二次方程的求根公式是什么?
探究
方程
-3x+2=0
-2x-3=0
-5x+4=0
2
1
3
2
-1
3
2
-3
1
4
5
4
你能发现? ? ? ? ? ? ?,? ? ? ? 与系数之间的关系吗?
=-p
=q
思考
=-p
=q
思考
=-p
=q
它的两根之和,两根之积
与系数a、b、c之间又有什么样的关系呢?
探究
方程
9? ?-6x+1=0
3? ?-4x-1=0
3? ?+7x+2=0
-2
你能发现? ? ? ? ? ? ?,? ? ? ? 与系数之间的关系吗?
=
=
证明
根据求根公式可知:
=
=
根据求根公式可知:
证明
=
=
归纳
一元二次方程的根与系数的关系
如果一元二次方程
=
=
这个关系也
叫韦达定理
注:使用根与系数的关系时,得满足____________的前提条件
? ? ? ?韦达是法国十六世纪最有影响的数学家之一.
第一个引进系统的代数符号,并对方程论做了改进.?
? ? ? ? 他生于法国的普瓦图.年轻时学习法律当过律师,
后从事政治活动,当过议会的议员,在对西班牙的战
争中曾为政府破译敌军的密码.
? ? ? ? 韦达还致力于数学研究,第一个有意识和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步.韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”).
? ? ? ? 韦达在欧洲被尊称为“代数学之父”.
韦达(1540-1603)
例题
根据一元二次方程根与系数的关系,
求下列方程两根的和与积:
根据一元二次方程根与系数的关系,
求下列方程两根的和与积:
例题
根据一元二次方程根与系数的关系,
求下列方程两根的和与积:
例题
能直接看出
a、b、c吗?
不能,得先化为一般式
归纳
使用根与系数关系求两根之和或两根之积时需要注意什么?
1.如果方程不是一般形式,一定要先变为____________.
一般形式
2.一定要牢记公式.特别的,使用
时,
注意不要把_______漏了.
“-”
练习
不解方程,求下列方程两个根的和与积:
练习
当m=________时,此方程的两根互为相反数.
当m=________时,此方程的两根互为倒数.
-1
1
练习
不解方程,求下列方程两个根的和与积:
总结
这节课我们学到了什么?
一元二次方程的根与系数的关系
如果一元二次方程
=
=
这个关系也
叫韦达定理
注:使用根与系数的关系时,得满足____________的前提条件
已知一根求另一根
提示:可以直接把根代入,也可以利用两根之积直接求另一根.
已知一根求另一根
-3
已知一根求另一根
答案:另一根是-1,m=-2.
求两根的对称式
=3
求两根的对称式
4
1
14
12
求两根的对称式
(1)7
求两根的对称式
(4)3
求两根的对称式
(6)10
归纳总结
常见的两根对称式求值
已知对称式反求参数
答案:k=-2.
注:使用根与系数的关系时,得满足____________的前提条件
求两根之差的绝对值
答案:k的值为9或-3.
归纳总结
已知两根构造方程
求一个一元二次方程,使它的两个根是2和3,且二次项系数为1.
提示:利用根与系数关系直接求出系数.
已知两根构造方程
求一个一元二次方程,使它的两个根是2和3,且二次项系数为5.
提示:利用根与系数关系直接求出系数.
已知两根构造方程
以2和-3为根的一元二次方程(二次项系数为1)为________.
提示:利用根与系数关系直接求出系数.
看错类问题
小明和小敏解同一个一元二次方程时,小明看错了一次项系数所
求出的根为-9和-1;小敏看错了常数项所求出的根是8和2.你
知道原来的方程是什么吗?
提示1:把精力放在没看错的系数上.
提示2:可以假设二次项系数为1.
看错类问题
甲、乙二人解同一个一元二次方程时,甲看错了常数项所求出
的根为1,4;乙看错了一次项系数所求出的根是-2,-3.则
这个一元二次方程为________________??
提示1:把精力放在没看错的系数上.
提示2:可以假设二次项系数为1.
已知两个数的和与积求这两个数
已知两个数的和是1,积是-2,则两个数分别是多少?
提示:可以把这两个数看作某个一元二次方程的两根.
答案:2,-1.
已知根的范围求参数范围
一正根,一负根
两个正根
两个负根
已知根的范围求参数范围
解: 由已知,
即
已知根的范围求参数范围
已知根的范围求参数范围
已知根的范围求参数范围
提示:需要分类讨论
已知根的范围求参数范围
(1)求证:无论m取何值时,方程总有两不相等的实数根.
(2)当m取何值时,方程的一根大于1,另一根小于1?
分析: (1) 列出△的代数式,证其恒大于零? ? ?
复习巩固
1.解下列方程:
复习巩固
2.填空:
复习巩固
3. 用配方法解下列方程:
复习巩固
4. 利用判别式判断下列方程的根的情况:
复习巩固
5. 用公式法解下列方程:
复习巩固
6. 用因式分解法解下列方程:
复习巩固
7. 求下列方程两个根的和与积:
综合运用
综合运用
9. 参加一次商品交易会的每两家公司之间都签订了一份合同,
? ? 所有公司共签订了45 份合同,共有多少家公司参加商品交
? ? 易会??
综合运用
综合运用
拓广探索
12. 一个凸多边形共有20条对角线,它是几边形?是否存在有
? ? ? 18条对角线的多边形?如果存在,它是几边形?如果不存
? ? ? 在,说明得出结论的道理.??
拓广探索
黄金分割数
? ? ? ?本章引言中有一个关于人体雕塑的问题.? 要使雕像的上部(腰以上)与下部(腰以下)的高度比, 等于下部与全部(全身)的高度比,这个高度比应是多少?? ? ? ?? ? ?把上面的问题一般化, 如图1, 在线段AB上找一个点C, C 把AB?分为AC 和CB?
两段,其中AC 是较小的一段,现要使AC :CB=CB : AB. 为简单起见, 设AB=1, CB=x, 则AC=1一x. 代入AC :CB=CB : AB,即(1-x):x=x:1,也即
A
C
B
1-x
x
图1
黄金分割数
图2
A
B
C
D
E
M
N
黄金分割数
? ? ? ?长期以来,很多人认为黄金分割数是一个很特别的数. 一
些美术家认为: 如果人的上、下身长之比接近黄金分割数, 那
么可以增加美感. 据说,一些名画和雕塑中的人体大都符合这
个比,一位科学家曾提出: 在一棵树的生长过程中,??
? ? ? ?优选法是一种具有广泛应用价值的数学方法,著名数学家
华罗庚曾为普及它作出重要贡献. 优选法中有一种0.618法应用
了黄金分割数. 同学们可以查阅资料,了解0.618法的应用.
同课章节目录
