同底数幂的乘法
图片预览






文档简介
(共16张PPT)
15.1.1同底数幂的乘法
芜湖县实验学校
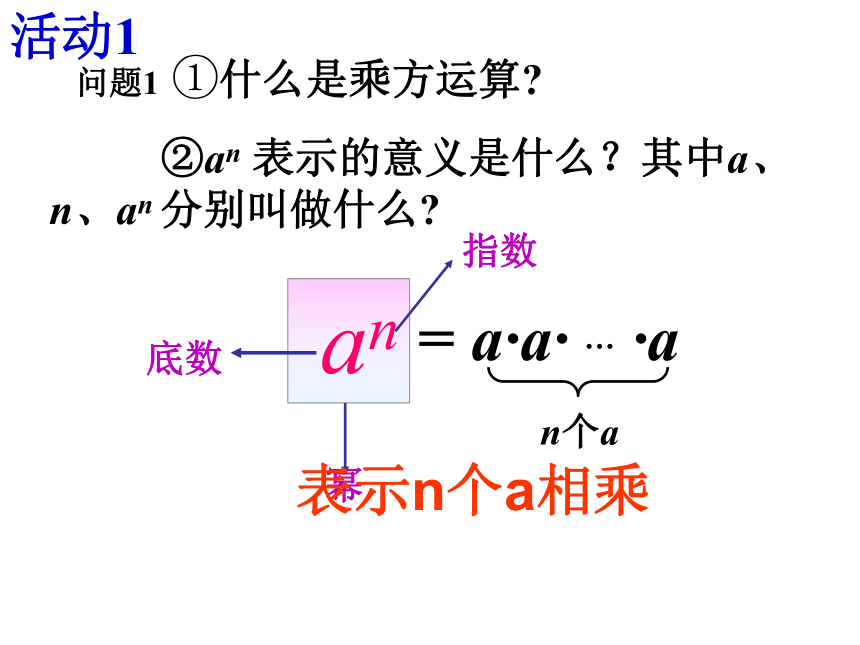
= a·a· … ·a
n个a
问题1 ①什么是乘方运算
②an 表示的意义是什么?其中a、n、an 分别叫做什么
an
底数
幂
指数
活动1
表示n个a相乘
问题2: 请你说出下列各幂的底数和指数
问题3: 一种电子计算机每秒可进行 次运算,
它工作 秒可进行多少次运算?
1014
103
①这是什么运算
②如何计算
=(10×···× 10 )×( 10×10×10 )
活动2
1014× 103
解:
14个10
=(10×10×···×10)
17个10
=1017
合作探究
1.计算
1014
×
103
25×22 = ( ) ×( )
= ________________ =2( ) ;
(2)a3×a2 = ( ) ×( )
=_______________= a( ) ;
(3) 5m · 5n =( ) ×( ) = 5( ).
2 × 2 ×2×2× 2
2 × 2
2×2 ×2 × 2×2×2×2
7
a×a×a
a×a
a×a×a×a×a
5
m+n
2.请同学们根据乘方的意义理解,完成下列填空.
5×···×5
m个5
n个5
5×···×5
(1)以上三个运算都是怎样的两数相乘?
① 25×22=27
② a3×a2=a5
③ 5m×5n=5m+n
思考:观察以下运算及其运算结果口答
(2)其运算结果有何规律?
(3)你能用数学语言来描述这一运算规律吗?
两个同底数的幂相乘
底数不变,指数相加
同底数的幂相乘,底数不变,指数相加
am · an =
m个a
n个a
= a·a…a
=am+n.
(m+n)个a
同底数幂相乘,底数不变,指数相加
即 am · an = am+n (m、n都是正整数)
(a·a…a)
(a·a…a)
同底数幂的乘法法则:
条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加
请同学们根据乘方的意义理解,完成下列填空.
例1 计算下列各式,结果用幂的形式表示.
(2) -a · a6 ;
21+4 +3
-(a1·a6)
xm+3m+1
(1) x2 · x5 ;
活动3
(4) xm · x3m+1 ;
x2+5
= x7
(3) 2× 24× 23 =
= 28
(2) -a · a6 =
= a1+6=a7
(3) 2× 24× 23 ;
(4) xm · x3m+1 =
= y4m+1
解(1) x2 · x5 =
a=a1
am· an· ap = am+n+p (m、n、p都是正整数)
练习:
(1)判断下面的计算是否正确
① ② ③ ④ ⑤
条件
①乘法
②同底数幂
结果
①底数不变
②指数相加
计算下列各式,结果用幂的形式表示.
(1) b5 × b ;
(2) 10× 102× 103 ;
(3) -a2 · a6 ;
(4) y2n · yn+1 ;
解:(1) b5 × b =
101+2 +3
- a2+6
y2n+n+1
b5+1
= b6
(2) 10× 102× 103 =
(3) -a2 · a6 =
= - a8
(4) y2n · yn+1 =
= y3n+1
= 106
练习2
练习3
解:
(1) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3 .
(1) (a-b)2 (a-b).
(3) (a-b)2(b-a)3
(3) (a-b)2(b-a)3
(2) (x+y) 3× (x+y).
(2) (x+y)3×(x+y)= (x+y) 3+1= (x+y)4 .
注:如果底数是互为相反的两个数,利用法则时,要把底数化成相同
=(b-a)2(b-a)3
=(b-a)2+3=(b-a)5
am+n= am · an (m、n都是正整数)
活动6
逆向应用、拓展创新
am· an=am+n
反过来
如:210=21+9=21×29
或 =22+8=22×28
例2
计算:
22009 - 22008
解:
22009 - 22008
= 21+2008 - 22008
= 2×22008 - 22008
= 22008
am · an =am+n(m,n都是正整数).
2.同底数幂的乘法性质:
1.幂的意义:
an = a·a· … ·a
n个a
am· an· ap = am+n+p (m、n、p都是正整数).
活动 小结:
3.逆向应用: am+n=am · an
作业
P148习题15.1
第1题(1)(2)
第2题(1)
15.1.1同底数幂的乘法
芜湖县实验学校
= a·a· … ·a
n个a
问题1 ①什么是乘方运算
②an 表示的意义是什么?其中a、n、an 分别叫做什么
an
底数
幂
指数
活动1
表示n个a相乘
问题2: 请你说出下列各幂的底数和指数
问题3: 一种电子计算机每秒可进行 次运算,
它工作 秒可进行多少次运算?
1014
103
①这是什么运算
②如何计算
=(10×···× 10 )×( 10×10×10 )
活动2
1014× 103
解:
14个10
=(10×10×···×10)
17个10
=1017
合作探究
1.计算
1014
×
103
25×22 = ( ) ×( )
= ________________ =2( ) ;
(2)a3×a2 = ( ) ×( )
=_______________= a( ) ;
(3) 5m · 5n =( ) ×( ) = 5( ).
2 × 2 ×2×2× 2
2 × 2
2×2 ×2 × 2×2×2×2
7
a×a×a
a×a
a×a×a×a×a
5
m+n
2.请同学们根据乘方的意义理解,完成下列填空.
5×···×5
m个5
n个5
5×···×5
(1)以上三个运算都是怎样的两数相乘?
① 25×22=27
② a3×a2=a5
③ 5m×5n=5m+n
思考:观察以下运算及其运算结果口答
(2)其运算结果有何规律?
(3)你能用数学语言来描述这一运算规律吗?
两个同底数的幂相乘
底数不变,指数相加
同底数的幂相乘,底数不变,指数相加
am · an =
m个a
n个a
= a·a…a
=am+n.
(m+n)个a
同底数幂相乘,底数不变,指数相加
即 am · an = am+n (m、n都是正整数)
(a·a…a)
(a·a…a)
同底数幂的乘法法则:
条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加
请同学们根据乘方的意义理解,完成下列填空.
例1 计算下列各式,结果用幂的形式表示.
(2) -a · a6 ;
21+4 +3
-(a1·a6)
xm+3m+1
(1) x2 · x5 ;
活动3
(4) xm · x3m+1 ;
x2+5
= x7
(3) 2× 24× 23 =
= 28
(2) -a · a6 =
= a1+6=a7
(3) 2× 24× 23 ;
(4) xm · x3m+1 =
= y4m+1
解(1) x2 · x5 =
a=a1
am· an· ap = am+n+p (m、n、p都是正整数)
练习:
(1)判断下面的计算是否正确
① ② ③ ④ ⑤
条件
①乘法
②同底数幂
结果
①底数不变
②指数相加
计算下列各式,结果用幂的形式表示.
(1) b5 × b ;
(2) 10× 102× 103 ;
(3) -a2 · a6 ;
(4) y2n · yn+1 ;
解:(1) b5 × b =
101+2 +3
- a2+6
y2n+n+1
b5+1
= b6
(2) 10× 102× 103 =
(3) -a2 · a6 =
= - a8
(4) y2n · yn+1 =
= y3n+1
= 106
练习2
练习3
解:
(1) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3 .
(1) (a-b)2 (a-b).
(3) (a-b)2(b-a)3
(3) (a-b)2(b-a)3
(2) (x+y) 3× (x+y).
(2) (x+y)3×(x+y)= (x+y) 3+1= (x+y)4 .
注:如果底数是互为相反的两个数,利用法则时,要把底数化成相同
=(b-a)2(b-a)3
=(b-a)2+3=(b-a)5
am+n= am · an (m、n都是正整数)
活动6
逆向应用、拓展创新
am· an=am+n
反过来
如:210=21+9=21×29
或 =22+8=22×28
例2
计算:
22009 - 22008
解:
22009 - 22008
= 21+2008 - 22008
= 2×22008 - 22008
= 22008
am · an =am+n(m,n都是正整数).
2.同底数幂的乘法性质:
1.幂的意义:
an = a·a· … ·a
n个a
am· an· ap = am+n+p (m、n、p都是正整数).
活动 小结:
3.逆向应用: am+n=am · an
作业
P148习题15.1
第1题(1)(2)
第2题(1)
