完全平方公式
图片预览

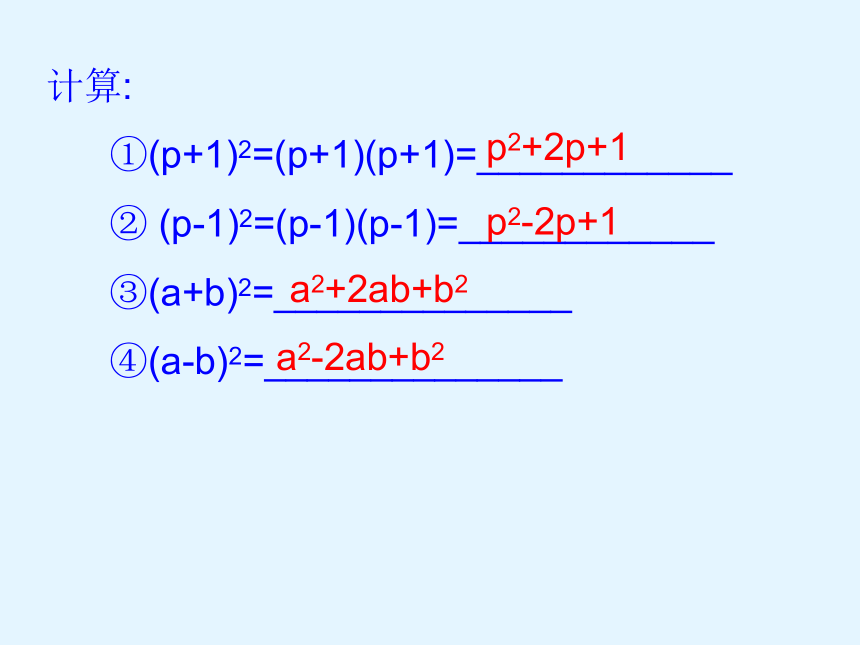




文档简介
(共15张PPT)
15.3.2 完全平方公式
计算:
①(p+1)2=(p+1)(p+1)=____________
② (p-1)2=(p-1)(p-1)=____________
③(a+b)2=______________
④(a-b)2=______________
p2+2p+1
p2-2p+1
a2+2ab+b2
a2-2ab+b2
动脑筋
想一想
(a+b)2=___________
(a-b)2=___________
两数和(或差)的平方等于这两数的平方和加上(或减去)这两数积的2倍.
a2+2ab+b2
a2-2ab+b2
用语言表述为:
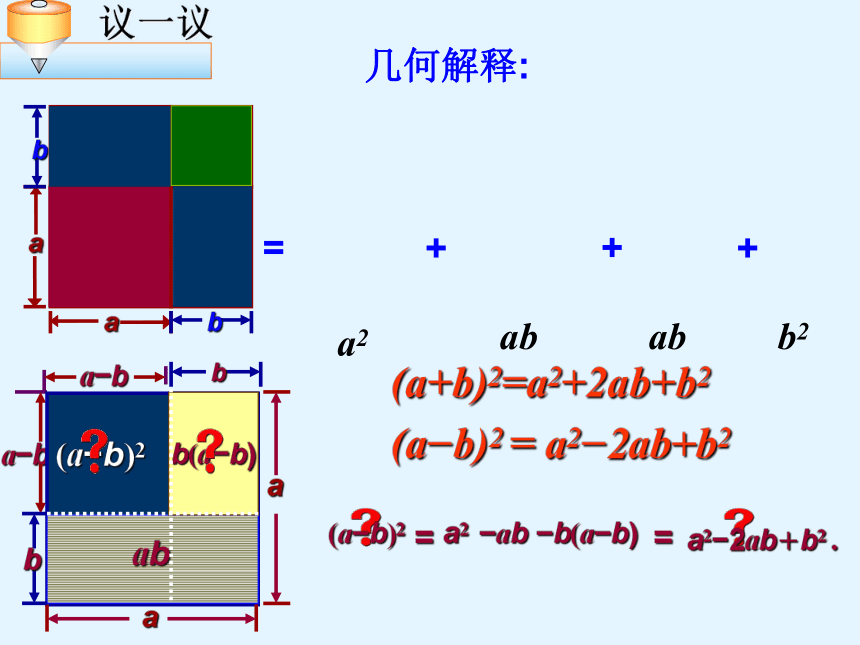
议一议
a
a
b
b
=
+
+
+
(a+b)2=a2+2ab+b2
几何解释:
a2
ab
b(a b)
=
a2 2ab+b2 .
=
(a b)2
a b
a b
a
a
ab
b(a b)
b
b
(a b)2
(a b)2 = a2 2ab+b2
a2
ab
ab
b2
初 识 完全平方公式
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
结构特征:
左边是
的平方;
二项式
右边是
a2 +b2
a2 +b2
(两数和 )
(差)
a+b
a b
两数的平方和
+
加上
(减去)
2ab
2ab
这两数乘积的两倍.
2
2
首平方,末平方,首末两倍中间放
比一比 赛一赛
回答下列问题:
(1) (a+2y)2是哪两个数的和的平方
(a+2y)2 =( ) 2+2( )( )+( ) 2
(2) (2x 5y)2是哪两个数的差的平方
(2x -5y)2 =( ) 2 -2( )( )+( ) 2
a
a
2y
2y
2x
2x
5y
5y
(2x 5y)2可以看成2x与 5y的和的平方.
(2x 5y)2可以看成哪两个数的和的平方
学一学
例1 利用完全平方公式计算:
(1) (4m+n)2 ; (2) (y-0.5x)2 ; (3) (-a b)2 ; (4) (b-a)2
解:(1) (4m+n)2=
4m
( )2
n
2
2×
4m
×n
+
+
(2) (y-0.5x)2=
=16m2+8mn+n2
y2-2×y×0.5x+(0.5x)2
=y2-xy+0.25x2
(3) (-a b)2=
(-a)2-2(-a)b+b2
=a2+2ab+b2
(4) (b-a)2=
b2-2 b a+a2
=b2-2ab+a2
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
(-a b)2=(a+b)2
(b a)2=(a-b)2
随堂练习
随堂练习
(1) (x +6)2 ; (2) (y -5)2;
(3) (-2x+5)2 ; (4) ( x - y)2
1、计算:
例题解析
学一学
例2 运用完全平方公式计算:
(1) 1022; (2) 992
解: (1) 1022 =
(100+2)2
变形
(2) 992=
=1002+2×100×2+22
=10000+400+4
=10404
(100-1)2=1002-2×100×1+12
=10000-200+1=9801
2、准确代入公式;
利用完全平方公式计算:
1 、先选择公式;
3、化简.
练习
计算
①192
②212
解:
192=(20-1)2
=202-2×20×1+1
=361
212=(20+1)2
=202+2×20×1+1
=441
下列等式是否成立 说明理由.
( 4a+1)2=(1 4a)2;
(2) ( 4a 1)2=(4a+1)2;
(3) (4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2;
(4) (4a 1)( 1 4a)=(4a 1)(4a+1).
成立
成立
不成立.
不成立.
一 判断题
(1)(-3x+4y)2=_____________.
(2)(-2a-b)2=____________.
(3)x2-4xy+________=(x-2y)2.
(4)a2+b2=(a+b)2+_________.
(5) a2+______+9b2=( a+3b)2
二 填空题
9x2-24xy+16y2
4a2+4ab+b2
4y2
(-2ab)
3ab
(1)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2
C.(36+12a)cm2 D.以上都不对
三 选择题
c
c
已知:
求: 和 的值
四 思考题
本节课你的收获是什么?
注意完全平方公式和平方差公式不同:
形式不同.
结果不同:
完全平方公式的结果 是三项,
即 (a b)2=a2 2ab+b2;
平方差公式的结果 是两项,
即 (a+b)(a b)=a2 b2.
有时需要进行变形,使变形后的式子符合应用完全平方公式
的条件,即为“两数和(或差)的平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键
15.3.2 完全平方公式
计算:
①(p+1)2=(p+1)(p+1)=____________
② (p-1)2=(p-1)(p-1)=____________
③(a+b)2=______________
④(a-b)2=______________
p2+2p+1
p2-2p+1
a2+2ab+b2
a2-2ab+b2
动脑筋
想一想
(a+b)2=___________
(a-b)2=___________
两数和(或差)的平方等于这两数的平方和加上(或减去)这两数积的2倍.
a2+2ab+b2
a2-2ab+b2
用语言表述为:
议一议
a
a
b
b
=
+
+
+
(a+b)2=a2+2ab+b2
几何解释:
a2
ab
b(a b)
=
a2 2ab+b2 .
=
(a b)2
a b
a b
a
a
ab
b(a b)
b
b
(a b)2
(a b)2 = a2 2ab+b2
a2
ab
ab
b2
初 识 完全平方公式
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
结构特征:
左边是
的平方;
二项式
右边是
a2 +b2
a2 +b2
(两数和 )
(差)
a+b
a b
两数的平方和
+
加上
(减去)
2ab
2ab
这两数乘积的两倍.
2
2
首平方,末平方,首末两倍中间放
比一比 赛一赛
回答下列问题:
(1) (a+2y)2是哪两个数的和的平方
(a+2y)2 =( ) 2+2( )( )+( ) 2
(2) (2x 5y)2是哪两个数的差的平方
(2x -5y)2 =( ) 2 -2( )( )+( ) 2
a
a
2y
2y
2x
2x
5y
5y
(2x 5y)2可以看成2x与 5y的和的平方.
(2x 5y)2可以看成哪两个数的和的平方
学一学
例1 利用完全平方公式计算:
(1) (4m+n)2 ; (2) (y-0.5x)2 ; (3) (-a b)2 ; (4) (b-a)2
解:(1) (4m+n)2=
4m
( )2
n
2
2×
4m
×n
+
+
(2) (y-0.5x)2=
=16m2+8mn+n2
y2-2×y×0.5x+(0.5x)2
=y2-xy+0.25x2
(3) (-a b)2=
(-a)2-2(-a)b+b2
=a2+2ab+b2
(4) (b-a)2=
b2-2 b a+a2
=b2-2ab+a2
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
(-a b)2=(a+b)2
(b a)2=(a-b)2
随堂练习
随堂练习
(1) (x +6)2 ; (2) (y -5)2;
(3) (-2x+5)2 ; (4) ( x - y)2
1、计算:
例题解析
学一学
例2 运用完全平方公式计算:
(1) 1022; (2) 992
解: (1) 1022 =
(100+2)2
变形
(2) 992=
=1002+2×100×2+22
=10000+400+4
=10404
(100-1)2=1002-2×100×1+12
=10000-200+1=9801
2、准确代入公式;
利用完全平方公式计算:
1 、先选择公式;
3、化简.
练习
计算
①192
②212
解:
192=(20-1)2
=202-2×20×1+1
=361
212=(20+1)2
=202+2×20×1+1
=441
下列等式是否成立 说明理由.
( 4a+1)2=(1 4a)2;
(2) ( 4a 1)2=(4a+1)2;
(3) (4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2;
(4) (4a 1)( 1 4a)=(4a 1)(4a+1).
成立
成立
不成立.
不成立.
一 判断题
(1)(-3x+4y)2=_____________.
(2)(-2a-b)2=____________.
(3)x2-4xy+________=(x-2y)2.
(4)a2+b2=(a+b)2+_________.
(5) a2+______+9b2=( a+3b)2
二 填空题
9x2-24xy+16y2
4a2+4ab+b2
4y2
(-2ab)
3ab
(1)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2
C.(36+12a)cm2 D.以上都不对
三 选择题
c
c
已知:
求: 和 的值
四 思考题
本节课你的收获是什么?
注意完全平方公式和平方差公式不同:
形式不同.
结果不同:
完全平方公式的结果 是三项,
即 (a b)2=a2 2ab+b2;
平方差公式的结果 是两项,
即 (a+b)(a b)=a2 b2.
有时需要进行变形,使变形后的式子符合应用完全平方公式
的条件,即为“两数和(或差)的平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键
