河北省邯郸市2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 河北省邯郸市2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 787.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 18:51:39 | ||
图片预览




文档简介
邯郸市2020—2021学年第二学期期末质量检测
高一数学
注意事项:
1. 考试时间120分钟,总共150分.
2. 答卷前,考生务必将自己的姓名、班级和考场填写在答题卡上,并把条形码贴在答题卡上的指定位置.
3. 回答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
4. 考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知向量false,false,若false,则false( )
A. false B. false C. false D. false
2. 在正四面体false中,直线false与直线false所成的角的大小为( )
A. false B. false C. false D. false
3. 已知某人射击每次击中目标的概率都是0.5,现在用随机模拟的方法估计此人3次射击至少2次击中目标的概率:先由计算器产生0到9之间的整数值的随机数,指定0,1,2,3,4表示击中目标,5,6,7,8,9表示未击中目标.每3个随机数为一组,代表3次射击的结果.经随机模拟产生了20组随机数:
926 446 072 021 392 077 663 817 325 615
405 858 776 631 700 259 305 311 589 258
据此估计,其3次射击至少2次击中目标的概率约为( )
A. 0.45 B. 0.5 C. 0.55 D. 0.6
4. 设false,false为两个不同的平面,false,false为两条不同的直线,下列命题正确的是( )
A. 若false,false,则false B. 若false,false,false,则false
C. 若false,false,则false D. 若false,false,false,则false
5. 甲、乙两人独立地解决同一问题,甲解出此问题的概率是0.8,乙解出此问题的概率是0.6,那么至少有一人解出此问题的概率是( )
A. 0.98 B. 0.92 C. 0.9 D. 0.88
6. 在false中,角false,false,false所对应的边分别是false,false,false,若false,false,则false的面积为( )
A. false B. 1 C. false D. 2
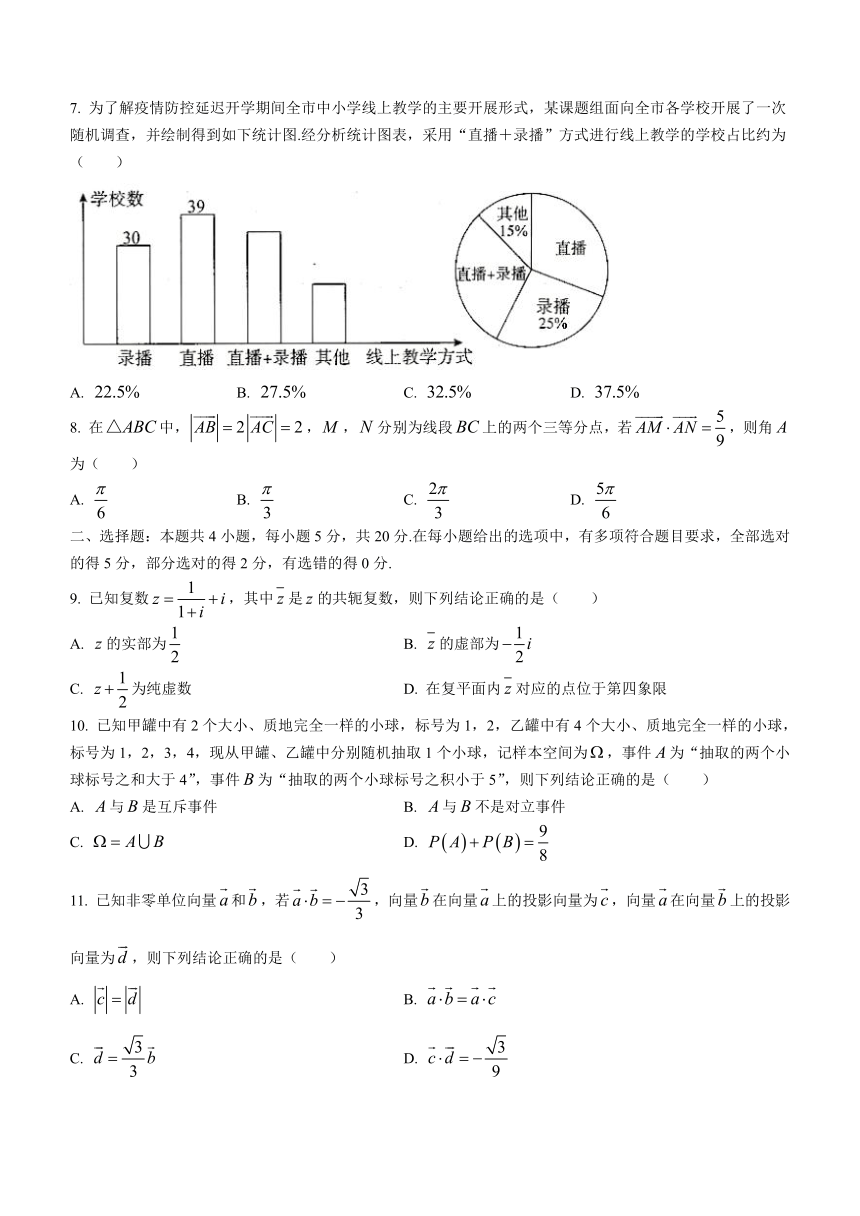
7. 为了解疫情防控延迟开学期间全市中小学线上教学的主要开展形式,某课题组面向全市各学校开展了一次随机调查,并绘制得到如下统计图.经分析统计图表,采用“直播+录播”方式进行线上教学的学校占比约为( )
A. false B. false C. false D. false
8. 在false中,false,false,false分别为线段false上的两个三等分点,若false,则角false为( )
A. false B. false C. false D. false
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知复数false,其中false是false的共轭复数,则下列结论正确的是( )
A. false的实部为false B. false的虚部为false
C. false为纯虚数 D. 在复平面内false对应的点位于第四象限
10. 已知甲罐中有2个大小、质地完全一样的小球,标号为1,2,乙罐中有4个大小、质地完全一样的小球,标号为1,2,3,4,现从甲罐、乙罐中分别随机抽取1个小球,记样本空间为false,事件false为“抽取的两个小球标号之和大于4”,事件false为“抽取的两个小球标号之积小于5”,则下列结论正确的是( )
A. false与false是互斥事件 B. false与false不是对立事件
C. false D. false
11. 已知非零单位向量false和false,若false,向量false在向量false上的投影向量为false,向量false在向量false上的投影向量为false,则下列结论正确的是( )
A. false B. false
C. false D. false
12. 已知正方体false的棱长为2,点false为false的中点,若以false为球心,false为半径的球面与正方体false的棱有四个交点false,false,false,false,则下列结论正确的是( )
A. 平面false平面false B. 平面false平面false
C. 四边形false的面积为false D. 四棱锥false的体积为false
三、填空题:本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.
13. 已知复数false,则false__________.
14. 将边长为2的正方形,绕其一条对角线旋转false,所围成的几何体的表面积为__________.
15. 已知正方体false,则二面角false的正弦值为___________.
16. 在false中,角false,false,false所对应的边分别是false,false,false,已知false,且false为钝角,则false______________,false的取值范围是___________.
四、解答题:本题共6小题,第17题10分,第18~22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在false中,角false,false,false所对应的边分别是false,false,false,且false.
(1)求角false的大小;
(2)若false,在下面三个条件中选一个,若false存在,求false的值,若不存在,说明理由.
①false;②false;③false.
注:如果选择多个条件分别解答,按第一个解答计分.
18. 如图,已知false为平面直角坐标系的原点,false,false.
(1)求false的坐标;
(2)若四边形false为平行四边形,求false.
19. 如图,在三棱锥false中,false,false,false,false平面false.
(1)求证:平面false平面false;
(2)若false,false是false的中点,求false与平面false所成角的正切值.
20. 甲、乙两人玩一个掷骰子游戏,规则如下:甲掷两次骰子,第一次掷出的数字作为十位数,第二次掷出的数字作为个位数,组成一个两位数,然后让乙猜.若乙猜出的结果与该两位数满足的数字特征相符,则乙获胜,否则甲获胜,一轮游戏结束,然后进行下一轮(每轮游戏都由甲掷两次骰子).
所要猜的两位数的数字特征方案从以下两种猜法中选择一种;
猜法一:猜“两位数的十位大于个位”;
猜法二:猜“两位数的十位不大于个位”.
请回答:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜法,并说明理由;
(2)假定每轮游戏结果相互独立,规定有人连续获胜两次则整个游戏停止.若乙按照(1)中的猜法进行游戏,求第三轮后游戏停止的概率.
21. 如图,在直三棱柱false中,false是边长为2的正三角形,点false,false分别是棱false,false上的点,点false是线段false上一点,false.
(1)若false为中点,证明:false平面false;
(2)若false,求false.
22. 某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有false人,按年龄分成5组,其中第一组:false,第二组:false,第三组:false,第四组:false,第五组:false,得到如图所示的频率分布直方图,已知第一组有10人.
(1)根据频率分布直方图,估计这false人的平均年龄和第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任本市的“中国梦”宣传使者.
(i)若有甲(年龄38),乙(年龄40)两人已确定人选宣传使者,现计划从第四组和第五组被抽到的使者中,再随机抽取2名作为组长,求甲、乙两人至少有一人被选上的概率;
(ii)若第四组宣传使者的年龄的平均数与方差分别为37和false,第五组宣传使者的年龄的平均数与方差分别为43和1,据此估计这false人中35~45岁所有人的年龄的方差.
高一数学参考答案
一、选择题
1-5:ADBCB 6-8:ABC
二、选择题
9. AD 10. BCD 11. ABD 12. ACD
三、填空题
13. 1 14. false 15. false 16. false false
四、解答题
17. 解:(1)因为false,
由正弦定理,得false,
即false,
又因为false,
所以false,
又因为false,
所以false,
从而false,故false.
(2)显然有false,若false存在,必有false.
选①false:此时有false,故false不存在.
选②false:此时有false,如图1,false存在,且false有唯一解.故有false.
选③false:此时有false,如图2,false存在,且false有两解(false与false).
由余弦定理,得false,即false,解得false或false.
18. 解:(1)如图1所示,过点false作false轴,false轴,false,false、false分别为垂足.
显然,false,false.
故false,false.
所以false,从而false.
(2)方法1:如图2所示,设false,
由平行四边形法则,false,
由于false,所以false.
方法2:由(1)知,false.
由于四边形false为平行四边形,所以false,
设点false,则false.
又false,故false,解得false,即false.
所以false,从而false.
方法3:如图2所示,设false,则false为false和false的中点.
由(1)知,false,false,false.
设点false,则false,
又false,故false,
故false,从而false.
19. 解:(1)证明:在false中,false,false,false,
由余弦定理得false.
所以false,从而false,
由勾股定理得,false.
又因为false平面false,false平面false,
所以false,
由于false平面false,false平面false,false,
所以false平面false,
又因为false平面false,
所以平面false平面false.
(2)取false中点false,连接false,false.
因为false,所以false.
又因为平面false平面false,平面false平面false,
所以false平面false,
故false即为直线false与平面false所成的角,
因为false,false,
所以false,false,所以false,
则false,
所以false与平面false所成角的正切值为false.
20. 解:(1)两个骰子掷出的数字所构成的两位数组成样本空间:
false
false,
共36个样本点.
设事件false为“两位数的十位大于个位”,false为“两位数的十位不大于个位”,
则false,false.
为了尽可能获胜,应该选择猜法二.
(2)设事件false为“游戏结束时甲连续获胜两次”,false为“游戏结束时乙连续获胜两次”.
则false,false.
故第三轮后游戏停止的概率为
false.
21. 解:(1)证明:取false中点false,连接false,false,
则false且false,
又因为false且false,
所以false,且false,
所以四边形false为平行四边形,
从而false.
又false平面false,false平面false,
所以false平面false.
(2)作false交false于false,则false为false中点.
所以false平面false,
因为false是边长为2的正三角形,且false.
所以false.
则false,
所以false.
又因为false,所以false.
22. 解:(1)设这false人的平均年龄为false,则
false(岁).
设第80百分位数为false,
方法一:由false,解得false.
方法二:由false,解得false.
(2)(i)由题意得,第四组应抽取4人,记为false,false,false,甲,第五组抽取2人,记为false,乙.
对应的样本空间为:
false
false,共15个样本点.
设事件false“甲、乙两人至少一人被选上”,则
false,共有9个样本点.
所以,false.
(ii)设第四组、第五组的宣传使者的年龄的平均数分别为false,false,方差分别为false,false,
则false,false,false,false,
设第四组和第五组所有宣传使者的年龄平均数为false,方差为false.
则false,
false.
因此,第四组和第五组所有宣传使者的年龄方差为10.
据此,可估计这false人中年龄在35~45岁的所有人的年龄方差约为10.
高一数学
注意事项:
1. 考试时间120分钟,总共150分.
2. 答卷前,考生务必将自己的姓名、班级和考场填写在答题卡上,并把条形码贴在答题卡上的指定位置.
3. 回答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
4. 考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知向量false,false,若false,则false( )
A. false B. false C. false D. false
2. 在正四面体false中,直线false与直线false所成的角的大小为( )
A. false B. false C. false D. false
3. 已知某人射击每次击中目标的概率都是0.5,现在用随机模拟的方法估计此人3次射击至少2次击中目标的概率:先由计算器产生0到9之间的整数值的随机数,指定0,1,2,3,4表示击中目标,5,6,7,8,9表示未击中目标.每3个随机数为一组,代表3次射击的结果.经随机模拟产生了20组随机数:
926 446 072 021 392 077 663 817 325 615
405 858 776 631 700 259 305 311 589 258
据此估计,其3次射击至少2次击中目标的概率约为( )
A. 0.45 B. 0.5 C. 0.55 D. 0.6
4. 设false,false为两个不同的平面,false,false为两条不同的直线,下列命题正确的是( )
A. 若false,false,则false B. 若false,false,false,则false
C. 若false,false,则false D. 若false,false,false,则false
5. 甲、乙两人独立地解决同一问题,甲解出此问题的概率是0.8,乙解出此问题的概率是0.6,那么至少有一人解出此问题的概率是( )
A. 0.98 B. 0.92 C. 0.9 D. 0.88
6. 在false中,角false,false,false所对应的边分别是false,false,false,若false,false,则false的面积为( )
A. false B. 1 C. false D. 2
7. 为了解疫情防控延迟开学期间全市中小学线上教学的主要开展形式,某课题组面向全市各学校开展了一次随机调查,并绘制得到如下统计图.经分析统计图表,采用“直播+录播”方式进行线上教学的学校占比约为( )
A. false B. false C. false D. false
8. 在false中,false,false,false分别为线段false上的两个三等分点,若false,则角false为( )
A. false B. false C. false D. false
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知复数false,其中false是false的共轭复数,则下列结论正确的是( )
A. false的实部为false B. false的虚部为false
C. false为纯虚数 D. 在复平面内false对应的点位于第四象限
10. 已知甲罐中有2个大小、质地完全一样的小球,标号为1,2,乙罐中有4个大小、质地完全一样的小球,标号为1,2,3,4,现从甲罐、乙罐中分别随机抽取1个小球,记样本空间为false,事件false为“抽取的两个小球标号之和大于4”,事件false为“抽取的两个小球标号之积小于5”,则下列结论正确的是( )
A. false与false是互斥事件 B. false与false不是对立事件
C. false D. false
11. 已知非零单位向量false和false,若false,向量false在向量false上的投影向量为false,向量false在向量false上的投影向量为false,则下列结论正确的是( )
A. false B. false
C. false D. false
12. 已知正方体false的棱长为2,点false为false的中点,若以false为球心,false为半径的球面与正方体false的棱有四个交点false,false,false,false,则下列结论正确的是( )
A. 平面false平面false B. 平面false平面false
C. 四边形false的面积为false D. 四棱锥false的体积为false
三、填空题:本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.
13. 已知复数false,则false__________.
14. 将边长为2的正方形,绕其一条对角线旋转false,所围成的几何体的表面积为__________.
15. 已知正方体false,则二面角false的正弦值为___________.
16. 在false中,角false,false,false所对应的边分别是false,false,false,已知false,且false为钝角,则false______________,false的取值范围是___________.
四、解答题:本题共6小题,第17题10分,第18~22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在false中,角false,false,false所对应的边分别是false,false,false,且false.
(1)求角false的大小;
(2)若false,在下面三个条件中选一个,若false存在,求false的值,若不存在,说明理由.
①false;②false;③false.
注:如果选择多个条件分别解答,按第一个解答计分.
18. 如图,已知false为平面直角坐标系的原点,false,false.
(1)求false的坐标;
(2)若四边形false为平行四边形,求false.
19. 如图,在三棱锥false中,false,false,false,false平面false.
(1)求证:平面false平面false;
(2)若false,false是false的中点,求false与平面false所成角的正切值.
20. 甲、乙两人玩一个掷骰子游戏,规则如下:甲掷两次骰子,第一次掷出的数字作为十位数,第二次掷出的数字作为个位数,组成一个两位数,然后让乙猜.若乙猜出的结果与该两位数满足的数字特征相符,则乙获胜,否则甲获胜,一轮游戏结束,然后进行下一轮(每轮游戏都由甲掷两次骰子).
所要猜的两位数的数字特征方案从以下两种猜法中选择一种;
猜法一:猜“两位数的十位大于个位”;
猜法二:猜“两位数的十位不大于个位”.
请回答:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜法,并说明理由;
(2)假定每轮游戏结果相互独立,规定有人连续获胜两次则整个游戏停止.若乙按照(1)中的猜法进行游戏,求第三轮后游戏停止的概率.
21. 如图,在直三棱柱false中,false是边长为2的正三角形,点false,false分别是棱false,false上的点,点false是线段false上一点,false.
(1)若false为中点,证明:false平面false;
(2)若false,求false.
22. 某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有false人,按年龄分成5组,其中第一组:false,第二组:false,第三组:false,第四组:false,第五组:false,得到如图所示的频率分布直方图,已知第一组有10人.
(1)根据频率分布直方图,估计这false人的平均年龄和第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任本市的“中国梦”宣传使者.
(i)若有甲(年龄38),乙(年龄40)两人已确定人选宣传使者,现计划从第四组和第五组被抽到的使者中,再随机抽取2名作为组长,求甲、乙两人至少有一人被选上的概率;
(ii)若第四组宣传使者的年龄的平均数与方差分别为37和false,第五组宣传使者的年龄的平均数与方差分别为43和1,据此估计这false人中35~45岁所有人的年龄的方差.
高一数学参考答案
一、选择题
1-5:ADBCB 6-8:ABC
二、选择题
9. AD 10. BCD 11. ABD 12. ACD
三、填空题
13. 1 14. false 15. false 16. false false
四、解答题
17. 解:(1)因为false,
由正弦定理,得false,
即false,
又因为false,
所以false,
又因为false,
所以false,
从而false,故false.
(2)显然有false,若false存在,必有false.
选①false:此时有false,故false不存在.
选②false:此时有false,如图1,false存在,且false有唯一解.故有false.
选③false:此时有false,如图2,false存在,且false有两解(false与false).
由余弦定理,得false,即false,解得false或false.
18. 解:(1)如图1所示,过点false作false轴,false轴,false,false、false分别为垂足.
显然,false,false.
故false,false.
所以false,从而false.
(2)方法1:如图2所示,设false,
由平行四边形法则,false,
由于false,所以false.
方法2:由(1)知,false.
由于四边形false为平行四边形,所以false,
设点false,则false.
又false,故false,解得false,即false.
所以false,从而false.
方法3:如图2所示,设false,则false为false和false的中点.
由(1)知,false,false,false.
设点false,则false,
又false,故false,
故false,从而false.
19. 解:(1)证明:在false中,false,false,false,
由余弦定理得false.
所以false,从而false,
由勾股定理得,false.
又因为false平面false,false平面false,
所以false,
由于false平面false,false平面false,false,
所以false平面false,
又因为false平面false,
所以平面false平面false.
(2)取false中点false,连接false,false.
因为false,所以false.
又因为平面false平面false,平面false平面false,
所以false平面false,
故false即为直线false与平面false所成的角,
因为false,false,
所以false,false,所以false,
则false,
所以false与平面false所成角的正切值为false.
20. 解:(1)两个骰子掷出的数字所构成的两位数组成样本空间:
false
false,
共36个样本点.
设事件false为“两位数的十位大于个位”,false为“两位数的十位不大于个位”,
则false,false.
为了尽可能获胜,应该选择猜法二.
(2)设事件false为“游戏结束时甲连续获胜两次”,false为“游戏结束时乙连续获胜两次”.
则false,false.
故第三轮后游戏停止的概率为
false.
21. 解:(1)证明:取false中点false,连接false,false,
则false且false,
又因为false且false,
所以false,且false,
所以四边形false为平行四边形,
从而false.
又false平面false,false平面false,
所以false平面false.
(2)作false交false于false,则false为false中点.
所以false平面false,
因为false是边长为2的正三角形,且false.
所以false.
则false,
所以false.
又因为false,所以false.
22. 解:(1)设这false人的平均年龄为false,则
false(岁).
设第80百分位数为false,
方法一:由false,解得false.
方法二:由false,解得false.
(2)(i)由题意得,第四组应抽取4人,记为false,false,false,甲,第五组抽取2人,记为false,乙.
对应的样本空间为:
false
false,共15个样本点.
设事件false“甲、乙两人至少一人被选上”,则
false,共有9个样本点.
所以,false.
(ii)设第四组、第五组的宣传使者的年龄的平均数分别为false,false,方差分别为false,false,
则false,false,false,false,
设第四组和第五组所有宣传使者的年龄平均数为false,方差为false.
则false,
false.
因此,第四组和第五组所有宣传使者的年龄方差为10.
据此,可估计这false人中年龄在35~45岁的所有人的年龄方差约为10.
同课章节目录
