浙江省宁波万里国际学校2012届高三上学期期中考试数学(文)试题
文档属性
| 名称 | 浙江省宁波万里国际学校2012届高三上学期期中考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 483.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-08 14:53:25 | ||
图片预览




文档简介
高三年级 文科数学试题卷
答卷时间:120分钟 满分:150 命题人:舒毓维 校对人:舒毓维
一、选择题(本大题共10小题,每小题5分,共50分)
1. 设全集,集合,则
A. B.(0,1) C. D.
2.函数零点的个数是
A. 0 B.1 C.2 D.3
3.下列说法正确的是
A.异面直线所成的角范围是
B.命题“”的否定是“”
C.若为假命题,则,均为假命题
D.成立的充分而不必要的条件是
4.对于平面、、和直线、、m、n,下列命题中真命题是
A.若,则 B.若,则
C.若,则 D.若则
5.下列结论中正确的是
A.将的图象向右平移得到的图象
B.的一条对称轴是
C.若,则
D.的一个对称中心是
6.如图在平行四边形中,已知,,,为的中点,则
A. B. C. D.
7.执行下面的程序框图,若,则输出的等于
. . . .
8.过点的直线交圆于两点,
且,则直线的方程为
A. B. C. D.
9. 已知双曲线的一条渐近线方程是,它的一个焦点在抛物线的准线上,则双曲线的方程为
A. B. C. D.
10. 设、满足约束条件 ,若目标函数的最大值为6,则的最小值为
A.2 B.3 C. D.4
二、填空题(本大题共7小题,每小题4分,共28分)
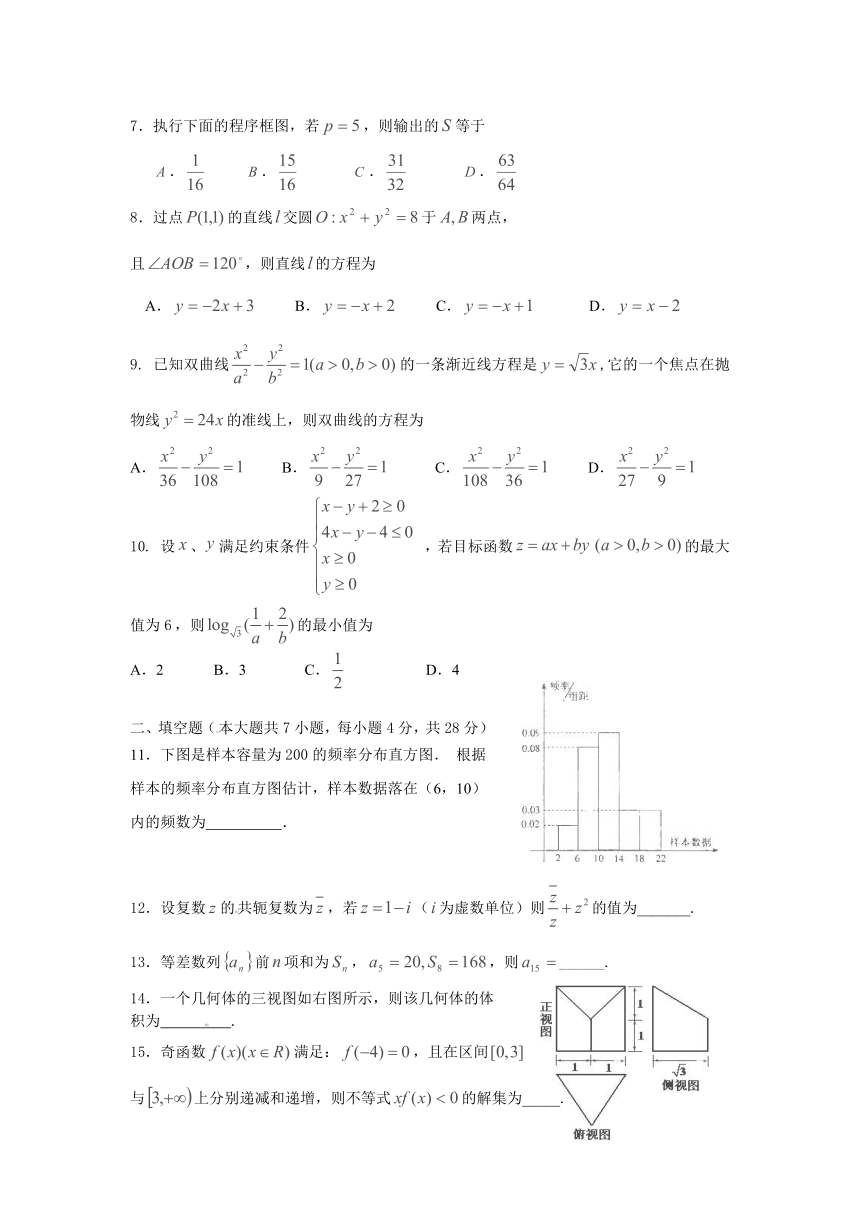
11.下图是样本容量为200的频率分布直方图. 根据样本的频率分布直方图估计,样本数据落在(6,10)内的频数为 .
12.设复数的共轭复数为,若(为虚数单位)则的值为_______.
13.等差数列前项和为,,则______.
14.一个几何体的三视图如右图所示,则该几何体的体
积为 .
15.奇函数满足:,且在区间
与上分别递减和递增,则不等式的解集为_____.
16.在中,角所对的边分别为,
且,则 .
17.如图,已知点是正四面体的棱中点,则
直线与平面所成角的正弦值为__________.
三、解答题(本大题共5小题,共69分)
18.(本题满分13分)已知向量 ,,函数. ( http: / / www. )
(Ⅰ)求的单调增区间;
(Ⅱ)若在中,角 HYPERLINK "http://www." 所对的边分别是,且满足:
,求的取值范围.
19.(本题满分14分)已知数列的前项和为,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)若数列的前项和为,求数列的通项公式.
20.(本题满分14分)如图,在四棱锥中,⊥底面,底面为正方形,,、分别是、的中点.
(Ⅰ)求证:∥面;
(Ⅱ)求异面直线与所成角的大小;
(Ⅲ)在上是否存在点,使⊥面,给出理由或证明.
21.(本小题满分14分)已知,函数,(其中为自然对数的底数).
(Ⅰ)判断函数在上的单调性;
(II)是否存在实数,使曲线在点处的切线与轴垂直 若存在,
求出的值;若不存在,请说明理由;
22.(本题满分14分)已知直线:与抛物线相交于不同的两点,直线分别是抛物线在点、处的切线,∩;若分别交x轴于、两点,且.
(Ⅰ)记点的横坐标分别为,试求出满足的关系式;
(Ⅱ)求证:△MNP的面积是定值,并求出这个定值.
宁波万里国际学校中学
2011-2012学年度第一学期期中考试
高三年级 文科数学答题卷
一、选择一、选择题:(本大题共10小题,每小题5分,共50分)
题 号 1 2 3 4 5 6 7 8 9 10 得 分
答 案
二、填空题:(本大题共7小题,每小题4分,共28分)
11._____________________;12.__________________;13.____________________
14.____________;15._______________;16.____________;17.________________
三、解答题:(本大题共5小题,共69分)
18.(本小题满分13分)
19. (本小题满分14分)20. (本小题满分14分)
21. (本小题满分14分)
22. (本小题满分14分)
2011-2012学年度第一学期期中考试
高三文科数学参考答案
(Ⅱ)由正弦定理得: HYPERLINK "http://www." ,
即 ……8分
由 得: HYPERLINK "http://www." ,又……10分
又得:,
HYPERLINK "http://www." ,
, ……12分
∴的取值范围是 ……13分
19、解:(Ⅰ),当时,,,
∴ 时, ∴数列是首项为,公比为的等比数列,
,……………………………………………………………7分
(Ⅱ)由(Ⅰ)知,
∴
∴
∴ ……………………………………………………………14分
21、解:((1)∵,,∴. ……1分
①若,则,在上单调递增; ……3分
②若,当时,,函数在区间上单调递减,
当时,,函数在区间上单调递增, ……5分
③若,则,函数在区间上单调递减. ……………………7分
(2)解:∵,,
, ……8分
由(1)易知,当时,在上的最小值:,即时,. ………………………10分
又,∴. ……12分
曲线在点处的切线与轴垂直等价于方程有实数解.
而,即方程无实数解.故不存在. ………………………14分
22、解:(1)设
切线方程分别为:, …………3分
则
因为,所以有, …………6分
(2)设,由,解得……(1) …………8分
联立消去,得
所以……(2) …………10分
A
B
C
D
P
座位号
答卷时间:120分钟 满分:150 命题人:舒毓维 校对人:舒毓维
一、选择题(本大题共10小题,每小题5分,共50分)
1. 设全集,集合,则
A. B.(0,1) C. D.
2.函数零点的个数是
A. 0 B.1 C.2 D.3
3.下列说法正确的是
A.异面直线所成的角范围是
B.命题“”的否定是“”
C.若为假命题,则,均为假命题
D.成立的充分而不必要的条件是
4.对于平面、、和直线、、m、n,下列命题中真命题是
A.若,则 B.若,则
C.若,则 D.若则
5.下列结论中正确的是
A.将的图象向右平移得到的图象
B.的一条对称轴是
C.若,则
D.的一个对称中心是
6.如图在平行四边形中,已知,,,为的中点,则
A. B. C. D.
7.执行下面的程序框图,若,则输出的等于
. . . .
8.过点的直线交圆于两点,
且,则直线的方程为
A. B. C. D.
9. 已知双曲线的一条渐近线方程是,它的一个焦点在抛物线的准线上,则双曲线的方程为
A. B. C. D.
10. 设、满足约束条件 ,若目标函数的最大值为6,则的最小值为
A.2 B.3 C. D.4
二、填空题(本大题共7小题,每小题4分,共28分)
11.下图是样本容量为200的频率分布直方图. 根据样本的频率分布直方图估计,样本数据落在(6,10)内的频数为 .
12.设复数的共轭复数为,若(为虚数单位)则的值为_______.
13.等差数列前项和为,,则______.
14.一个几何体的三视图如右图所示,则该几何体的体
积为 .
15.奇函数满足:,且在区间
与上分别递减和递增,则不等式的解集为_____.
16.在中,角所对的边分别为,
且,则 .
17.如图,已知点是正四面体的棱中点,则
直线与平面所成角的正弦值为__________.
三、解答题(本大题共5小题,共69分)
18.(本题满分13分)已知向量 ,,函数. ( http: / / www. )
(Ⅰ)求的单调增区间;
(Ⅱ)若在中,角 HYPERLINK "http://www." 所对的边分别是,且满足:
,求的取值范围.
19.(本题满分14分)已知数列的前项和为,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)若数列的前项和为,求数列的通项公式.
20.(本题满分14分)如图,在四棱锥中,⊥底面,底面为正方形,,、分别是、的中点.
(Ⅰ)求证:∥面;
(Ⅱ)求异面直线与所成角的大小;
(Ⅲ)在上是否存在点,使⊥面,给出理由或证明.
21.(本小题满分14分)已知,函数,(其中为自然对数的底数).
(Ⅰ)判断函数在上的单调性;
(II)是否存在实数,使曲线在点处的切线与轴垂直 若存在,
求出的值;若不存在,请说明理由;
22.(本题满分14分)已知直线:与抛物线相交于不同的两点,直线分别是抛物线在点、处的切线,∩;若分别交x轴于、两点,且.
(Ⅰ)记点的横坐标分别为,试求出满足的关系式;
(Ⅱ)求证:△MNP的面积是定值,并求出这个定值.
宁波万里国际学校中学
2011-2012学年度第一学期期中考试
高三年级 文科数学答题卷
一、选择一、选择题:(本大题共10小题,每小题5分,共50分)
题 号 1 2 3 4 5 6 7 8 9 10 得 分
答 案
二、填空题:(本大题共7小题,每小题4分,共28分)
11._____________________;12.__________________;13.____________________
14.____________;15._______________;16.____________;17.________________
三、解答题:(本大题共5小题,共69分)
18.(本小题满分13分)
19. (本小题满分14分)20. (本小题满分14分)
21. (本小题满分14分)
22. (本小题满分14分)
2011-2012学年度第一学期期中考试
高三文科数学参考答案
(Ⅱ)由正弦定理得: HYPERLINK "http://www." ,
即 ……8分
由 得: HYPERLINK "http://www." ,又……10分
又得:,
HYPERLINK "http://www." ,
, ……12分
∴的取值范围是 ……13分
19、解:(Ⅰ),当时,,,
∴ 时, ∴数列是首项为,公比为的等比数列,
,……………………………………………………………7分
(Ⅱ)由(Ⅰ)知,
∴
∴
∴ ……………………………………………………………14分
21、解:((1)∵,,∴. ……1分
①若,则,在上单调递增; ……3分
②若,当时,,函数在区间上单调递减,
当时,,函数在区间上单调递增, ……5分
③若,则,函数在区间上单调递减. ……………………7分
(2)解:∵,,
, ……8分
由(1)易知,当时,在上的最小值:,即时,. ………………………10分
又,∴. ……12分
曲线在点处的切线与轴垂直等价于方程有实数解.
而,即方程无实数解.故不存在. ………………………14分
22、解:(1)设
切线方程分别为:, …………3分
则
因为,所以有, …………6分
(2)设,由,解得……(1) …………8分
联立消去,得
所以……(2) …………10分
A
B
C
D
P
座位号
同课章节目录
