四川省攀枝花市米易中学2012届高三9月月考数学(理)试题(无答案)
文档属性
| 名称 | 四川省攀枝花市米易中学2012届高三9月月考数学(理)试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 108.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-08 16:27:37 | ||
图片预览

文档简介
一、选择题(本大题共12小题,每小题5分)
1.设集合,( )
A. B. C. D.
2、y=(1≤x≤2)的反函数是 ( )
A.y=1+(-1≤x≤1)
B.y=1+ (0≤x≤1)
C.y=1- (-1≤x≤1)
D.y=1- (0≤x≤1)
3、关于x的不等式ax-b>0的解集是(1,+ ∞),则关于x的不等式的解集是( )
A.(-∞,-1)∪(2,+ ∞) B.(-1,2) C.(1,2) D(-∞,1) ∪(2,+ ∞)
4、设正数a,b满足, 则( )
A.0 B. C. D.1
5、下列有关命题的说法正确的是 ( )
A.命题“若”的否命题为:“若”
B.“x=-1”是“”的必要不充分条件
C.命题“”的否定是:“”
D.命题“若”的逆否命题为真命题函数
6、从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为( )
A. B. C. D.
7、已知不等式|x-m|<1成立的充分非必要条件是,则实数m的取值范围是 ( )
A. B. C. D.
8、已知命题p:函数log0.5(x2+2x+a)的值域为R,命题q:函数y=-(5-2a)x是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
A.a≤1 B.a<2 C.19、关于函数有下列三个结论:①的值域为R;②是R上的增函数;③对任意成立;其中所有正确的序号为( )
A.①② B.①③ C.②③ D.①②③
10、若函数f(x)=loga(x3-ax)(a>0且a≠1)在区间(-,0)内单调递增,则a的取值范围是 ( )
A. [,1 ) B. [,1) C.[,+∞) D.(1,)
11、设是连续的偶函数,且当时是单调函数,则满足的所有之和为( )
A. B. C. D.
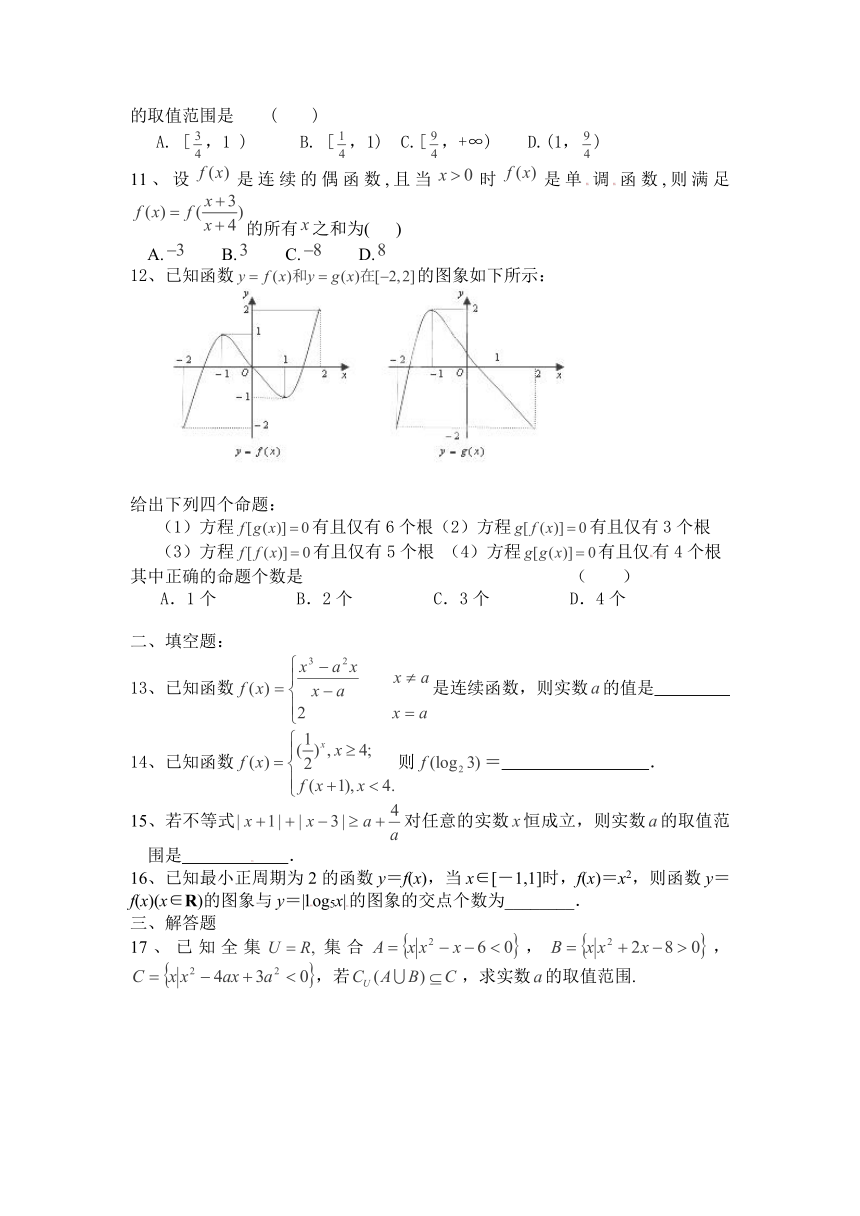
12、已知函数的图象如下所示:
给出下列四个命题:
(1)方程有且仅有6个根(2)方程有且仅有3个根
(3)方程有且仅有5个根 (4)方程有且仅有4个根
其中正确的命题个数是 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题:
13、已知函数是连续函数,则实数的值是
14、已知函数则= .
15、若不等式对任意的实数恒成立,则实数的取值范围是 .
16、已知最小正周期为2的函数y=f(x),当x∈[-1,1]时,f(x)=x2,则函数y=f(x)(x∈R)的图象与y=|log5x|的图象的交点个数为________.
三、解答题
17、已知全集集合,,,若,求实数的取值范围.
18、已知函数
f(x)
求函数f(x)的解析式;
(2) 设k>1,解关于x的不等式:
19、如图,四棱锥的底面为正方形,侧棱底面,且,分别是线段的中点.
(Ⅰ)求证://平面;(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
20、已知m∈R,设P:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立。
Q:函数f(x)=x3+(m+)x+6在(-∞,+ ∞)上有极值。
求使P正确且Q正确的m的取值范围。
21.已知二次函数f (x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c∈R,且满足a>b>c, f(1)=0.
(1)证明:函数f(x)与g(x)的图像交于不同的两点A、B;
(2)若函数F(x)=f(x)-g(x)在[2,3]上的最小值为9,最大值为21,试求a、b的值.
(3)求线段AB在x轴上的射影A1B1的长的取值范围.
22、已知函数(a为常数)是R上的奇函数,函数
是区间[-1,1]上的减函数.
(I)求a的值;
(II)若上恒成立,求t的取值范围;
(III)讨论关于x的方程的根的个数.
1.设集合,( )
A. B. C. D.
2、y=(1≤x≤2)的反函数是 ( )
A.y=1+(-1≤x≤1)
B.y=1+ (0≤x≤1)
C.y=1- (-1≤x≤1)
D.y=1- (0≤x≤1)
3、关于x的不等式ax-b>0的解集是(1,+ ∞),则关于x的不等式的解集是( )
A.(-∞,-1)∪(2,+ ∞) B.(-1,2) C.(1,2) D(-∞,1) ∪(2,+ ∞)
4、设正数a,b满足, 则( )
A.0 B. C. D.1
5、下列有关命题的说法正确的是 ( )
A.命题“若”的否命题为:“若”
B.“x=-1”是“”的必要不充分条件
C.命题“”的否定是:“”
D.命题“若”的逆否命题为真命题函数
6、从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为( )
A. B. C. D.
7、已知不等式|x-m|<1成立的充分非必要条件是,则实数m的取值范围是 ( )
A. B. C. D.
8、已知命题p:函数log0.5(x2+2x+a)的值域为R,命题q:函数y=-(5-2a)x是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
A.a≤1 B.a<2 C.1
A.①② B.①③ C.②③ D.①②③
10、若函数f(x)=loga(x3-ax)(a>0且a≠1)在区间(-,0)内单调递增,则a的取值范围是 ( )
A. [,1 ) B. [,1) C.[,+∞) D.(1,)
11、设是连续的偶函数,且当时是单调函数,则满足的所有之和为( )
A. B. C. D.
12、已知函数的图象如下所示:
给出下列四个命题:
(1)方程有且仅有6个根(2)方程有且仅有3个根
(3)方程有且仅有5个根 (4)方程有且仅有4个根
其中正确的命题个数是 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题:
13、已知函数是连续函数,则实数的值是
14、已知函数则= .
15、若不等式对任意的实数恒成立,则实数的取值范围是 .
16、已知最小正周期为2的函数y=f(x),当x∈[-1,1]时,f(x)=x2,则函数y=f(x)(x∈R)的图象与y=|log5x|的图象的交点个数为________.
三、解答题
17、已知全集集合,,,若,求实数的取值范围.
18、已知函数
f(x)
求函数f(x)的解析式;
(2) 设k>1,解关于x的不等式:
19、如图,四棱锥的底面为正方形,侧棱底面,且,分别是线段的中点.
(Ⅰ)求证://平面;(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
20、已知m∈R,设P:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立。
Q:函数f(x)=x3+(m+)x+6在(-∞,+ ∞)上有极值。
求使P正确且Q正确的m的取值范围。
21.已知二次函数f (x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c∈R,且满足a>b>c, f(1)=0.
(1)证明:函数f(x)与g(x)的图像交于不同的两点A、B;
(2)若函数F(x)=f(x)-g(x)在[2,3]上的最小值为9,最大值为21,试求a、b的值.
(3)求线段AB在x轴上的射影A1B1的长的取值范围.
22、已知函数(a为常数)是R上的奇函数,函数
是区间[-1,1]上的减函数.
(I)求a的值;
(II)若上恒成立,求t的取值范围;
(III)讨论关于x的方程的根的个数.
同课章节目录
