四川省攀枝花市米易中学2012届高三9月月考数学(文)试题
文档属性
| 名称 | 四川省攀枝花市米易中学2012届高三9月月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 218.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-08 00:00:00 | ||
图片预览


文档简介
第一卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,将正确答案写在答题卷上,否则视为零分)
1、已知集合A={x},B={x},则AB=( )
(A) {x} (B){x} (C){x} (D){x}
2、“x=3”是“x2=9”的( )
(A)充分而不必要的条件 (B)必要而不充分的条件
(C)充要条件 (D)既不充分也不必要的条件
3、若是真命题,是假命题,则( )
(A)是真命题 (B)是假命题 (C)是真命题 (D)是真命题
4、下列函数中,既是偶函数又在单调递增的函数是( )
(A) (B) (C) (D)
5、函数的y=(x≤-1)反函数是( )
A. y=-(x≥0) B. y=(x≥0)
C. y=-(x≥) D. y=(x≥)
6、方程在内( )
(A)没有根 (B)有且仅有一个根 (C) 有且仅有两个根 (D)有无穷多个根
7、如果,那么( )
(A) (B) (C) (D)
8、为了得到函数y=2x-3-1的图象,只需把函数y=2x的图象上所有的点( )
A. 向右平移3个单位长度,再向下平移1个单位长度
B. 向左平移3个单位长度,再向下平移1个单位长度
C. 向右平移3个单位长度,再向上平移1个单位长度
D. 向左平移3个单位长度,再向上平移1个单位长度
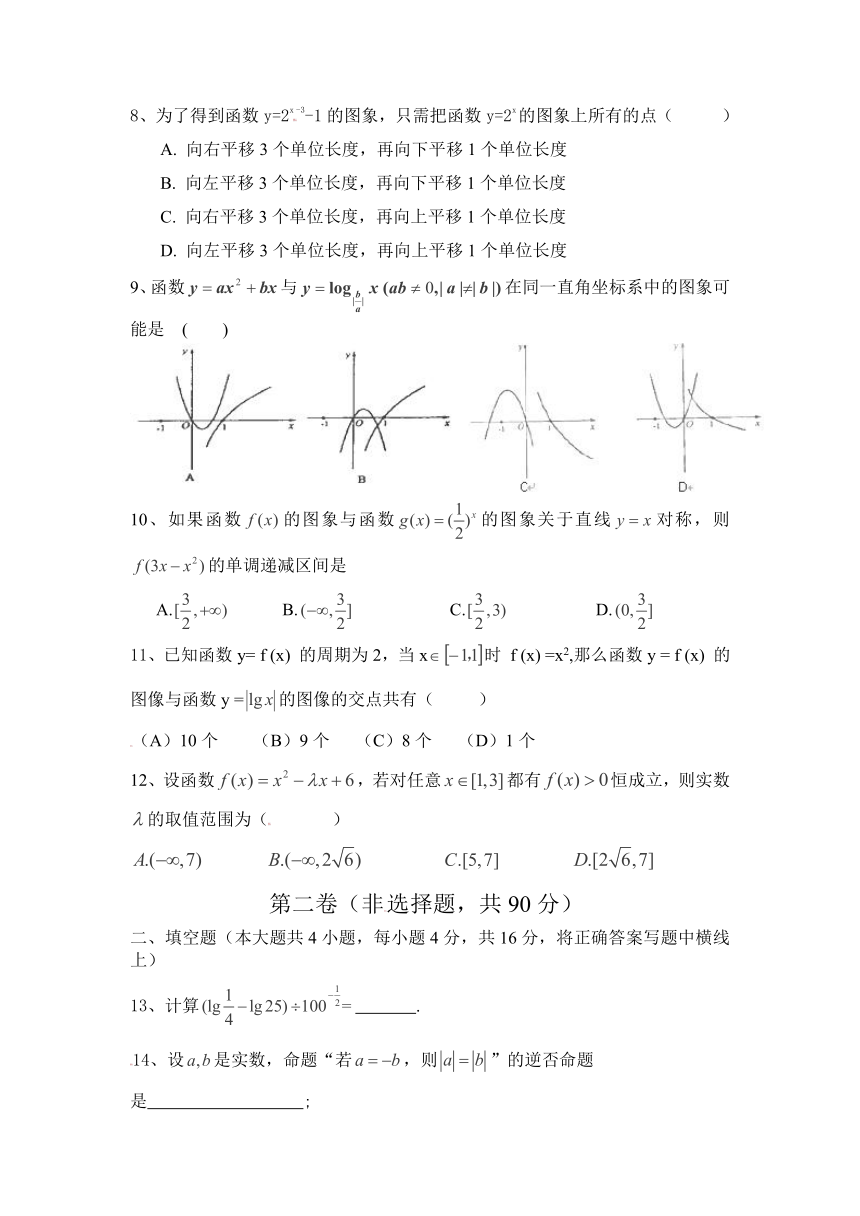
9、函数与在同一直角坐标系中的图象可能是 ( )
10、如果函数的图象与函数的图象关于直线对称,则的单调递减区间是
A. B. C. D.
11、已知函数y= f (x) 的周期为2,当x时 f (x) =x2,那么函数y = f (x) 的图像与函数y =的图像的交点共有( )
(A)10个 (B)9个 (C)8个 (D)1个
12、设函数,若对任意都有恒成立,则实数的取值范围为( )
第二卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案写题中横线上)
13、计算 .
14、设是实数,命题“若,则”的逆否命题是 ;
15、设是定义在R上的奇函数,当x≤0时,=,则 .
16、函数的定义域是 .
三、解答题:本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤.
17、已知函数
(1)若的解集为,求实数的取值范围;
(2)在(1)的条件下,求函数f(x)在区间[0,3]的值域.
18、已知函数是奇函数,并且函数的图像经过点(1,3),
求:(1)求实数的值;(2)求函数的值域(12分)
19、在2008年北京奥运会羽毛球女单决赛中,中国运动员张宁以2:1力克排名世界第一的队友谢杏芳,蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜,比赛结束),且各局之间互不影响.根据两人以往的交战成绩分析,谢杏芳在前两局的比赛中每局获胜的概率是0.6,但张宁在前二局战成1:1的情况下,在第三局中凭借过硬的心理素质,获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.
(1)求张宁以2:1获胜的概率;
(2)求张宁失利的概率. (12分)
20、已知集合,
(1)当时,求; (2)求使的实数的取值范围(12分)
21、直三棱柱ABC-A1B1C1中, AC=BC=AA1=2,∠ACB=90.E为BB1的中点,D点在AB上且DE=.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE的体积.
22、定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3)+f(3-9-2)<0对任意x∈R恒成立,求实数k的取值范围.(14分)
四川省米易中学校高2012级2011年九月月考数学试题(文科)
第一卷(选择题60分)
一、选择题(本大题共12小题,每小题5分,共60分)
二、填空题13、 -20 14、 若则 15、 -3 16、(-3,2)
三、解答题
17、解析 (1),;(2)
(2)由(1)知………(7分)
当时,当且仅当
即时取等号…(10分)
当时,
当且仅当即时取等号……………(13分)
综上可知函数的值域为…………(12分)
19、解:(1)张宁以2:1获胜即前两局战成1:1,第三局张宁胜.
. ………………………………6分
(2) 张宁失利包括0:2和1:2两种情况:
…………12分
20、
∴
=2×2-××2-××1-×2×1=
∴ VA1-CDE =VC-A1DE = ×SA1DE ×CD= ××=1
∴ 三棱锥A1-CDE的体积为1. -------------------------12分
22、解:(1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.
(2)解:f(3)=log3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k·3)<-f(3-9-2)=f(-3+9+2), k·3<-3+9+2,
3-(1+k)·3+2>0对任意x∈R成立.
令t=3>0,问题等价于t-(1+k)t+2>0对任意t>0恒成立.
一、选择题(本大题共12小题,每小题5分,共60分,将正确答案写在答题卷上,否则视为零分)
1、已知集合A={x},B={x},则AB=( )
(A) {x} (B){x} (C){x} (D){x}
2、“x=3”是“x2=9”的( )
(A)充分而不必要的条件 (B)必要而不充分的条件
(C)充要条件 (D)既不充分也不必要的条件
3、若是真命题,是假命题,则( )
(A)是真命题 (B)是假命题 (C)是真命题 (D)是真命题
4、下列函数中,既是偶函数又在单调递增的函数是( )
(A) (B) (C) (D)
5、函数的y=(x≤-1)反函数是( )
A. y=-(x≥0) B. y=(x≥0)
C. y=-(x≥) D. y=(x≥)
6、方程在内( )
(A)没有根 (B)有且仅有一个根 (C) 有且仅有两个根 (D)有无穷多个根
7、如果,那么( )
(A) (B) (C) (D)
8、为了得到函数y=2x-3-1的图象,只需把函数y=2x的图象上所有的点( )
A. 向右平移3个单位长度,再向下平移1个单位长度
B. 向左平移3个单位长度,再向下平移1个单位长度
C. 向右平移3个单位长度,再向上平移1个单位长度
D. 向左平移3个单位长度,再向上平移1个单位长度
9、函数与在同一直角坐标系中的图象可能是 ( )
10、如果函数的图象与函数的图象关于直线对称,则的单调递减区间是
A. B. C. D.
11、已知函数y= f (x) 的周期为2,当x时 f (x) =x2,那么函数y = f (x) 的图像与函数y =的图像的交点共有( )
(A)10个 (B)9个 (C)8个 (D)1个
12、设函数,若对任意都有恒成立,则实数的取值范围为( )
第二卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案写题中横线上)
13、计算 .
14、设是实数,命题“若,则”的逆否命题是 ;
15、设是定义在R上的奇函数,当x≤0时,=,则 .
16、函数的定义域是 .
三、解答题:本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤.
17、已知函数
(1)若的解集为,求实数的取值范围;
(2)在(1)的条件下,求函数f(x)在区间[0,3]的值域.
18、已知函数是奇函数,并且函数的图像经过点(1,3),
求:(1)求实数的值;(2)求函数的值域(12分)
19、在2008年北京奥运会羽毛球女单决赛中,中国运动员张宁以2:1力克排名世界第一的队友谢杏芳,蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜,比赛结束),且各局之间互不影响.根据两人以往的交战成绩分析,谢杏芳在前两局的比赛中每局获胜的概率是0.6,但张宁在前二局战成1:1的情况下,在第三局中凭借过硬的心理素质,获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.
(1)求张宁以2:1获胜的概率;
(2)求张宁失利的概率. (12分)
20、已知集合,
(1)当时,求; (2)求使的实数的取值范围(12分)
21、直三棱柱ABC-A1B1C1中, AC=BC=AA1=2,∠ACB=90.E为BB1的中点,D点在AB上且DE=.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE的体积.
22、定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3)+f(3-9-2)<0对任意x∈R恒成立,求实数k的取值范围.(14分)
四川省米易中学校高2012级2011年九月月考数学试题(文科)
第一卷(选择题60分)
一、选择题(本大题共12小题,每小题5分,共60分)
二、填空题13、 -20 14、 若则 15、 -3 16、(-3,2)
三、解答题
17、解析 (1),;(2)
(2)由(1)知………(7分)
当时,当且仅当
即时取等号…(10分)
当时,
当且仅当即时取等号……………(13分)
综上可知函数的值域为…………(12分)
19、解:(1)张宁以2:1获胜即前两局战成1:1,第三局张宁胜.
. ………………………………6分
(2) 张宁失利包括0:2和1:2两种情况:
…………12分
20、
∴
=2×2-××2-××1-×2×1=
∴ VA1-CDE =VC-A1DE = ×SA1DE ×CD= ××=1
∴ 三棱锥A1-CDE的体积为1. -------------------------12分
22、解:(1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.
(2)解:f(3)=log3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k·3)<-f(3-9-2)=f(-3+9+2), k·3<-3+9+2,
3-(1+k)·3+2>0对任意x∈R成立.
令t=3>0,问题等价于t-(1+k)t+2>0对任意t>0恒成立.
同课章节目录
