苏教版六年级数学下册《转化的策略解决问题》ppt课件
文档属性
| 名称 | 苏教版六年级数学下册《转化的策略解决问题》ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-08 17:54:19 | ||
图片预览


文档简介
(共23张PPT)
苏教版六年级数学下册
教学目标
1.在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3. 进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验。
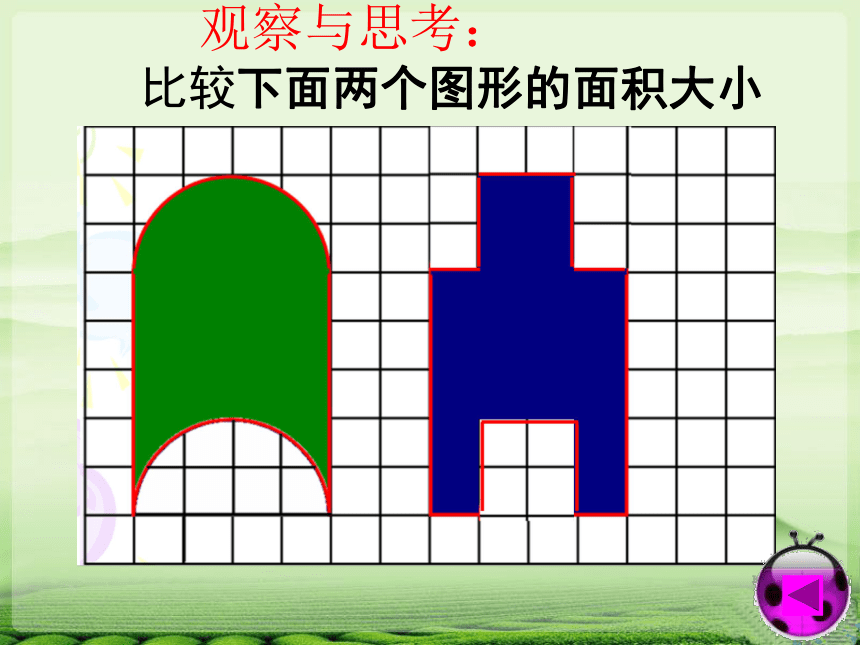
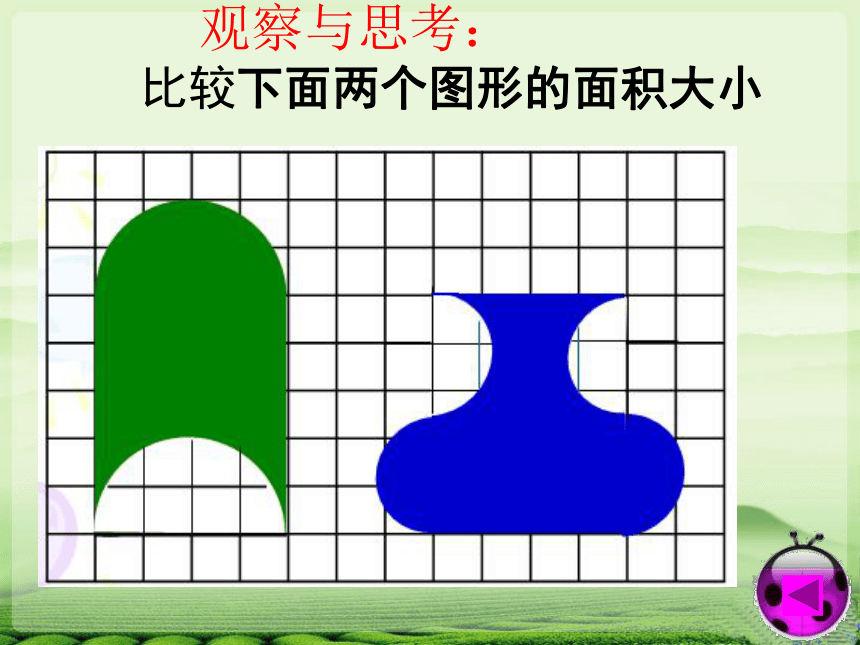
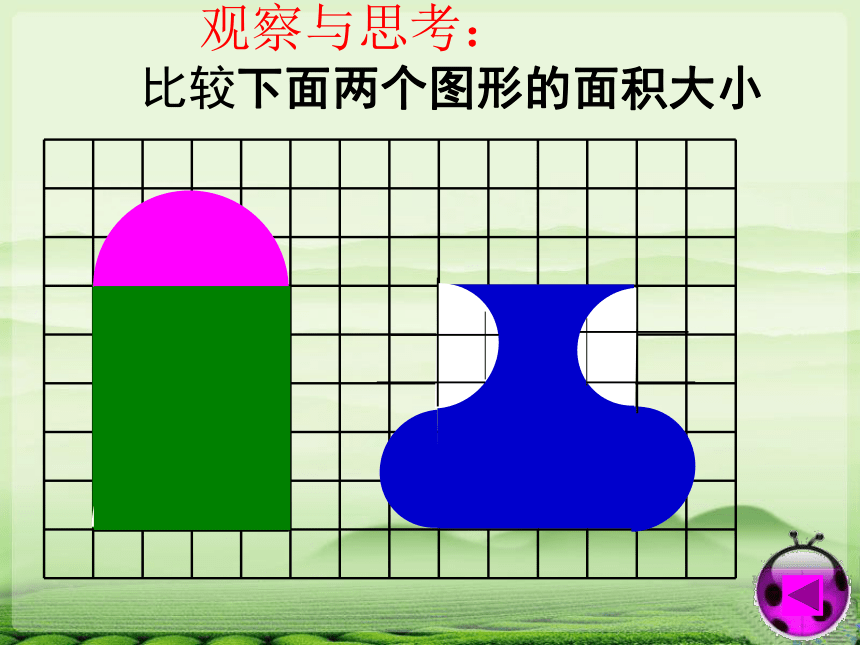
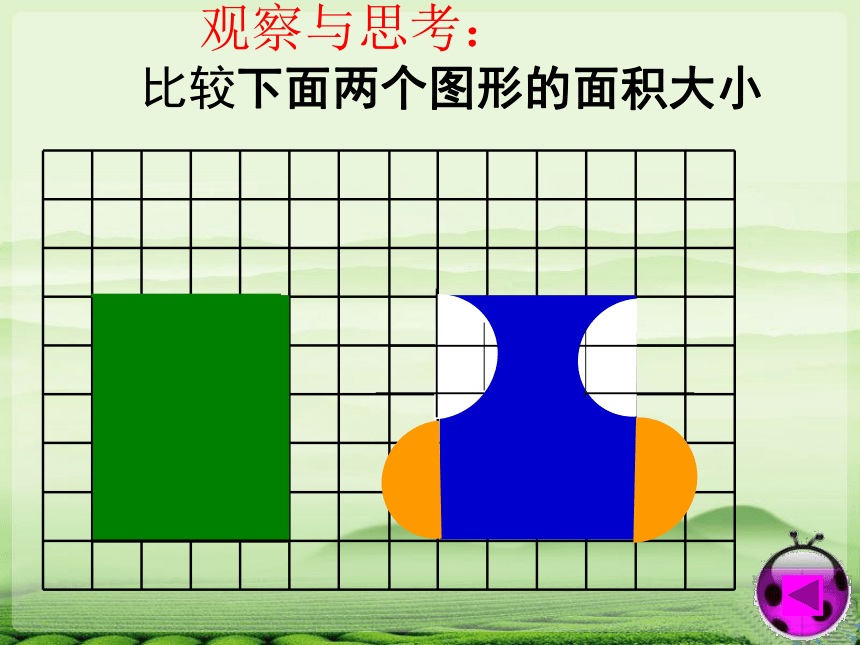
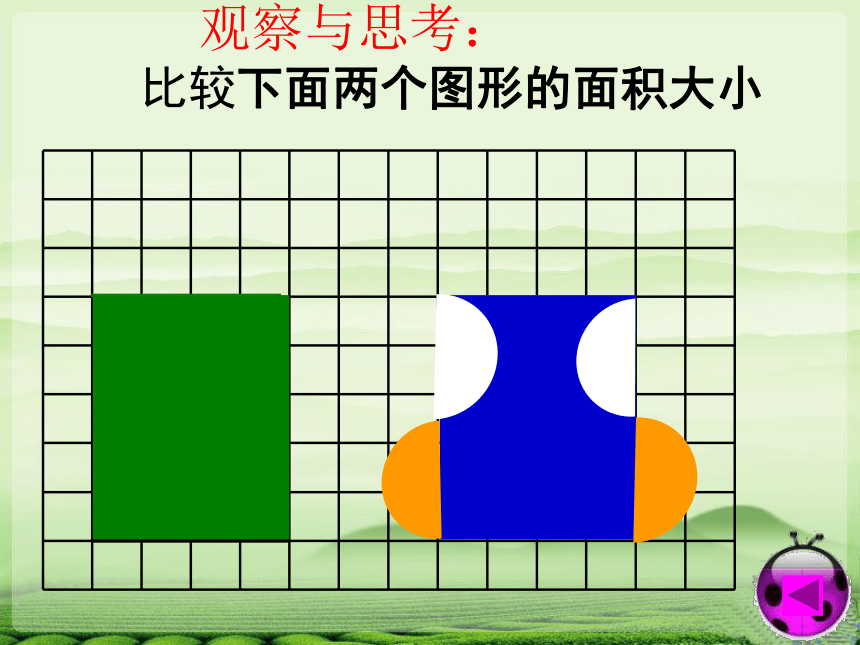
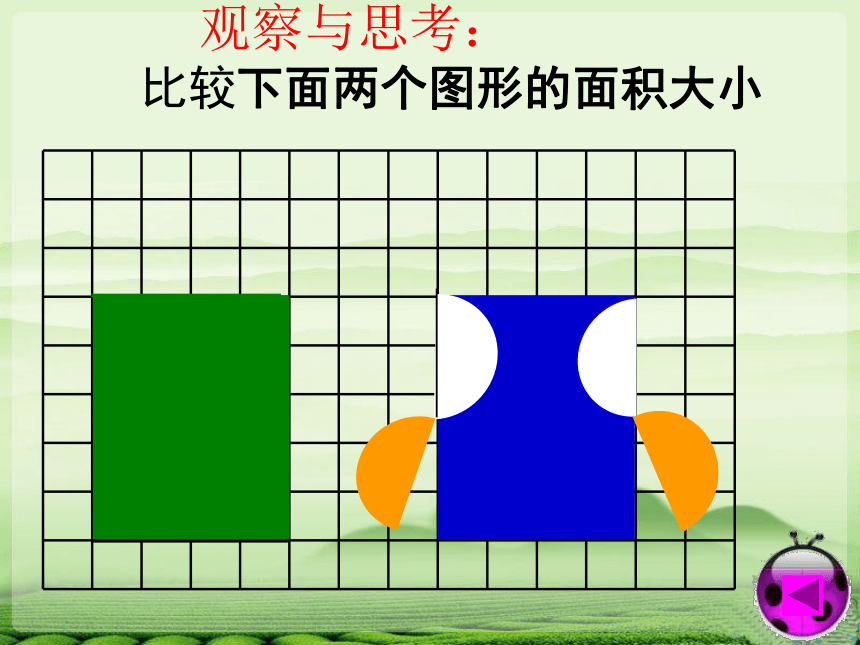
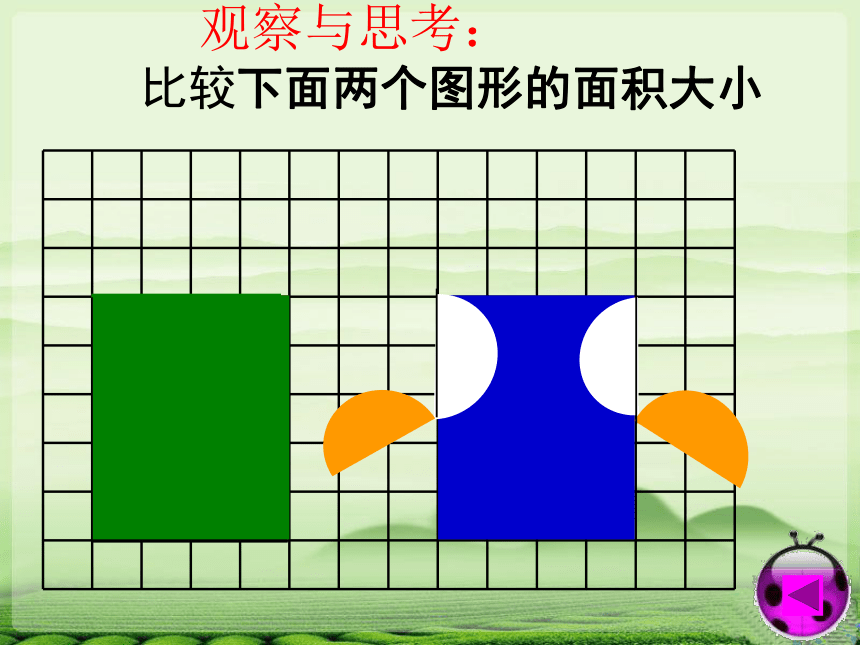
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
运用了什么策略?
回顾一下,我们曾经运用转化的策略解决过哪些图形问题?
推导平行四边形的面积公式时,把平行四边形转化成长方形。
计算圆柱的体积时,把圆柱转化成长方体。
例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm
例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm
练一练
用分数表示各图中的涂色部分
( )
( )
( )
( )
( )
( )
上页
试试
如图,正方形的边长是4厘米。E、F分别是BC和CD的中点,求阴影部分的面积。
A
B
C
D
E
F
用转化的策略解决问题
数学活动的实质就是思维的转化过程。
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
掌握转化的策略,对学好数学至关重要。
多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。
用转化的策略解决问题
苏教版六年级数学下册
教学目标
1.在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3. 进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验。
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
观察与思考: 比较下面两个图形的面积大小
运用了什么策略?
回顾一下,我们曾经运用转化的策略解决过哪些图形问题?
推导平行四边形的面积公式时,把平行四边形转化成长方形。
计算圆柱的体积时,把圆柱转化成长方体。
例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm
例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm
练一练
用分数表示各图中的涂色部分
( )
( )
( )
( )
( )
( )
上页
试试
如图,正方形的边长是4厘米。E、F分别是BC和CD的中点,求阴影部分的面积。
A
B
C
D
E
F
用转化的策略解决问题
数学活动的实质就是思维的转化过程。
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
掌握转化的策略,对学好数学至关重要。
多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。
用转化的策略解决问题
