广东省中山一中2011-2012学年高二下学期期中试题数学文
文档属性
| 名称 | 广东省中山一中2011-2012学年高二下学期期中试题数学文 |  | |
| 格式 | zip | ||
| 文件大小 | 224.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-08 20:48:14 | ||
图片预览


文档简介
中山一中高二下数学第一次段考试题(文科)
参考公式:,
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 点的直角坐标化成极坐标为( )
A B ( http: / / wxc. / ) C D ( http: / / wxc. / )
2.在同一坐标系中,将曲线变为曲线的伸缩变换是( )
A B ( http: / / wxc. / ) C D ( http: / / wxc. / )
3.已知是纯虚数,是实数,那么等于A B ( http: / / wxc. / ) C D ( http: / / wxc. / )
4. “是无限不循环小数,所以是无理数”,以上推理( )
A. 缺少小前提,小前提是无理数都是无限不循环小数
B. 缺少大前提,大前提是无理数都是无限不循环小数
C. 缺少小前提,小前提是无限不循环小数都是无理数
D. 缺少大前提,大前提是无限不循环小数都是无理数
5.条件有意义,条件,
则是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
图1-2
6.执行如图1-2所示的程序框图,若输入的值为,则输出的值为( )
A. B. C. D.
7.下列是全称命题且是真命题的是 ( )
A. B.
C. D.
8. 复数(其中为参数)在复平面内对应的点的轨迹方程是( )
A. B.
C. D.
9.是曲线上任意一点,点到直线距离的最大值为( )
A. B. C. D.
10.椭圆上的点到直线的最大距离为( )
A. B. C. D.
二、填空题:(本大题共4小题,每小题5分,共20分)
11. 命题“”的否定是_____________________________ .
12.把曲线的极坐标方程化为曲线的标准方程为 _________ .
13. 下列四个命题:①“等边三角形的三个内角都是”的逆命题;②“全等三角形的面积相等”的否命题;③“若,则方程有实根”的逆否命题;④参数方程表示的曲线是双曲线.其中真命题的是________________.
14. 已知的三边长为,内切圆半径为(用),则;类比这一结论有:若三棱锥的内切球半径为,则三棱锥体积 .
中山一中2011-2012学年度高二下数学
第一次段考试题(文科)答题卷
得分__________
一、选择题:(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:(每小题5分,共20分)
11._____________________________;12. _____________________________;
13._____________________________;14. _____________________________.
三.解答题:(共80分)
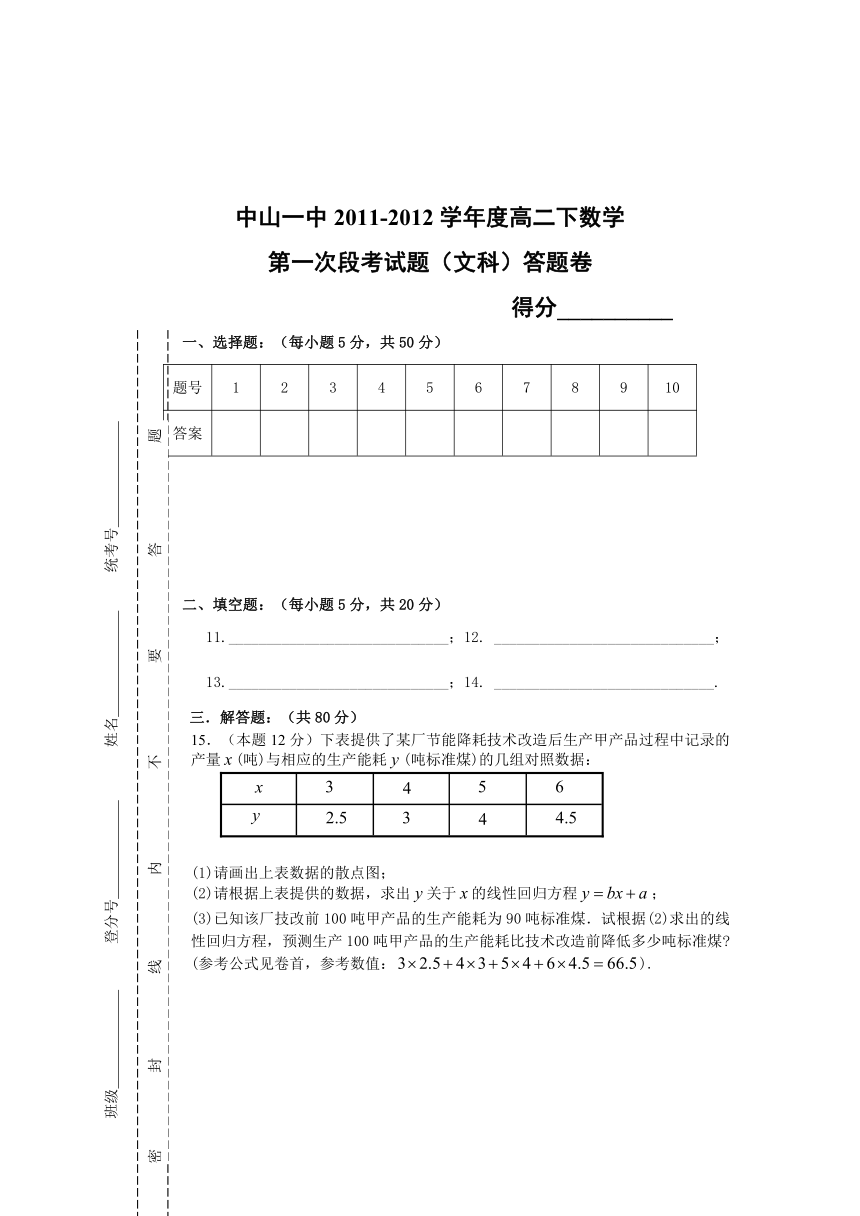
15.(本题12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出关于的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤 (参考公式见卷首,参考数值:).
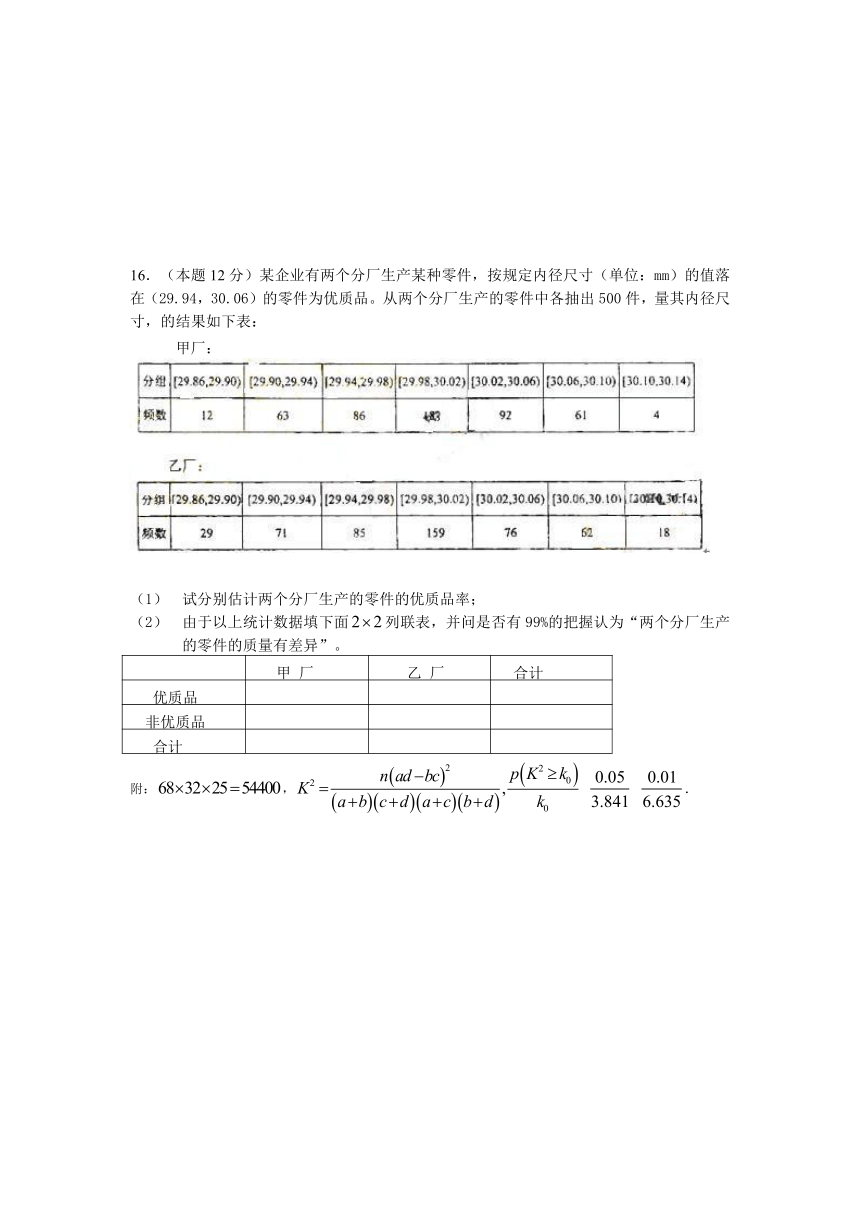
16.(本题12分)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
试分别估计两个分厂生产的零件的优质品率;
由于以上统计数据填下面列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
甲 厂 乙 厂 合计
优质品
非优质品
合计
附:, .
17.(本题14分)已知,求证:关于的三个方程,,中至少有一个方程有实数根.
18.(本题14分)设命题:,其中,命题:,
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
19.(本题14分)如图,在圆内画条线段,将圆分割成两部分;画条相交线段,彼此分割成条线段,将圆分割成部分;画条线段,彼此最多分割成条线段,将圆最多分割成部分;画条线段,彼此最多分割成条线段,将圆最多分割成部分.
(1)猜想:圆内两两相交的条线段,彼此最多分割成多少条线段?
(2)记在圆内画条线段,将圆最多分割成部分,归纳出与的关系.
(3)猜想数列的通项公式,根据与的关系及数列的知识,证明你的猜想是否成立.
20.(本题14分)在平面直角坐标系中,曲线C1的参数方程为,
(为参数),曲线C2的参数方程为(,为参数),在以O为极点,
轴的正半轴为极轴的极坐标系中,射线与C1,C2各有一个交点.当时,
这两个交点间的距离为,当时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当时,l与C1,C2的交点分别为A1,B1,当时,l与C1,C2的交点
分别为A2,B2,求四边形A1A2B2B1的面积.中山一中2011-2012学年度高二下数学
第一次段考试题(文科)答案卷
一、选择题 DBCDA CBCCB
二、填空题 11、 12、
13、①③④ 14、
15、解:(1)如图
……………………………………3分
(2)由对照数据,计算得: ; ……………………7分
所求的回归方程为 ………………………9分
(3)吨,
预测生产100吨甲产品的生产能耗比技改前降低(吨)……………………12分
16、解:(Ⅰ)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为 ………4分
(Ⅱ)
甲厂 乙厂 合计
优质品 360 320 680
非优质品 140 180 320
合计 500 500 1000
……8分
………………………………10分
所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 ……12分
17、解:假设三个方程都没有实根, ………………………………2分
则三个方程中:它们的判别式都小于,即
即 ………………………………8分
故, ………………………………10分
这与矛盾,所以假设不成立, …………………………12分
故三个方程中至少有一个方程有实数根. ………………………………14分
18、解:(1):,又,所以 ………………………………2分
: ………………………………4分
当时,:,若为真,则,所以
故实数的取值范围为. ………………………………8分
(2)是的充分不必要条件,即
故,.
所以的取值范围为. ………………………………14分
19、(1)彼此最多分割成条线段. ………………………………4分
(2)由已知得 ………………………………8分
(3)
………………………………14分
20、解:(1)C1是圆,C2是椭圆. ………………………………2分
因为α=0,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),
因为这两点间的距离为2,所以a=3. ………………………………4分
因为α=,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
………………………………6分
(2)C1,C2的普通方程分别为x2+y2=1和+y2=1. ………………………8分
因为α=,射线l与C1交点A1的横坐标为x=,与C2交点B1的横坐标为x′=.……10分
因为α=-,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,射线l与C1交点A1的横坐标为x=,与C2交点B1的横坐标为x′=因此四边形A1A2B2B1为梯形.…………12分
故四边形A1A2B2B1的面积为=. ………………………14分
.
班级 登分号 姓名 统考号
密 封 线 内 不 要 答 题
密 封 线 内 不 要 答 题
参考公式:,
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 点的直角坐标化成极坐标为( )
A B ( http: / / wxc. / ) C D ( http: / / wxc. / )
2.在同一坐标系中,将曲线变为曲线的伸缩变换是( )
A B ( http: / / wxc. / ) C D ( http: / / wxc. / )
3.已知是纯虚数,是实数,那么等于A B ( http: / / wxc. / ) C D ( http: / / wxc. / )
4. “是无限不循环小数,所以是无理数”,以上推理( )
A. 缺少小前提,小前提是无理数都是无限不循环小数
B. 缺少大前提,大前提是无理数都是无限不循环小数
C. 缺少小前提,小前提是无限不循环小数都是无理数
D. 缺少大前提,大前提是无限不循环小数都是无理数
5.条件有意义,条件,
则是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
图1-2
6.执行如图1-2所示的程序框图,若输入的值为,则输出的值为( )
A. B. C. D.
7.下列是全称命题且是真命题的是 ( )
A. B.
C. D.
8. 复数(其中为参数)在复平面内对应的点的轨迹方程是( )
A. B.
C. D.
9.是曲线上任意一点,点到直线距离的最大值为( )
A. B. C. D.
10.椭圆上的点到直线的最大距离为( )
A. B. C. D.
二、填空题:(本大题共4小题,每小题5分,共20分)
11. 命题“”的否定是_____________________________ .
12.把曲线的极坐标方程化为曲线的标准方程为 _________ .
13. 下列四个命题:①“等边三角形的三个内角都是”的逆命题;②“全等三角形的面积相等”的否命题;③“若,则方程有实根”的逆否命题;④参数方程表示的曲线是双曲线.其中真命题的是________________.
14. 已知的三边长为,内切圆半径为(用),则;类比这一结论有:若三棱锥的内切球半径为,则三棱锥体积 .
中山一中2011-2012学年度高二下数学
第一次段考试题(文科)答题卷
得分__________
一、选择题:(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:(每小题5分,共20分)
11._____________________________;12. _____________________________;
13._____________________________;14. _____________________________.
三.解答题:(共80分)
15.(本题12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出关于的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤 (参考公式见卷首,参考数值:).
16.(本题12分)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
试分别估计两个分厂生产的零件的优质品率;
由于以上统计数据填下面列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
甲 厂 乙 厂 合计
优质品
非优质品
合计
附:, .
17.(本题14分)已知,求证:关于的三个方程,,中至少有一个方程有实数根.
18.(本题14分)设命题:,其中,命题:,
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
19.(本题14分)如图,在圆内画条线段,将圆分割成两部分;画条相交线段,彼此分割成条线段,将圆分割成部分;画条线段,彼此最多分割成条线段,将圆最多分割成部分;画条线段,彼此最多分割成条线段,将圆最多分割成部分.
(1)猜想:圆内两两相交的条线段,彼此最多分割成多少条线段?
(2)记在圆内画条线段,将圆最多分割成部分,归纳出与的关系.
(3)猜想数列的通项公式,根据与的关系及数列的知识,证明你的猜想是否成立.
20.(本题14分)在平面直角坐标系中,曲线C1的参数方程为,
(为参数),曲线C2的参数方程为(,为参数),在以O为极点,
轴的正半轴为极轴的极坐标系中,射线与C1,C2各有一个交点.当时,
这两个交点间的距离为,当时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当时,l与C1,C2的交点分别为A1,B1,当时,l与C1,C2的交点
分别为A2,B2,求四边形A1A2B2B1的面积.中山一中2011-2012学年度高二下数学
第一次段考试题(文科)答案卷
一、选择题 DBCDA CBCCB
二、填空题 11、 12、
13、①③④ 14、
15、解:(1)如图
……………………………………3分
(2)由对照数据,计算得: ; ……………………7分
所求的回归方程为 ………………………9分
(3)吨,
预测生产100吨甲产品的生产能耗比技改前降低(吨)……………………12分
16、解:(Ⅰ)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为 ………4分
(Ⅱ)
甲厂 乙厂 合计
优质品 360 320 680
非优质品 140 180 320
合计 500 500 1000
……8分
………………………………10分
所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 ……12分
17、解:假设三个方程都没有实根, ………………………………2分
则三个方程中:它们的判别式都小于,即
即 ………………………………8分
故, ………………………………10分
这与矛盾,所以假设不成立, …………………………12分
故三个方程中至少有一个方程有实数根. ………………………………14分
18、解:(1):,又,所以 ………………………………2分
: ………………………………4分
当时,:,若为真,则,所以
故实数的取值范围为. ………………………………8分
(2)是的充分不必要条件,即
故,.
所以的取值范围为. ………………………………14分
19、(1)彼此最多分割成条线段. ………………………………4分
(2)由已知得 ………………………………8分
(3)
………………………………14分
20、解:(1)C1是圆,C2是椭圆. ………………………………2分
因为α=0,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),
因为这两点间的距离为2,所以a=3. ………………………………4分
因为α=,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
………………………………6分
(2)C1,C2的普通方程分别为x2+y2=1和+y2=1. ………………………8分
因为α=,射线l与C1交点A1的横坐标为x=,与C2交点B1的横坐标为x′=.……10分
因为α=-,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,射线l与C1交点A1的横坐标为x=,与C2交点B1的横坐标为x′=因此四边形A1A2B2B1为梯形.…………12分
故四边形A1A2B2B1的面积为=. ………………………14分
.
班级 登分号 姓名 统考号
密 封 线 内 不 要 答 题
密 封 线 内 不 要 答 题
同课章节目录
