鲁教版九年级上册数学习题课件 第3章 阶段核心归类 二次函数的图象和性质的九种常见类型(共44张ppt)
文档属性
| 名称 | 鲁教版九年级上册数学习题课件 第3章 阶段核心归类 二次函数的图象和性质的九种常见类型(共44张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 878.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览










文档简介
二次函数的图象和性质的九种常见类型
阶段核心归类
鲁教版 九年级上
第三章 二次函数
1
2
3
4
5
6
7
8
答 案 呈 现
温馨提示:点击 进入讲评
习题链接
9
【2020·达州】如图,直线y1=kx与抛物线y2=ax2+bx+c交于A,B两点,则y=ax2+(b-k)x+c的图象可能是( )
1
B
【点拨】设y=y2-y1,
∵y1=kx,y2=ax2+bx+c,
∴y=ax2+(b-k)x+c,
由图象可知,在点A和点B之间,y>0,在点A的左侧或点B的右侧,y<0,
故选项B符合题意,选项A,C,D不符合题意.故选B.
2
(2)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围;
【2020·安徽】在平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),直线y=x+m经过点A,抛物线y=ax2+bx+1恰好经过A,B,C三点中的两点.
(1)判断点B是否在直线y=x+m上,并说明理由;
3
解:点B在直线y=x+m上.
理由如下:
∵直线y=x+m经过点A(1,2),
∴2=1+m,解得m=1,
∴直线的表达式为y=x+1.
把x=2代入y=x+1得y=3,
∴点B(2,3)在直线y=x+m上.
(2)求a,b的值;
(3)平移抛物线y=ax2+bx+1,使其顶点仍在直线y=x+m上,求平移后所得抛物线与y轴交点纵坐标的最大值.
4
【中考·杭州】设二次函数y=ax2+bx-(a+b)(a,b是常数,a≠0).
(1)判断该二次函数图象与x轴的交点的个数,说明理由.
解:令y=0,
则0=ax2+bx-(a+b),
∵Δ=b2-4a[-(a+b)]=b2+4ab+4a2=(2a+b)2≥0,
∴方程有两个不相等的实数根或两个相等的实数根.
∴二次函数图象与x轴的交点的个数有两个或一个.
(2)若该二次函数图象经过A(-1,4),B(0,-1),C(1,1)三个点中的两个,求该二次函数的表达式.
(3)若a+b<0,点P(2,m)(m>0)在该二次函数图象上,求证:a>0.
证明:当x=2时,y=m,
∴m=4a+2b-(a+b)=3a+b>0①,
∵a+b<0.
∴-a-b>0②,
①+②得2a>0,∴a>0.
【中考·牡丹江】如图,抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
(1)求抛物线的表达式及顶点D的坐标;
5
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为________.
6
【中考·郴州】设a,b是任意两个实数,用max{a,b}表示a,b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4.参照上面的材料,解答下列问题:
(1)max{5,2}=________,max{0,3}=________.
5
3
(2)若max{3x+1,-x+1}=-x+1,求x的取值范围.
解:∵max{3x+1,-x+1}=-x+1,
∴3x+1≤-x+1,解得x≤0.
(3)求函数y=x2-2x-4与y=-x+2的图象的交点坐标.函数y=x2-2x-4的图象如图所示,请你在图中作出函数y=-x+2的图象,并根据图象直接写出max{-x+2,x2-2x-4}的最小值.
7
【2020·雅安】已知二次函数y=x2+bx+c(a≠0)的图象与x轴交于A,B(1,0)两点,与y轴交于点C(0,-3).
(1)求二次函数的表达式及A点坐标.
(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标.
解:如图,连接AD,CD.
则当点D到直线AC的距离取得最大值时,
△DAC的面积最大.
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N,使以M,N,B,O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
解:存在.点N的坐标为(-2,-3)或(0,-3)或(2,5).
8
【2020·娄底】如图,抛物线经过点A(-3,0),B(1,0),C(0,3).
(1)求抛物线的表达式.
解:由题意可设抛物线的表达式为
y=a(x+3)(x-1),把C(0,3)的坐标代入,
可得a=-1,∴y=-(x+3)(x-1)=-x2-2x+3.
∴抛物线的表达式为y=-x2-2x+3.
(2)点P(m,n)是抛物线上的动点,当-3<m<0时,试确定m的值,使得△PAC的面积最大.
(3)抛物线上是否存在不同于点B的点D,满足DA2-DC2=6,若存在,请求出点D的坐标;若不存在,请说明理由.
解:存在.由A(-3,0),B(1,0),C(0,3),可得OA=3,OB=1,OC=3,BA=4.
则易得∠CAO=45°.
如图②,连接BC,则BC2=OB2+OC2=10,
∴BA2-BC2=6.
过点B作AC的垂线交抛物线于点D,交AC于点H,连接DC.
则∠DBA=∠CAO=45°,易得
DA2-DC2=HA2-HC2=BA2-BC2=6,
∵∠CAO=∠DBA,
∴点H在AB的垂直平分线上,即点H在抛物线的对称轴直线x=-1上,
∴点D与点C关于抛物线的对称轴直线x=-1对称.
∵C(0,3),∴点D的坐标为(-2,3).
9
②求此函数的最大值.
(2)已知线段AB的两个端点坐标分别为A(2,2),B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.
(3)当此函数图象上有4个点到x轴的距离等于4时,求n的取值范围.
阶段核心归类
鲁教版 九年级上
第三章 二次函数
1
2
3
4
5
6
7
8
答 案 呈 现
温馨提示:点击 进入讲评
习题链接
9
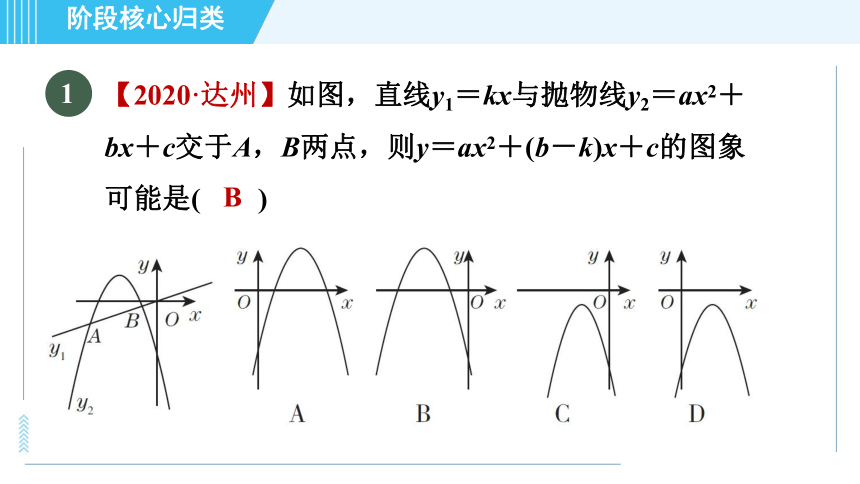
【2020·达州】如图,直线y1=kx与抛物线y2=ax2+bx+c交于A,B两点,则y=ax2+(b-k)x+c的图象可能是( )
1
B
【点拨】设y=y2-y1,
∵y1=kx,y2=ax2+bx+c,
∴y=ax2+(b-k)x+c,
由图象可知,在点A和点B之间,y>0,在点A的左侧或点B的右侧,y<0,
故选项B符合题意,选项A,C,D不符合题意.故选B.
2
(2)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围;
【2020·安徽】在平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),直线y=x+m经过点A,抛物线y=ax2+bx+1恰好经过A,B,C三点中的两点.
(1)判断点B是否在直线y=x+m上,并说明理由;
3
解:点B在直线y=x+m上.
理由如下:
∵直线y=x+m经过点A(1,2),
∴2=1+m,解得m=1,
∴直线的表达式为y=x+1.
把x=2代入y=x+1得y=3,
∴点B(2,3)在直线y=x+m上.
(2)求a,b的值;
(3)平移抛物线y=ax2+bx+1,使其顶点仍在直线y=x+m上,求平移后所得抛物线与y轴交点纵坐标的最大值.
4
【中考·杭州】设二次函数y=ax2+bx-(a+b)(a,b是常数,a≠0).
(1)判断该二次函数图象与x轴的交点的个数,说明理由.
解:令y=0,
则0=ax2+bx-(a+b),
∵Δ=b2-4a[-(a+b)]=b2+4ab+4a2=(2a+b)2≥0,
∴方程有两个不相等的实数根或两个相等的实数根.
∴二次函数图象与x轴的交点的个数有两个或一个.
(2)若该二次函数图象经过A(-1,4),B(0,-1),C(1,1)三个点中的两个,求该二次函数的表达式.
(3)若a+b<0,点P(2,m)(m>0)在该二次函数图象上,求证:a>0.
证明:当x=2时,y=m,
∴m=4a+2b-(a+b)=3a+b>0①,
∵a+b<0.
∴-a-b>0②,
①+②得2a>0,∴a>0.
【中考·牡丹江】如图,抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
(1)求抛物线的表达式及顶点D的坐标;
5
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为________.
6
【中考·郴州】设a,b是任意两个实数,用max{a,b}表示a,b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4.参照上面的材料,解答下列问题:
(1)max{5,2}=________,max{0,3}=________.
5
3
(2)若max{3x+1,-x+1}=-x+1,求x的取值范围.
解:∵max{3x+1,-x+1}=-x+1,
∴3x+1≤-x+1,解得x≤0.
(3)求函数y=x2-2x-4与y=-x+2的图象的交点坐标.函数y=x2-2x-4的图象如图所示,请你在图中作出函数y=-x+2的图象,并根据图象直接写出max{-x+2,x2-2x-4}的最小值.
7
【2020·雅安】已知二次函数y=x2+bx+c(a≠0)的图象与x轴交于A,B(1,0)两点,与y轴交于点C(0,-3).
(1)求二次函数的表达式及A点坐标.
(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标.
解:如图,连接AD,CD.
则当点D到直线AC的距离取得最大值时,
△DAC的面积最大.
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N,使以M,N,B,O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
解:存在.点N的坐标为(-2,-3)或(0,-3)或(2,5).
8
【2020·娄底】如图,抛物线经过点A(-3,0),B(1,0),C(0,3).
(1)求抛物线的表达式.
解:由题意可设抛物线的表达式为
y=a(x+3)(x-1),把C(0,3)的坐标代入,
可得a=-1,∴y=-(x+3)(x-1)=-x2-2x+3.
∴抛物线的表达式为y=-x2-2x+3.
(2)点P(m,n)是抛物线上的动点,当-3<m<0时,试确定m的值,使得△PAC的面积最大.
(3)抛物线上是否存在不同于点B的点D,满足DA2-DC2=6,若存在,请求出点D的坐标;若不存在,请说明理由.
解:存在.由A(-3,0),B(1,0),C(0,3),可得OA=3,OB=1,OC=3,BA=4.
则易得∠CAO=45°.
如图②,连接BC,则BC2=OB2+OC2=10,
∴BA2-BC2=6.
过点B作AC的垂线交抛物线于点D,交AC于点H,连接DC.
则∠DBA=∠CAO=45°,易得
DA2-DC2=HA2-HC2=BA2-BC2=6,
∵∠CAO=∠DBA,
∴点H在AB的垂直平分线上,即点H在抛物线的对称轴直线x=-1上,
∴点D与点C关于抛物线的对称轴直线x=-1对称.
∵C(0,3),∴点D的坐标为(-2,3).
9
②求此函数的最大值.
(2)已知线段AB的两个端点坐标分别为A(2,2),B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.
(3)当此函数图象上有4个点到x轴的距离等于4时,求n的取值范围.
