鲁教版九年级上册数学习题课件 第4章 全章热门考点整合应用(共28张ppt)
文档属性
| 名称 | 鲁教版九年级上册数学习题课件 第4章 全章热门考点整合应用(共28张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览







文档简介
全章热门考点整合应用
鲁教版 九年级上
第四章 投影与视图
1
2
3
4
5
6
7
8
答 案 呈 现
温馨提示:点击 进入讲评
习题链接
9
B
10
11
A
12
B
B
1
下列光线所形成是平行投影的是( )
A.太阳光线 B.台灯的光线
C.手电筒的光线 D.路灯的光线
A
2
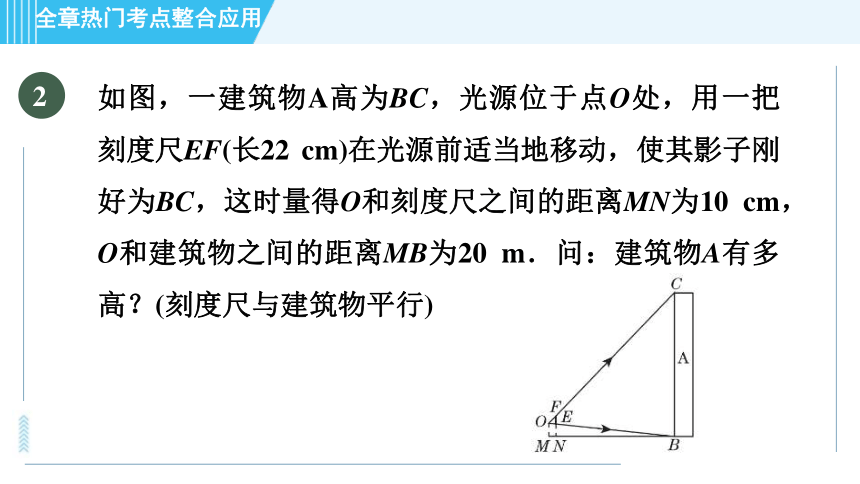
如图,一建筑物A高为BC,光源位于点O处,用一把刻度尺EF(长22 cm)在光源前适当地移动,使其影子刚好为BC,这时量得O和刻度尺之间的距离MN为10 cm,O和建筑物之间的距离MB为20 m.问:建筑物A有多高?(刻度尺与建筑物平行)
3
【2020·黄石】如图所示,该几何体的俯视图是( )
B
4
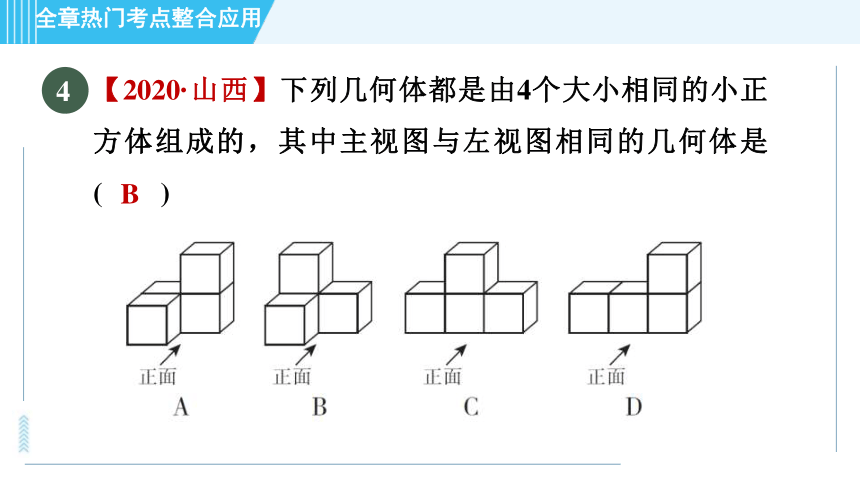
【2020·山西】下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )
B
【点拨】A.主视图底层是两个小正方形,上层右边是一个小正方形;左视图底层是两个小正方形,上层左边是一个小正方形,故本选项不合题意;B.主视图和左视图均为底层是两个小正方形,上层左边是一个小正方形,故本选项符合题意;C.主视图底层是三个小正方形,上层中间是一个小正方形;左视图是一列两个小正方形,故本选项不合题意;D.主视图底层是三个小正方形,上层最右边是一个小正方形;左视图是一列两个小正方形,故本选项不合题意.故选B.
5
如图①是由一些棱长都为1 cm的小正方体组成的简单几何体.
(1)该几何体的表面积为________;
26 cm2
(2)该几何体的主视图如图②中阴影部分所示,请在图②的方格纸中分别画出它的左视图和俯视图.
解:如图.
6
【2020·黑龙江】如图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则所需的小正方体的个数最多是( )
A.6 B.7
C.8 D.9
B
7
解:这种容器的三视图如图所示.
某种含盖的玻璃容器(透明)的外形如图所示,请你画出它的三视图.
8
小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图为小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
解:如图,AB即为所求.
(2)若已知小明身高是1.60 m,小明与小丽间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
9
学习投影后,小明和小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
解:如图.
(2)求路灯灯泡的垂直高度GH.
10
一种机器上有一个零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图.
解:如图.
11
如图,晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯(AB和CD)之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子(HE)长为3 m,左边的影子(HF)长为1.5 m,又知自己身高(GH)为1.80 m,两盏路灯的高相同,两盏路灯之间的距离(BD)为12 m,
求路灯的高.
12
某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B.(点B与河对岸岸边的一棵树的底部点D所确定的直线垂直于河岸)
(1)小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7 m.
(2)小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6 m,小明的眼睛距地面的距离CB=1.2 m.根据以上测量过程及测量数据,请你求出河宽BD.
鲁教版 九年级上
第四章 投影与视图
1
2
3
4
5
6
7
8
答 案 呈 现
温馨提示:点击 进入讲评
习题链接
9
B
10
11
A
12
B
B
1
下列光线所形成是平行投影的是( )
A.太阳光线 B.台灯的光线
C.手电筒的光线 D.路灯的光线
A
2
如图,一建筑物A高为BC,光源位于点O处,用一把刻度尺EF(长22 cm)在光源前适当地移动,使其影子刚好为BC,这时量得O和刻度尺之间的距离MN为10 cm,O和建筑物之间的距离MB为20 m.问:建筑物A有多高?(刻度尺与建筑物平行)
3
【2020·黄石】如图所示,该几何体的俯视图是( )
B
4
【2020·山西】下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )
B
【点拨】A.主视图底层是两个小正方形,上层右边是一个小正方形;左视图底层是两个小正方形,上层左边是一个小正方形,故本选项不合题意;B.主视图和左视图均为底层是两个小正方形,上层左边是一个小正方形,故本选项符合题意;C.主视图底层是三个小正方形,上层中间是一个小正方形;左视图是一列两个小正方形,故本选项不合题意;D.主视图底层是三个小正方形,上层最右边是一个小正方形;左视图是一列两个小正方形,故本选项不合题意.故选B.
5
如图①是由一些棱长都为1 cm的小正方体组成的简单几何体.
(1)该几何体的表面积为________;
26 cm2
(2)该几何体的主视图如图②中阴影部分所示,请在图②的方格纸中分别画出它的左视图和俯视图.
解:如图.
6
【2020·黑龙江】如图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则所需的小正方体的个数最多是( )
A.6 B.7
C.8 D.9
B
7
解:这种容器的三视图如图所示.
某种含盖的玻璃容器(透明)的外形如图所示,请你画出它的三视图.
8
小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图为小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
解:如图,AB即为所求.
(2)若已知小明身高是1.60 m,小明与小丽间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
9
学习投影后,小明和小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
解:如图.
(2)求路灯灯泡的垂直高度GH.
10
一种机器上有一个零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图.
解:如图.
11
如图,晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯(AB和CD)之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子(HE)长为3 m,左边的影子(HF)长为1.5 m,又知自己身高(GH)为1.80 m,两盏路灯的高相同,两盏路灯之间的距离(BD)为12 m,
求路灯的高.
12
某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B.(点B与河对岸岸边的一棵树的底部点D所确定的直线垂直于河岸)
(1)小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7 m.
(2)小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6 m,小明的眼睛距地面的距离CB=1.2 m.根据以上测量过程及测量数据,请你求出河宽BD.
