19.2.1矩形
图片预览


文档简介
(共27张PPT)
19.2.1矩形
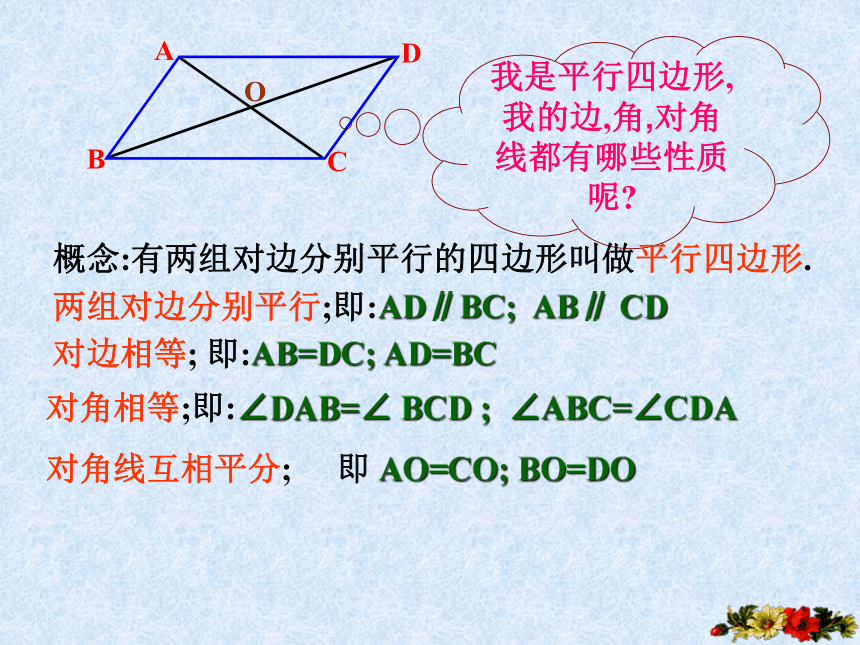
我是平行四边形,我的边,角,对角线都有哪些性质呢
概念:有两组对边分别平行的四边形叫做平行四边形.
O
A
B
D
C
两组对边分别平行;即:AD∥BC; AB∥ CD
对边相等; 即:AB=DC; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
对角线互相平分;
即 AO=CO; BO=DO
A
B
O
C
D
B
A
O
C
D
B
D
A
C
O
B
A
O
D
C
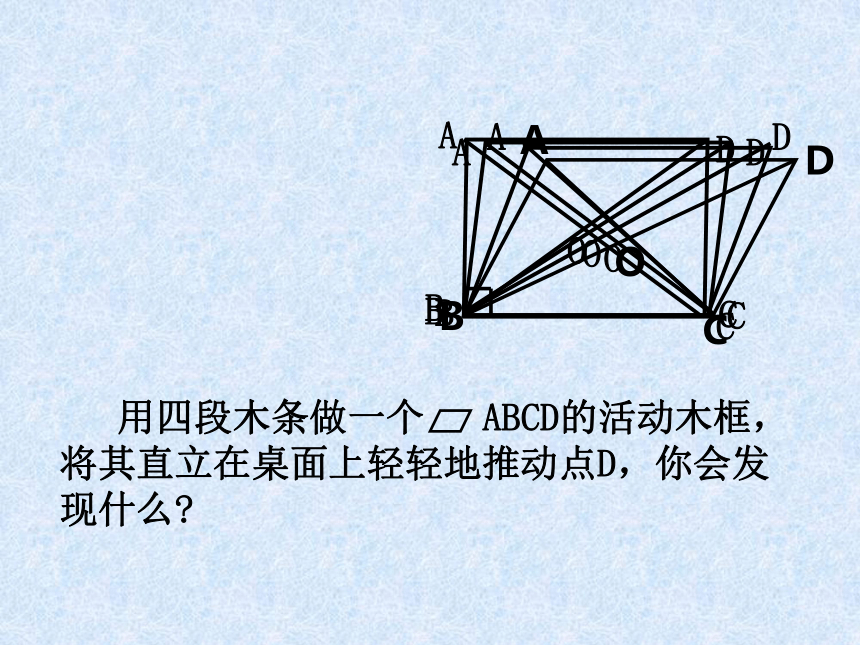
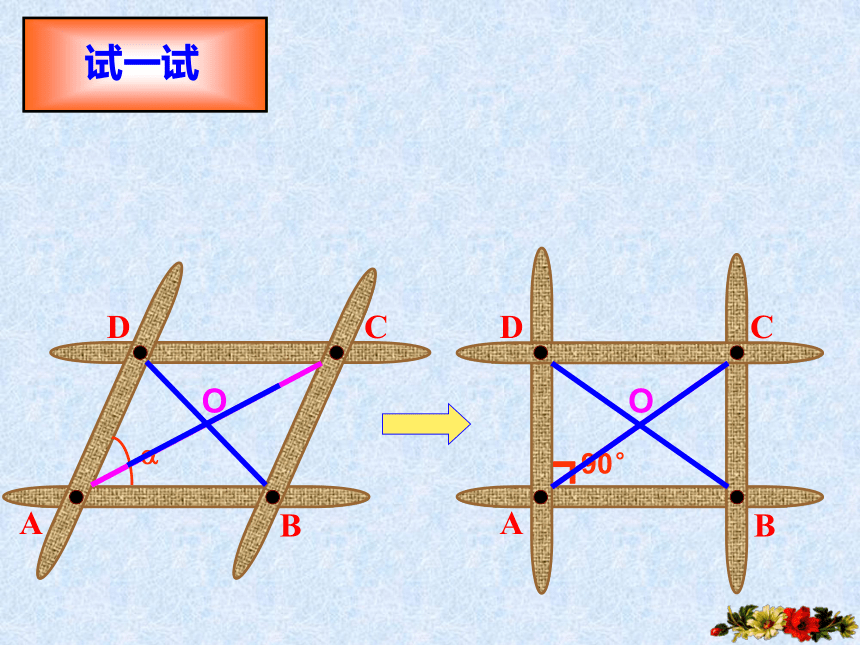
用四段木条做一个 ABCD的活动木框,将其直立在桌面上轻轻地推动点D,你会发现什么
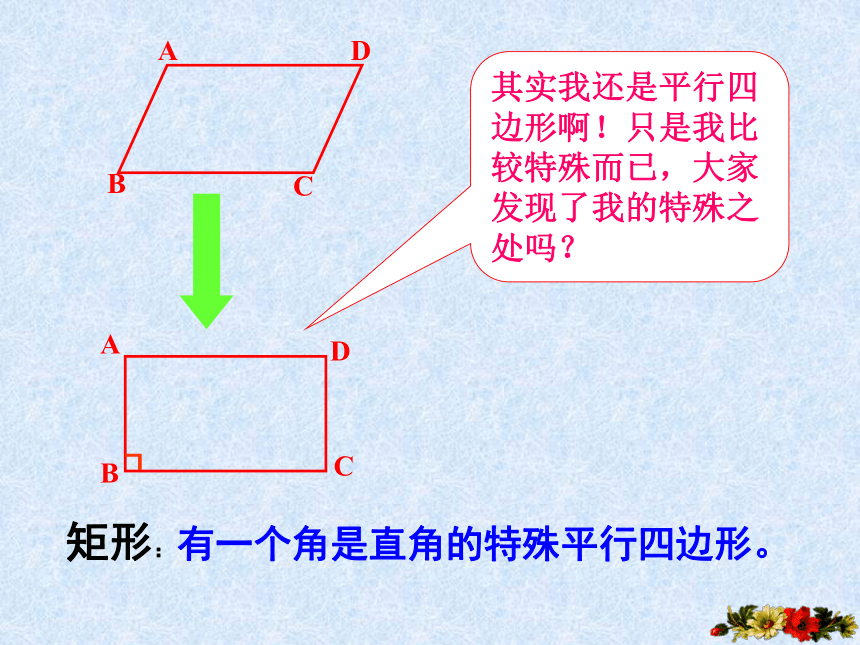
其实我还是平行四边形啊!只是我比较特殊而已,大家发现了我的特殊之处吗?
矩形:有一个角是直角的特殊平行四边形。
A
B
D
C
A
B
D
C
┒
矩形:
木门
纸张
电脑显示屏
有一个角是直角的平行四边形。
生活中的矩形图
怎样的平行四边形是矩形呢
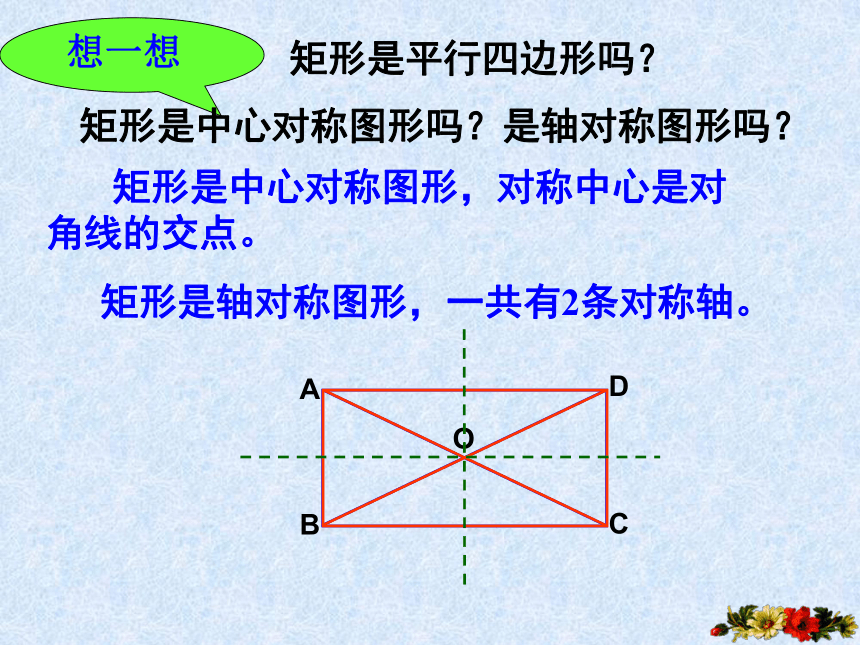
矩形是平行四边形吗?
想一想
矩形是中心对称图形,对称中心是对角线的交点。
矩形是轴对称图形,一共有2条对称轴。
矩形是中心对称图形吗?是轴对称图形吗?
A
B
C
D
O
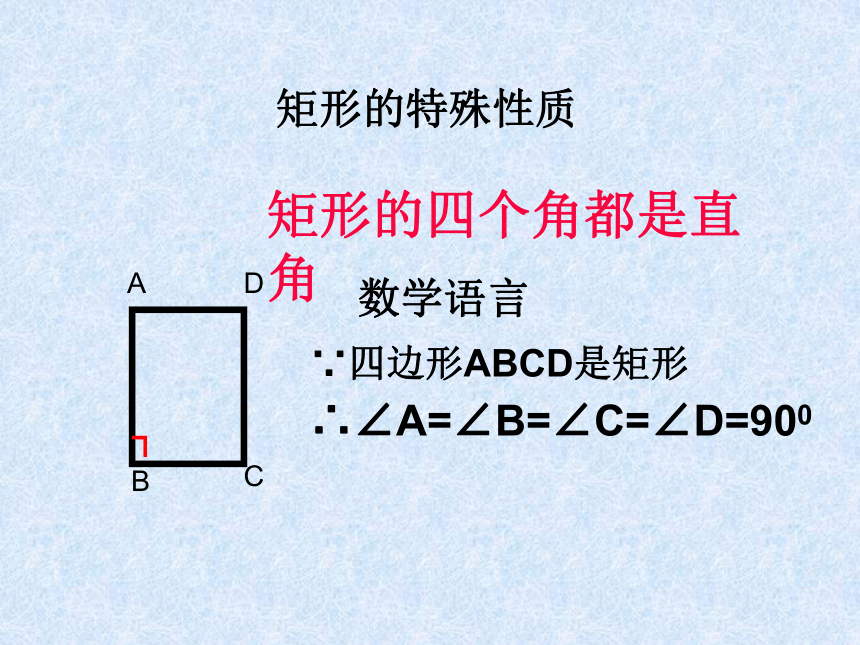
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
试一试
D
A
C
B
D
A
C
B
O
O
┓
90°
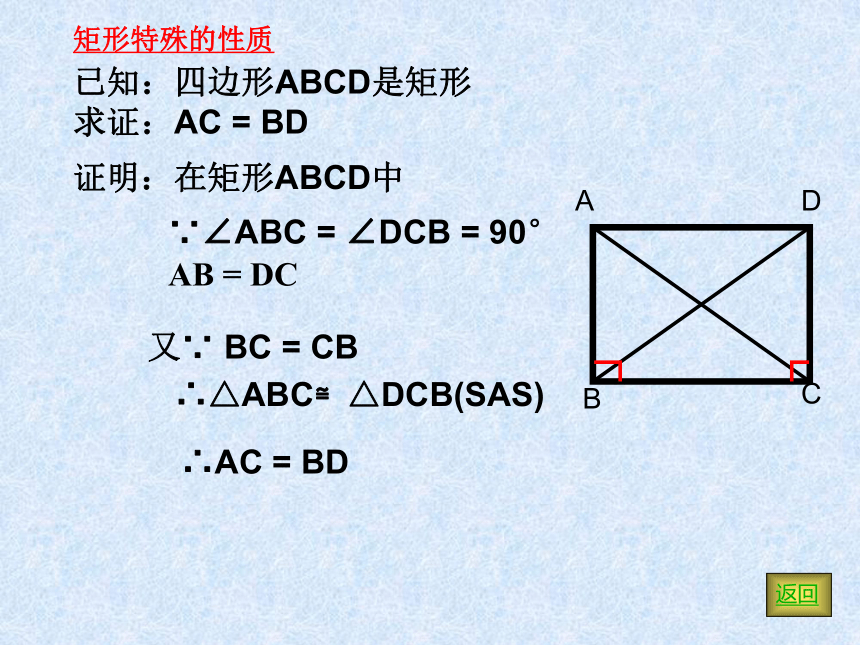
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
返回
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90° AB = DC
又∵ BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形特殊的性质
矩形的特殊性质
矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
这是矩形所特有的性质
O
直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半.
如图,矩形ABCD中,对角线AC、BD相
交于点O,请探讨OC与BD的关系
推论:直角三角形斜边上的中线等于斜边的一半.
已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
A
B
C
D
∵AD = BD , DE =CD
∴四边形ACBE是平行四边形
E
又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( )
由于CD= CE 所以CD = AB
返回
例1 已知:矩形ABCD的两条对角线相交于O,∠AOB=60°,AB = 4cm.
求矩形对角线的长
A
B
C
D
O
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分
∴ OA=OB.
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长
AC=BD = 2OA=2×4=8(cm).
练习:教材95页练习1
如图,在矩形ABCD中,找出相等的线段与相等的角。
A
D
C
B
O
想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三解形,有几对全等的等腰三角形?
小试牛刀
矩形具有而一般平行四边形不
具有的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
O
D
C
B
A
10
5
O
D
C
B
A
四边形ABCD是矩形
若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm,AB= _____cm
4
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线
若∠C=30°,AB=5㎝,则AC= ㎝, BD= ㎝.
10
5
已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。
例2 如图,在矩形ABCD中,AB=3, BC = 4, BE⊥AC于E.试求出AC、BE的长.
解:在矩形ABCD中,∠ABC = 90°,
AC =
=
=
又∵ S△ABC = AB·BC
∴ BE =
1
2
= 2.4
= AC·BE,
AB·BC
AC
=
3×4
5
A
B
D
C
E
┒
1
2
∵ AC>0∴AC=5
小结:
矩形:有一个角是直角的特殊平行四边形。
矩形的性质:
矩形的对角线相等且互相平分。
矩形具有平行四边形的所有性质;
另外:
矩形既是轴对称图形又是中心对称图形;
矩形的四个内角都是直角。
推论:直角三角形斜边上的中线等于斜边的一半.
作业: 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
A
B
C
D
O
A
D
C
B
E
1、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。
解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC
注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.
∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4
∵AE平分∠BAD
∴∠BAE=45°
∴AB=BE=4
∴BC=7
∴矩形ABCD的周长为22cm
1. 如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
E
A
B
D
C
练习
19.2.1矩形
我是平行四边形,我的边,角,对角线都有哪些性质呢
概念:有两组对边分别平行的四边形叫做平行四边形.
O
A
B
D
C
两组对边分别平行;即:AD∥BC; AB∥ CD
对边相等; 即:AB=DC; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
对角线互相平分;
即 AO=CO; BO=DO
A
B
O
C
D
B
A
O
C
D
B
D
A
C
O
B
A
O
D
C
用四段木条做一个 ABCD的活动木框,将其直立在桌面上轻轻地推动点D,你会发现什么
其实我还是平行四边形啊!只是我比较特殊而已,大家发现了我的特殊之处吗?
矩形:有一个角是直角的特殊平行四边形。
A
B
D
C
A
B
D
C
┒
矩形:
木门
纸张
电脑显示屏
有一个角是直角的平行四边形。
生活中的矩形图
怎样的平行四边形是矩形呢
矩形是平行四边形吗?
想一想
矩形是中心对称图形,对称中心是对角线的交点。
矩形是轴对称图形,一共有2条对称轴。
矩形是中心对称图形吗?是轴对称图形吗?
A
B
C
D
O
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
试一试
D
A
C
B
D
A
C
B
O
O
┓
90°
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
返回
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90° AB = DC
又∵ BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形特殊的性质
矩形的特殊性质
矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
这是矩形所特有的性质
O
直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半.
如图,矩形ABCD中,对角线AC、BD相
交于点O,请探讨OC与BD的关系
推论:直角三角形斜边上的中线等于斜边的一半.
已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
A
B
C
D
∵AD = BD , DE =CD
∴四边形ACBE是平行四边形
E
又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( )
由于CD= CE 所以CD = AB
返回
例1 已知:矩形ABCD的两条对角线相交于O,∠AOB=60°,AB = 4cm.
求矩形对角线的长
A
B
C
D
O
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分
∴ OA=OB.
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长
AC=BD = 2OA=2×4=8(cm).
练习:教材95页练习1
如图,在矩形ABCD中,找出相等的线段与相等的角。
A
D
C
B
O
想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三解形,有几对全等的等腰三角形?
小试牛刀
矩形具有而一般平行四边形不
具有的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
O
D
C
B
A
10
5
O
D
C
B
A
四边形ABCD是矩形
若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm,AB= _____cm
4
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线
若∠C=30°,AB=5㎝,则AC= ㎝, BD= ㎝.
10
5
已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。
例2 如图,在矩形ABCD中,AB=3, BC = 4, BE⊥AC于E.试求出AC、BE的长.
解:在矩形ABCD中,∠ABC = 90°,
AC =
=
=
又∵ S△ABC = AB·BC
∴ BE =
1
2
= 2.4
= AC·BE,
AB·BC
AC
=
3×4
5
A
B
D
C
E
┒
1
2
∵ AC>0∴AC=5
小结:
矩形:有一个角是直角的特殊平行四边形。
矩形的性质:
矩形的对角线相等且互相平分。
矩形具有平行四边形的所有性质;
另外:
矩形既是轴对称图形又是中心对称图形;
矩形的四个内角都是直角。
推论:直角三角形斜边上的中线等于斜边的一半.
作业: 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
A
B
C
D
O
A
D
C
B
E
1、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。
解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC
注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.
∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4
∵AE平分∠BAD
∴∠BAE=45°
∴AB=BE=4
∴BC=7
∴矩形ABCD的周长为22cm
1. 如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
E
A
B
D
C
练习
