2021-2022学年北师大版数学八上同步检测1.3勾股定理的应用(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版数学八上同步检测1.3勾股定理的应用(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 494.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 17:41:14 | ||
图片预览


文档简介
1.3
勾股定理的应用
一、选择题(共6小题;共30分)
1.
如图所示,在一段高为
,长为
的楼梯表面铺地毯,则地毯的长度至少是
A.
B.
C.
D.
2.
如图所示,一架梯子长
,斜靠在—面墙上,梯子顶端离地面
.现要使梯子顶端离地面
,则梯子的底部在水平面方向上要向左滑动
A.
B.
C.
D.
3.
某住宅小区有一块草坪,如图所示,已知
,,,
,且
,则这块草坪的面积是
A.
B.
C.
D.
4.
如图所示,圆柱形玻璃杯的高为
,底面周长为
,在杯内离杯底
的点
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁离杯上沿
与蜂蜜相对的点
处,则蚂蚁到达蜂蜜的最短距离为
A.
B.
C.
D.
5.
一架
长的梯子斜立在一堵竖直的墙上,这时梯足距离墙底
.如果梯子的顶端沿墙下滑
,那么梯足将滑动
A.
B.
C.
D.
6.
如图所示是一棱长为
的正方体,把它分成
个小正方体,每个小正方体的边长都是
.如果一只蚂蚁从点
爬到点
,那么
,
间的最短距离
满足
A.
B.
C.
D.
或
二、填空题(共6小题;共30分)
7.
城墙高
,城墙外有—条宽为
的护城河,那么一架长为
的梯子能否跨过护城河到达城墙的顶端?答:
?(选填“能”或“不能”).
8.
如图所示,—根木杆在离地面
处断裂,木杆顶部落在离木杆底部
处,这根木杆原来的高度是
?.
9.
在
中,,,
.一只蜗牛从
点出发,以
的速度沿
的路径再回到
点,所需时间为
?
.
10.
如图所示是一段三级台阶,它的每一级的长、宽和高分别为
,,,
和
是这段台阶两个相对的端点.
点有一只蚂蚁,想到
点去吃可口的食物,设蚂蚁沿着台阶面爬到
点的最短路程为
,则以
为边长的正方形的面积为
?
.
11.
如图所示,将一根长为
的筷子置于底面直径为
,高为
的圆柱形茶杯中.设筷子露在茶杯外面的长为
(茶杯盛满水),则
的取值范围是
?.
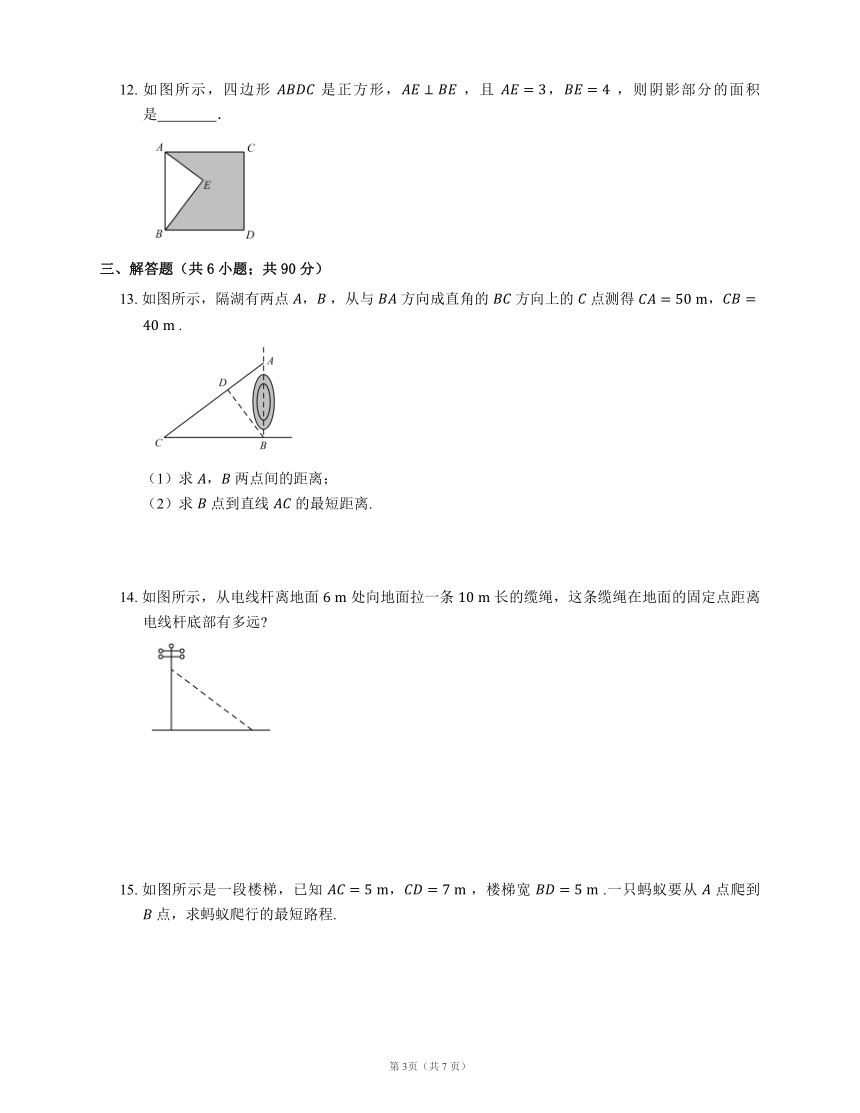
12.
如图所示,四边形
是正方形,
,且
,
,则阴影部分的面积是
?.
三、解答题(共6小题;共90分)
13.
如图所示,隔湖有两点
,
,从与
方向成直角的
方向上的
点测得
,
.
(1)求
,
两点间的距离;
(2)求
点到直线
的最短距离.
14.
如图所示,从电线杆离地面
处向地面拉一条
长的缆绳,这条缆绳在地面的固定点距离电线杆底部有多远?
15.
如图所示是一段楼梯,已知
,
,楼梯宽
.一只蚂蚁要从
点爬到
点,求蚂蚁爬行的最短路程.
16.
如图,梯子
斜靠在墙角上,
米,,求梯子的长.
17.
某公司举行开业一周年庆典,准备在一个长
,高
的台阶上铺设地毯(如图所示),已知台阶的宽为
.
(1)请你算一算共需购买多大面积的地毯;
(2)若地毯的价格为
,则购买地毯需花费多少元?
18.
如图,
中,,,
是
上一点,连接
.若
,,求
的长.
答案
1.
C
2.
B
3.
B
4.
A
5.
D
6.
B
7.
能
8.
9.
10.
11.
12.
13.
(1)
,
,
两点间的距离为
.
??????(2)
,
,
点到直线
的最短距离为
.
14.
15.
如图①
;
如图②、如图③
.
蚂蚁爬行的最短路程为
.
16.
米
17.
(1)
依题意,图中直角三角形一直角边长为
米,斜边长为
米,
根据勾股定理另一直角边长为
(米),
则需购买红地毯的长为
(米),
红地毯的宽则是台阶的宽,为
米,
所以面积是
(平方米).
??????(2)
(元),
答:则购买地毯需花费
元.
18.
设
,则
.
在
中,
,
,
,(舍去),
.
在
中,
,
.
第1页(共7
页)
勾股定理的应用
一、选择题(共6小题;共30分)
1.
如图所示,在一段高为
,长为
的楼梯表面铺地毯,则地毯的长度至少是
A.
B.
C.
D.
2.
如图所示,一架梯子长
,斜靠在—面墙上,梯子顶端离地面
.现要使梯子顶端离地面
,则梯子的底部在水平面方向上要向左滑动
A.
B.
C.
D.
3.
某住宅小区有一块草坪,如图所示,已知
,,,
,且
,则这块草坪的面积是
A.
B.
C.
D.
4.
如图所示,圆柱形玻璃杯的高为
,底面周长为
,在杯内离杯底
的点
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁离杯上沿
与蜂蜜相对的点
处,则蚂蚁到达蜂蜜的最短距离为
A.
B.
C.
D.
5.
一架
长的梯子斜立在一堵竖直的墙上,这时梯足距离墙底
.如果梯子的顶端沿墙下滑
,那么梯足将滑动
A.
B.
C.
D.
6.
如图所示是一棱长为
的正方体,把它分成
个小正方体,每个小正方体的边长都是
.如果一只蚂蚁从点
爬到点
,那么
,
间的最短距离
满足
A.
B.
C.
D.
或
二、填空题(共6小题;共30分)
7.
城墙高
,城墙外有—条宽为
的护城河,那么一架长为
的梯子能否跨过护城河到达城墙的顶端?答:
?(选填“能”或“不能”).
8.
如图所示,—根木杆在离地面
处断裂,木杆顶部落在离木杆底部
处,这根木杆原来的高度是
?.
9.
在
中,,,
.一只蜗牛从
点出发,以
的速度沿
的路径再回到
点,所需时间为
?
.
10.
如图所示是一段三级台阶,它的每一级的长、宽和高分别为
,,,
和
是这段台阶两个相对的端点.
点有一只蚂蚁,想到
点去吃可口的食物,设蚂蚁沿着台阶面爬到
点的最短路程为
,则以
为边长的正方形的面积为
?
.
11.
如图所示,将一根长为
的筷子置于底面直径为
,高为
的圆柱形茶杯中.设筷子露在茶杯外面的长为
(茶杯盛满水),则
的取值范围是
?.
12.
如图所示,四边形
是正方形,
,且
,
,则阴影部分的面积是
?.
三、解答题(共6小题;共90分)
13.
如图所示,隔湖有两点
,
,从与
方向成直角的
方向上的
点测得
,
.
(1)求
,
两点间的距离;
(2)求
点到直线
的最短距离.
14.
如图所示,从电线杆离地面
处向地面拉一条
长的缆绳,这条缆绳在地面的固定点距离电线杆底部有多远?
15.
如图所示是一段楼梯,已知
,
,楼梯宽
.一只蚂蚁要从
点爬到
点,求蚂蚁爬行的最短路程.
16.
如图,梯子
斜靠在墙角上,
米,,求梯子的长.
17.
某公司举行开业一周年庆典,准备在一个长
,高
的台阶上铺设地毯(如图所示),已知台阶的宽为
.
(1)请你算一算共需购买多大面积的地毯;
(2)若地毯的价格为
,则购买地毯需花费多少元?
18.
如图,
中,,,
是
上一点,连接
.若
,,求
的长.
答案
1.
C
2.
B
3.
B
4.
A
5.
D
6.
B
7.
能
8.
9.
10.
11.
12.
13.
(1)
,
,
两点间的距离为
.
??????(2)
,
,
点到直线
的最短距离为
.
14.
15.
如图①
;
如图②、如图③
.
蚂蚁爬行的最短路程为
.
16.
米
17.
(1)
依题意,图中直角三角形一直角边长为
米,斜边长为
米,
根据勾股定理另一直角边长为
(米),
则需购买红地毯的长为
(米),
红地毯的宽则是台阶的宽,为
米,
所以面积是
(平方米).
??????(2)
(元),
答:则购买地毯需花费
元.
18.
设
,则
.
在
中,
,
,
,(舍去),
.
在
中,
,
.
第1页(共7
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
