初数八上 知识点精讲 14.1.1-同底数幂的乘法(12张PPT)
文档属性
| 名称 | 初数八上 知识点精讲 14.1.1-同底数幂的乘法(12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览




文档简介
同底数幂的乘法
考点聚焦
1. 能理解同底数幂的乘法法则及运用;
2. 能掌握同底数幂乘法法则的逆运算.
知识梳理
考点一 同底数幂的乘法法则
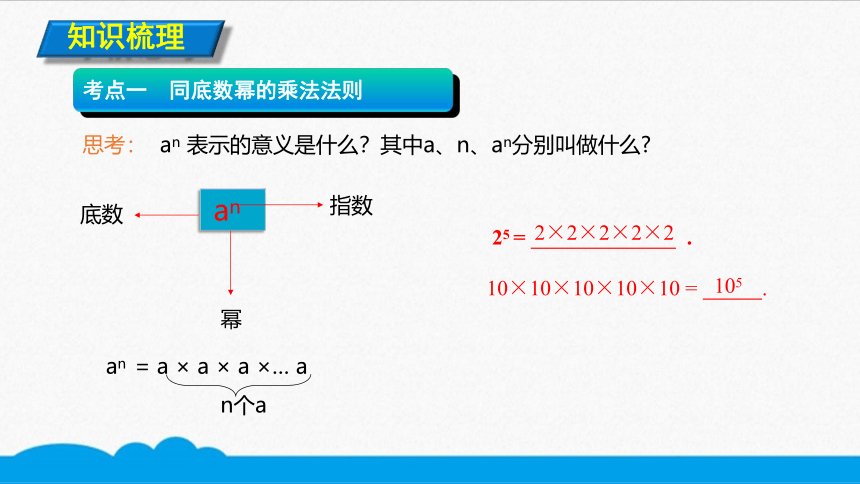
思考: an 表示的意义是什么?其中a、n、an分别叫做什么?
an
底数
幂
指数
an = a × a × a ×… a
n个a
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
知识梳理
考点一 同底数幂的乘法法则
请同学们先根据自己的理解,解答下列各题.
23 ×22 = =2( )
5
(2×2×2)×(2×2)
a3×a2 = =a( ) .
5
(a· a· a)
(a· a)
3个a
2个a
·
猜想: am · an= ? (当m、n都是正整数)
知识梳理
考点一 同底数幂的乘法法则
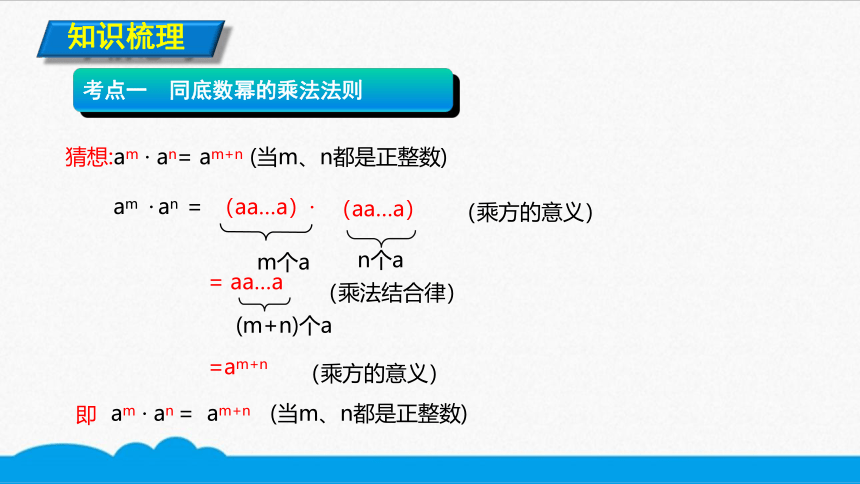
猜想:am · an= am+n (当m、n都是正整数)
am · an =
m个a
n个a
(aa…a)·
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
知识梳理
考点一 同底数幂的乘法法则
am·an =am+n (当m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
1.同底数幂的乘法性质:
运算形式
运算方法
(同底、乘法)
(底不变、指加法)
2.三个以上同底数幂相乘时,也具有这一性质:
(m,n,p都是正整数)
典例剖析
①单个字母或数字的指数为1;
②底数为负数时要加括号;
?计算时要先观察底数是否相同,不同底的要先化为同底的才可以运用法则.
方法点拨
(1)????·????6
?
解:原式=????1+6
= ????7
?
(2)(?2)×(?2)2×(?2)3
?
解:原式=(?2)1+2+3
= (?2)6
= 26
?
(3)100×10????×10?????2
?
解:原式= 102 ×10????×10?????2
= 102+????+(?????2)
= 102????
?
知识梳理
考点二 同底数幂乘法法则的逆运算
am·an =am+n (m、n都是正整数)
同底数幂的乘法性质:
逆运算:
am+n =am·an (m、n都是正整数)
看到指数相加的式子,要能想到同底数幂乘法的逆运算.
方法点拨
典例剖析
已知:am=2, an=3.求am+n =__________.
解: am+n = am · an (逆运算)
=2 × 3
=6
6
备考技法
1.同底数幂相乘,底数不变,指数相加.
对这个法则要注重理解“同底,相乘,不变,相加”这八个字.
2.底数可以是一个数,也可以是单项式或多项式.
运算时不同底的要先化为同底的,才可以运用法则.
4.解题时,要注意指数为1的情况,不要漏掉.
3.解题时,底数是负数的要用括号把底数括起来.
5.灵活运用公式,看到指数相加的式子,要能想到同底数幂乘法的逆运算.
同底数幂的乘法
思维导图
底数不变,指数相加
am · an = am+n (m、n正整数)
元申小课 必有收获
考点聚焦
1. 能理解同底数幂的乘法法则及运用;
2. 能掌握同底数幂乘法法则的逆运算.
知识梳理
考点一 同底数幂的乘法法则
思考: an 表示的意义是什么?其中a、n、an分别叫做什么?
an
底数
幂
指数
an = a × a × a ×… a
n个a
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
知识梳理
考点一 同底数幂的乘法法则
请同学们先根据自己的理解,解答下列各题.
23 ×22 = =2( )
5
(2×2×2)×(2×2)
a3×a2 = =a( ) .
5
(a· a· a)
(a· a)
3个a
2个a
·
猜想: am · an= ? (当m、n都是正整数)
知识梳理
考点一 同底数幂的乘法法则
猜想:am · an= am+n (当m、n都是正整数)
am · an =
m个a
n个a
(aa…a)·
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
知识梳理
考点一 同底数幂的乘法法则
am·an =am+n (当m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
1.同底数幂的乘法性质:
运算形式
运算方法
(同底、乘法)
(底不变、指加法)
2.三个以上同底数幂相乘时,也具有这一性质:
(m,n,p都是正整数)
典例剖析
①单个字母或数字的指数为1;
②底数为负数时要加括号;
?计算时要先观察底数是否相同,不同底的要先化为同底的才可以运用法则.
方法点拨
(1)????·????6
?
解:原式=????1+6
= ????7
?
(2)(?2)×(?2)2×(?2)3
?
解:原式=(?2)1+2+3
= (?2)6
= 26
?
(3)100×10????×10?????2
?
解:原式= 102 ×10????×10?????2
= 102+????+(?????2)
= 102????
?
知识梳理
考点二 同底数幂乘法法则的逆运算
am·an =am+n (m、n都是正整数)
同底数幂的乘法性质:
逆运算:
am+n =am·an (m、n都是正整数)
看到指数相加的式子,要能想到同底数幂乘法的逆运算.
方法点拨
典例剖析
已知:am=2, an=3.求am+n =__________.
解: am+n = am · an (逆运算)
=2 × 3
=6
6
备考技法
1.同底数幂相乘,底数不变,指数相加.
对这个法则要注重理解“同底,相乘,不变,相加”这八个字.
2.底数可以是一个数,也可以是单项式或多项式.
运算时不同底的要先化为同底的,才可以运用法则.
4.解题时,要注意指数为1的情况,不要漏掉.
3.解题时,底数是负数的要用括号把底数括起来.
5.灵活运用公式,看到指数相加的式子,要能想到同底数幂乘法的逆运算.
同底数幂的乘法
思维导图
底数不变,指数相加
am · an = am+n (m、n正整数)
元申小课 必有收获
