初数九上 知识点精讲 24.1.2-垂径定理及其应用(共10张PPT)
文档属性
| 名称 | 初数九上 知识点精讲 24.1.2-垂径定理及其应用(共10张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 948.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览


文档简介
垂径定理及其应用
考点聚焦
1.理解垂径定理及其推论
2.能利用垂径定理解决实际问题
考点一 垂径定理
知识梳理
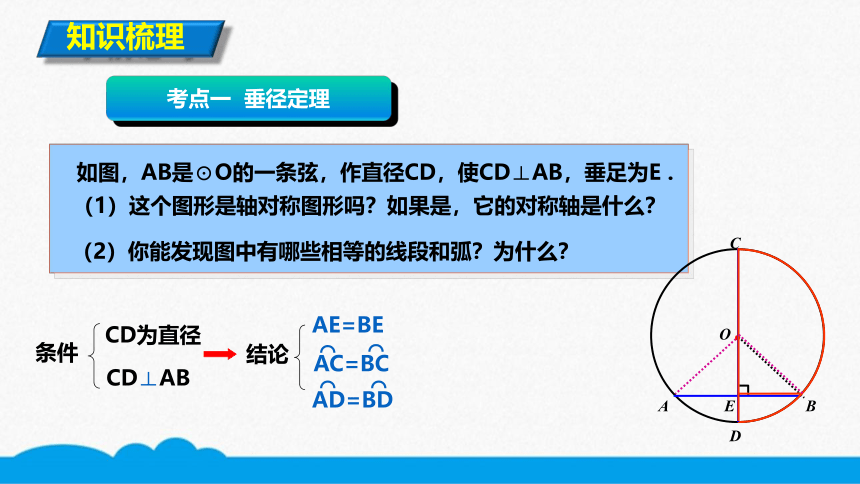
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E .
(2)你能发现图中有哪些相等的线段和弧?为什么?
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
条件
CD为直径
CD⊥AB
结论
AE=BE
AC=BC
⌒
⌒
AD=BD
⌒
⌒
O
A
B
C
D
E
·
知识梳理
考点一 垂径定理
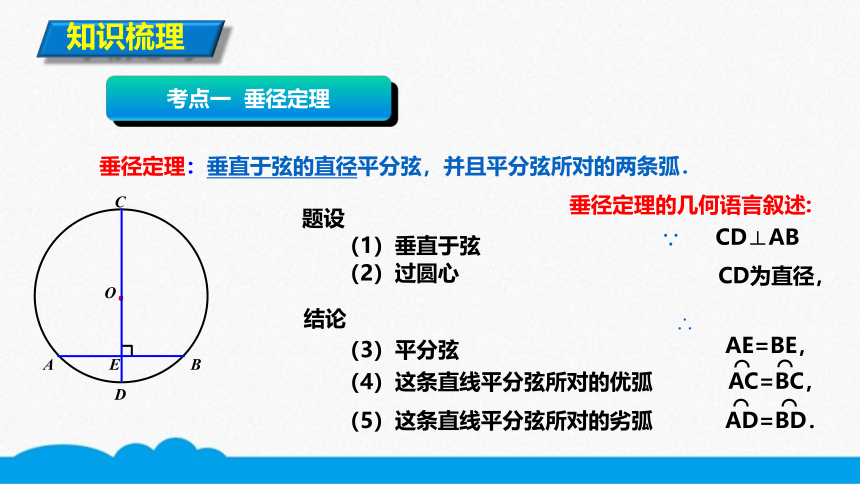
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
题设
(1)垂直于弦
(2)过圆心
结论
(3)平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
垂径定理的几何语言叙述:
AE=BE,
AC=BC,
⌒
⌒
AD=BD.
⌒
⌒
∴
∵
CD⊥AB
CD为直径,
·
O
A
B
C
D
E
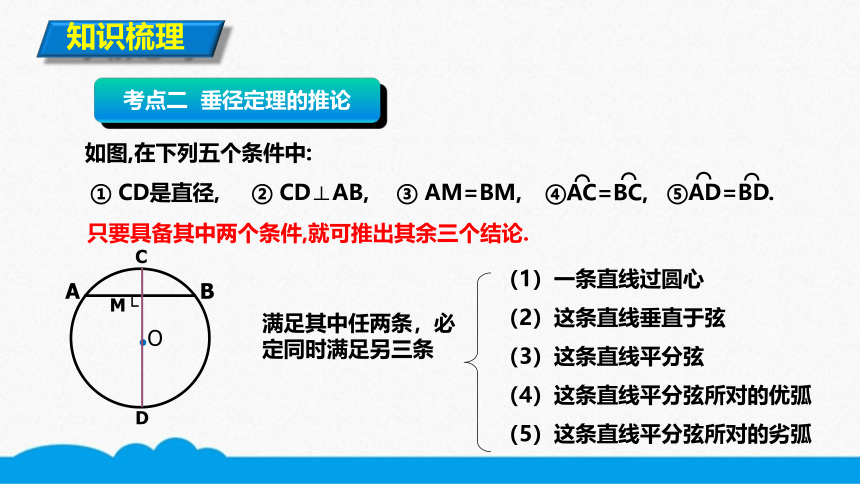
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
考点二 垂径定理的推论
知识梳理
●O
A
B
C
D
M└
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
典例剖析
判断下列图形,能否使用垂径定理?
×
√
×
√
√
√
解决有关弦的问题时,经常连接半径;过圆心作一条与弦垂直的线段等辅助线,为应用垂径定理创造条件。
垂径定理经常和勾股定理结合使用。
方法点拨
典例剖析
弓形的弦长AB为24cm,弓形的高CD为8cm,则这弓形所在圆的半径为 .
12
8
13cm
解:设半径为r,则OD=r-8,BD=12cm
在Rt△OBD中,????????????= ????????????+ ????????????
∴ ????????= ????????????+ (?????????)????
解得:r=13cm
?
备考技巧
E
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
思维导图
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
垂径定理的推论:
元申小课 必有收获
考点聚焦
1.理解垂径定理及其推论
2.能利用垂径定理解决实际问题
考点一 垂径定理
知识梳理
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E .
(2)你能发现图中有哪些相等的线段和弧?为什么?
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
条件
CD为直径
CD⊥AB
结论
AE=BE
AC=BC
⌒
⌒
AD=BD
⌒
⌒
O
A
B
C
D
E
·
知识梳理
考点一 垂径定理
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
题设
(1)垂直于弦
(2)过圆心
结论
(3)平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
垂径定理的几何语言叙述:
AE=BE,
AC=BC,
⌒
⌒
AD=BD.
⌒
⌒
∴
∵
CD⊥AB
CD为直径,
·
O
A
B
C
D
E
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
考点二 垂径定理的推论
知识梳理
●O
A
B
C
D
M└
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
典例剖析
判断下列图形,能否使用垂径定理?
×
√
×
√
√
√
解决有关弦的问题时,经常连接半径;过圆心作一条与弦垂直的线段等辅助线,为应用垂径定理创造条件。
垂径定理经常和勾股定理结合使用。
方法点拨
典例剖析
弓形的弦长AB为24cm,弓形的高CD为8cm,则这弓形所在圆的半径为 .
12
8
13cm
解:设半径为r,则OD=r-8,BD=12cm
在Rt△OBD中,????????????= ????????????+ ????????????
∴ ????????= ????????????+ (?????????)????
解得:r=13cm
?
备考技巧
E
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
思维导图
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
垂径定理的推论:
元申小课 必有收获
同课章节目录
