初数九上 知识点精讲 24.1.4-圆周角定理(共15张PPT)
文档属性
| 名称 | 初数九上 知识点精讲 24.1.4-圆周角定理(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览




文档简介
圆周角定理
考点聚焦
1. 能理解圆周角定理及推论;
2. 能应用圆周角定理解决实际问题.
知识梳理
考点一 圆周角定理
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
连接AO,BO,得到圆心角∠AOB,
可以发现:
∠ACB 和∠AOB 对着______
AB
)
O
r
0
B
A
C
知识梳理
问题1:∠ACB 和∠AOB之间存在什么关系呢?分别测量它们的度数,试着猜想它们之间的关系,运用所学知识证明你的结论.
O
r
0
B
A
C
∠ACB=______∠AOB
经过测量我们发现:
2
1
猜想:同弧所对的圆周角等于这条弧所对圆心角度数的一半.
考点一 圆周角定理
知识梳理
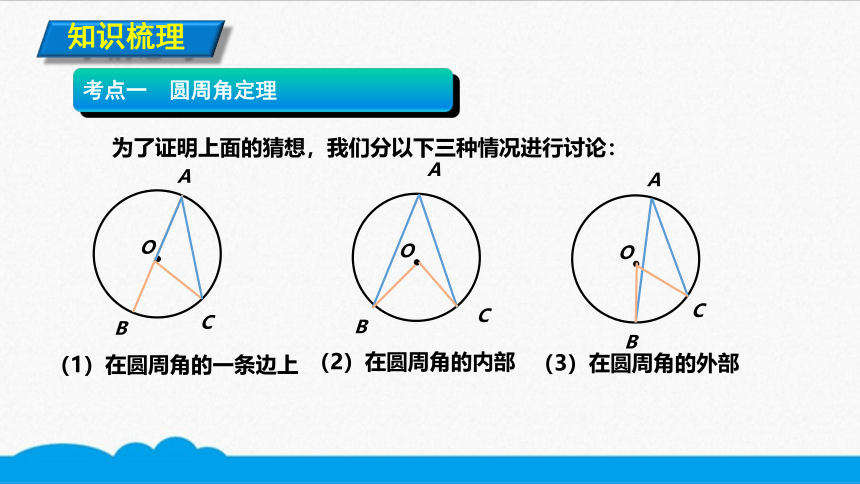
为了证明上面的猜想,我们分以下三种情况进行讨论:
(1)在圆周角的一条边上
(2)在圆周角的内部
(3)在圆周角的外部
O
B
A
C
O
B
A
C
O
B
A
C
考点一 圆周角定理
知识梳理
考点一 圆周角定理
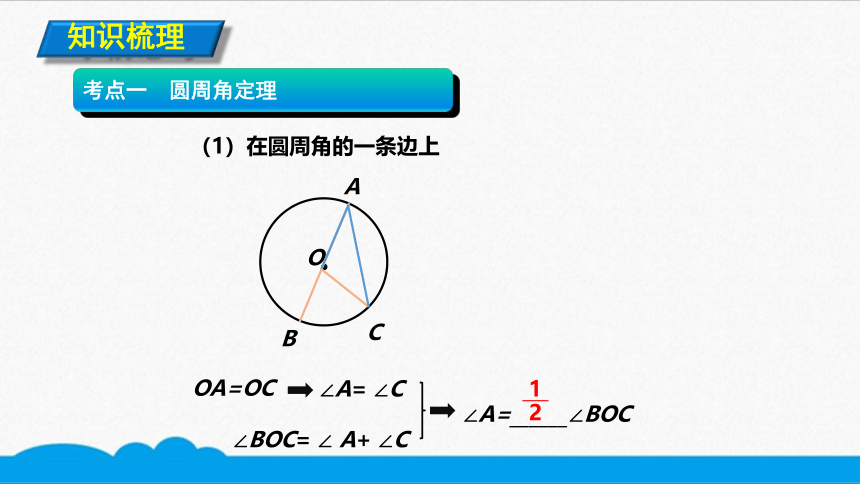
(1)在圆周角的一条边上
O
B
A
C
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
∠A=______∠BOC
2
1
知识梳理
考点一 圆周角定理
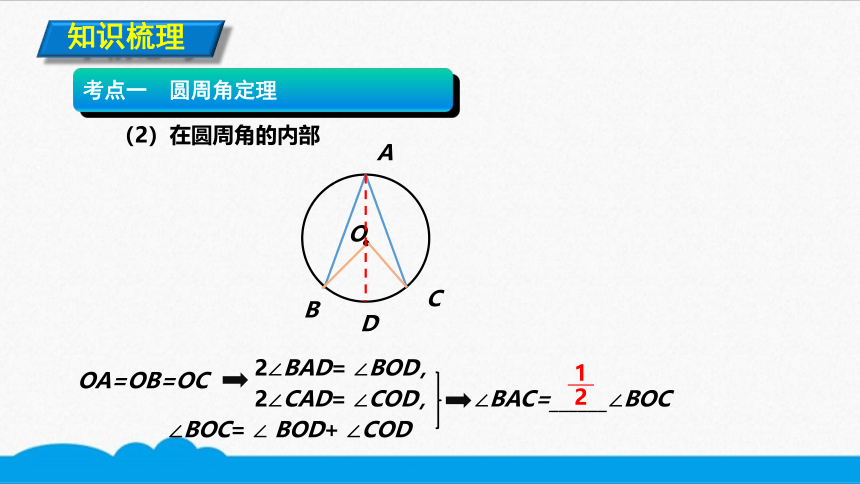
(2)在圆周角的内部
O
B
A
C
D
OA=OB=OC
2∠BAD= ∠BOD,
2∠CAD= ∠COD,
∠BOC= ∠ BOD+ ∠COD
∠BAC=______∠BOC
2
1
知识梳理
考点一 圆周角定理
(3)在圆周角的外部
O
B
A
C
D
OA=OB=OC
∠DOB=2∠OAB
∠DOC=2∠OAC
∠BOC= ∠ DOC- ∠DOB
∠BAC=______∠BOC
2
1
知识梳理
考点一 圆周角定理
圆周角定理:
一条弧所对的圆周角等于该弧它所对的_______的______.
O
0
B
A
C
一半
圆心角
典例剖析
练一练:下列四个图中,∠x是圆周角的是( )
C
知识梳理
考点二 圆周角定理的推论
问题1:根据圆周角定理,结合已经学习过的有关圆的知识,我们还能得到哪些推论?
O
B
A
C
推论一:同弧或等弧所对的圆周角相等.
推论二:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
O
A
B
C1
C3
C2
典例剖析
例 如图,⊙O 的直径AB 为10cm,弦AC 为6cm.∠ACB的平分线交于点D,求BC,AD,BD 的长.
O
A
B
C
D
解 如图,连接OD.
∵AB是直径,
∴ ∠ACB=∠ADB=90°.
在Rt△ABC 中,
BC=?????????????????????????=?????????????????????=8
?
典例剖析
例 如图,⊙O 的直径AB 为10cm,弦AC为6cm.∠ACB的平分线交于点D,求BC,AD,BD 的长.
∴∠ACD=∠BCD.
∵CD平分∠ACB,
∴∠AOD=∠BOD.
∴AD=BD.
又在Rt△ABD 中,
∴AD 2+BD 2=AB 2.
∴AD=BD=????????AB= ????????×10=5???? cm
?
O
A
B
C
D
思维导图
圆周角
圆周角定理的推论
圆周角定理
一条弧所对的圆周角等于该弧它所对的圆心角的一半;
推论一:同弧或等弧所对的圆周角相等.
推论二:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
元申小课 必有收获
考点聚焦
1. 能理解圆周角定理及推论;
2. 能应用圆周角定理解决实际问题.
知识梳理
考点一 圆周角定理
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
连接AO,BO,得到圆心角∠AOB,
可以发现:
∠ACB 和∠AOB 对着______
AB
)
O
r
0
B
A
C
知识梳理
问题1:∠ACB 和∠AOB之间存在什么关系呢?分别测量它们的度数,试着猜想它们之间的关系,运用所学知识证明你的结论.
O
r
0
B
A
C
∠ACB=______∠AOB
经过测量我们发现:
2
1
猜想:同弧所对的圆周角等于这条弧所对圆心角度数的一半.
考点一 圆周角定理
知识梳理
为了证明上面的猜想,我们分以下三种情况进行讨论:
(1)在圆周角的一条边上
(2)在圆周角的内部
(3)在圆周角的外部
O
B
A
C
O
B
A
C
O
B
A
C
考点一 圆周角定理
知识梳理
考点一 圆周角定理
(1)在圆周角的一条边上
O
B
A
C
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
∠A=______∠BOC
2
1
知识梳理
考点一 圆周角定理
(2)在圆周角的内部
O
B
A
C
D
OA=OB=OC
2∠BAD= ∠BOD,
2∠CAD= ∠COD,
∠BOC= ∠ BOD+ ∠COD
∠BAC=______∠BOC
2
1
知识梳理
考点一 圆周角定理
(3)在圆周角的外部
O
B
A
C
D
OA=OB=OC
∠DOB=2∠OAB
∠DOC=2∠OAC
∠BOC= ∠ DOC- ∠DOB
∠BAC=______∠BOC
2
1
知识梳理
考点一 圆周角定理
圆周角定理:
一条弧所对的圆周角等于该弧它所对的_______的______.
O
0
B
A
C
一半
圆心角
典例剖析
练一练:下列四个图中,∠x是圆周角的是( )
C
知识梳理
考点二 圆周角定理的推论
问题1:根据圆周角定理,结合已经学习过的有关圆的知识,我们还能得到哪些推论?
O
B
A
C
推论一:同弧或等弧所对的圆周角相等.
推论二:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
O
A
B
C1
C3
C2
典例剖析
例 如图,⊙O 的直径AB 为10cm,弦AC 为6cm.∠ACB的平分线交于点D,求BC,AD,BD 的长.
O
A
B
C
D
解 如图,连接OD.
∵AB是直径,
∴ ∠ACB=∠ADB=90°.
在Rt△ABC 中,
BC=?????????????????????????=?????????????????????=8
?
典例剖析
例 如图,⊙O 的直径AB 为10cm,弦AC为6cm.∠ACB的平分线交于点D,求BC,AD,BD 的长.
∴∠ACD=∠BCD.
∵CD平分∠ACB,
∴∠AOD=∠BOD.
∴AD=BD.
又在Rt△ABD 中,
∴AD 2+BD 2=AB 2.
∴AD=BD=????????AB= ????????×10=5???? cm
?
O
A
B
C
D
思维导图
圆周角
圆周角定理的推论
圆周角定理
一条弧所对的圆周角等于该弧它所对的圆心角的一半;
推论一:同弧或等弧所对的圆周角相等.
推论二:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
元申小课 必有收获
同课章节目录
