初数九上 知识点精讲 22.1.1 二次函数的定义、图象与性质(共10张PPT)
文档属性
| 名称 | 初数九上 知识点精讲 22.1.1 二次函数的定义、图象与性质(共10张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 671.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览




文档简介
二次函数定义、
图象与性质
考点聚焦
1. 重点:二次函数的定义、图象与性质;
2. 难点:二次函数的图象与性质。
二次函数的定义:
知识梳理
考点一 二次函数的定义
形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.其中x是自变量,a,b,c分别是二次项系数、一次项系数和常数项.
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
注意:
二次函数的一般形式:
知识梳理
考点一 二次函数的定义
y=ax2+bx+c(a ≠0,a,b,c是常数)
y=ax2;
y=ax2+bx;
y=ax2+c(a ≠0,a,b,c是常数).
特殊形式:
典例剖析
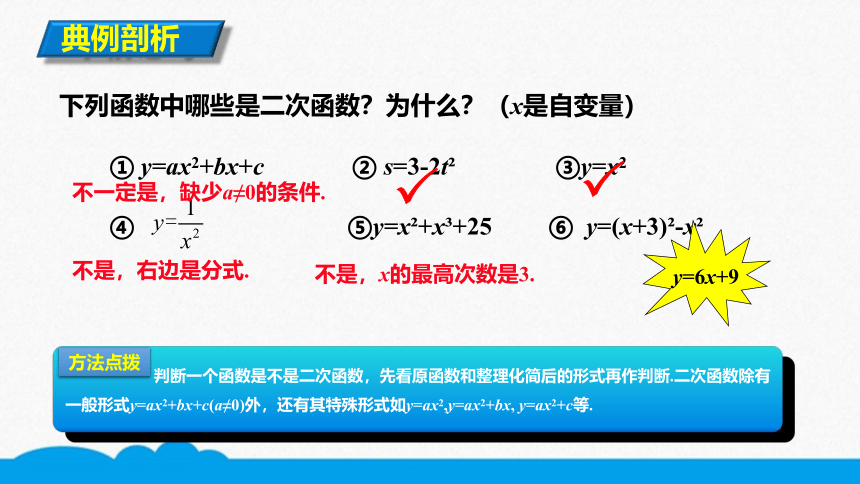
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
方法点拨
下列函数中哪些是二次函数?为什么?(x是自变量)
① y=ax2+bx+c ② s=3-2t? ③y=x2
④ ⑤y=x?+x?+25 ⑥ y=(x+3)?-x?
不一定是,缺少a≠0的条件.
不是,右边是分式.
不是,x的最高次数是3.
y=6x+9
二次函数y=ax2+bx+c的图象和性质:
知识梳理
考点二 二次函数的图象与性质
图象是抛物线,a>0,开口向上,a<0,开口向下;
顶点坐标是:
对称轴是:直线
一般地,二次函数
二次函数y=ax2+bx+c的图象和性质:
知识梳理
考点二 二次函数的图象与性质
x
y
O
x
y
O
如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大.
如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小.
典例剖析
根据解析式中字母系数,判断抛物线的开口方向和对称轴及增减变化,最后判断系数的取值范围。熟练掌握二次函数的性质是解题关键。
方法点拨
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧或与直线x=1重合,而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
D
备考技法
1、二次函数的定义:
形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.
2、二次函数的图象与性质:
图象是抛物线,a决定开口方向,
顶点、对称轴、增减性对于正确认识二次函数的图象性质起着关键性作用。
二次函数
二次函数图象是抛物线
形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。
思维导图
二次函数图象的开口
方向、对称轴、顶点等
是分析问题的关键。
图象与性质
考点聚焦
1. 重点:二次函数的定义、图象与性质;
2. 难点:二次函数的图象与性质。
二次函数的定义:
知识梳理
考点一 二次函数的定义
形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.其中x是自变量,a,b,c分别是二次项系数、一次项系数和常数项.
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
注意:
二次函数的一般形式:
知识梳理
考点一 二次函数的定义
y=ax2+bx+c(a ≠0,a,b,c是常数)
y=ax2;
y=ax2+bx;
y=ax2+c(a ≠0,a,b,c是常数).
特殊形式:
典例剖析
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
方法点拨
下列函数中哪些是二次函数?为什么?(x是自变量)
① y=ax2+bx+c ② s=3-2t? ③y=x2
④ ⑤y=x?+x?+25 ⑥ y=(x+3)?-x?
不一定是,缺少a≠0的条件.
不是,右边是分式.
不是,x的最高次数是3.
y=6x+9
二次函数y=ax2+bx+c的图象和性质:
知识梳理
考点二 二次函数的图象与性质
图象是抛物线,a>0,开口向上,a<0,开口向下;
顶点坐标是:
对称轴是:直线
一般地,二次函数
二次函数y=ax2+bx+c的图象和性质:
知识梳理
考点二 二次函数的图象与性质
x
y
O
x
y
O
如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大.
如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小.
典例剖析
根据解析式中字母系数,判断抛物线的开口方向和对称轴及增减变化,最后判断系数的取值范围。熟练掌握二次函数的性质是解题关键。
方法点拨
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧或与直线x=1重合,而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
D
备考技法
1、二次函数的定义:
形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.
2、二次函数的图象与性质:
图象是抛物线,a决定开口方向,
顶点、对称轴、增减性对于正确认识二次函数的图象性质起着关键性作用。
二次函数
二次函数图象是抛物线
形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。
思维导图
二次函数图象的开口
方向、对称轴、顶点等
是分析问题的关键。
同课章节目录
