初数九上 知识点精讲 22.2.3 点的坐标及坐标与图像性质(共9张PPT)
文档属性
| 名称 | 初数九上 知识点精讲 22.2.3 点的坐标及坐标与图像性质(共9张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 729.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览



文档简介
点的坐标及
坐标与图形性质
考点聚焦
1. 重点:两点关于原点对称时的坐标符号及作关于原点对称的图形;
2. 难点:利用平面直角坐标系培养学生数形结合的数学思想。
关于原点对称的点的坐标规律:
知识梳理
考点一 关于原点对称的点的坐标及图形性质
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为点P′(-x,-y).
找关于原点对称的点,本质上是对称中心为原点的中心对称作图,故也可采用中心对称作图的方法确定对称点.
注意:
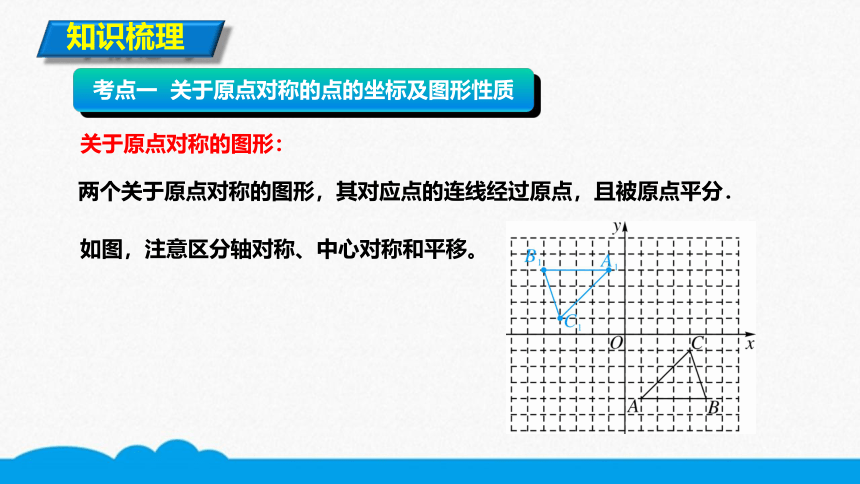
关于原点对称的图形:
知识梳理
考点一 关于原点对称的点的坐标及图形性质
两个关于原点对称的图形,其对应点的连线经过原点,且被原点平分.
如图,注意区分轴对称、中心对称和平移。
若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,
则m+n的值是( )
A.1 B.-3 C.5 D.-7
典例剖析
根据关于原点对称的点的坐标符号相反计算字母m,n的值再求和。
方法点拨
C
点的坐标符号相反
m-1=-3,m=-2;
2-n=-5,n=7。
典例剖析
已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点的坐标为(2, ),则B点与D点的坐标分别为( ) A.(-2, ),(2,- ) B.(- ,2),( ,-2) C.(- ,2),(2,- ) D.(- , )( ,- )
典例剖析
根据正方形的性质证明△AFO≌△OED,计算点D的坐标,再利用中心对称的性质写出点B坐标。
方法点拨
解:如图,连接OA,OD,过点A作AF⊥x轴于点F,过点D作DE⊥x轴于点E.
易证△AFO≌△OED,
∴OE=AF= ,DE=OF=2.
∴D( ,-2).
∵B,D关于原点对称,∴B(- ,2).
备考技法
1、关于原点对称的点的坐标规律:
(两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为点P′(-x,-y).
2、关于原点对称的图形:
找关于原点对称的点,本质上是对称中心为原点的中心对称作图,故也可采用中心对称作图的方法确定对称点.
点的坐标及图形性质
关于原点对称的图形
关于原点对称的点
的坐标规律。
思维导图
点的坐标规律及图形性质
以原点为对称中心
坐标与图形性质
考点聚焦
1. 重点:两点关于原点对称时的坐标符号及作关于原点对称的图形;
2. 难点:利用平面直角坐标系培养学生数形结合的数学思想。
关于原点对称的点的坐标规律:
知识梳理
考点一 关于原点对称的点的坐标及图形性质
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为点P′(-x,-y).
找关于原点对称的点,本质上是对称中心为原点的中心对称作图,故也可采用中心对称作图的方法确定对称点.
注意:
关于原点对称的图形:
知识梳理
考点一 关于原点对称的点的坐标及图形性质
两个关于原点对称的图形,其对应点的连线经过原点,且被原点平分.
如图,注意区分轴对称、中心对称和平移。
若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,
则m+n的值是( )
A.1 B.-3 C.5 D.-7
典例剖析
根据关于原点对称的点的坐标符号相反计算字母m,n的值再求和。
方法点拨
C
点的坐标符号相反
m-1=-3,m=-2;
2-n=-5,n=7。
典例剖析
已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点的坐标为(2, ),则B点与D点的坐标分别为( ) A.(-2, ),(2,- ) B.(- ,2),( ,-2) C.(- ,2),(2,- ) D.(- , )( ,- )
典例剖析
根据正方形的性质证明△AFO≌△OED,计算点D的坐标,再利用中心对称的性质写出点B坐标。
方法点拨
解:如图,连接OA,OD,过点A作AF⊥x轴于点F,过点D作DE⊥x轴于点E.
易证△AFO≌△OED,
∴OE=AF= ,DE=OF=2.
∴D( ,-2).
∵B,D关于原点对称,∴B(- ,2).
备考技法
1、关于原点对称的点的坐标规律:
(两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为点P′(-x,-y).
2、关于原点对称的图形:
找关于原点对称的点,本质上是对称中心为原点的中心对称作图,故也可采用中心对称作图的方法确定对称点.
点的坐标及图形性质
关于原点对称的图形
关于原点对称的点
的坐标规律。
思维导图
点的坐标规律及图形性质
以原点为对称中心
同课章节目录
