初数七年级 专题5 有理数的加减(共19张PPT)
文档属性
| 名称 | 初数七年级 专题5 有理数的加减(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览






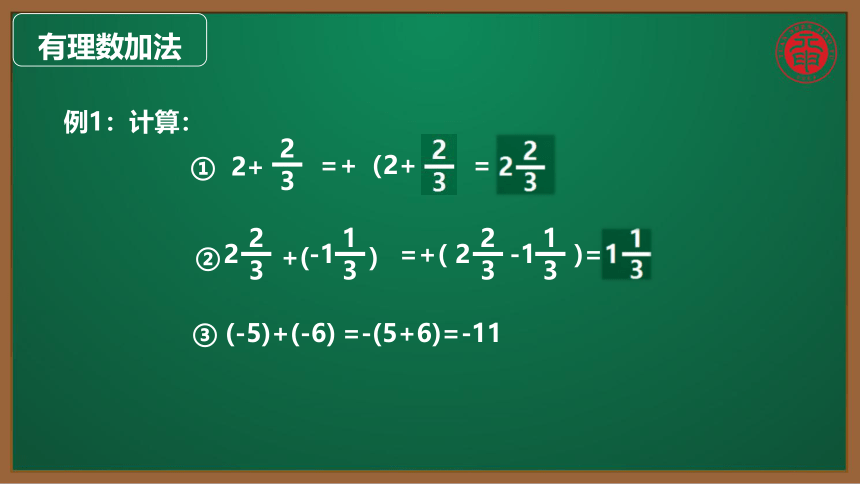
文档简介
有 理 数 的 加 减
有 理 数 的 加 法 法则:
1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值;互为相反数的两个数相
加得0.
3、一个数与0相加仍得这个数。
有理数加法
有理数加法法则(分类讨论思想)
(1)同号两数相加:
分两步:先定号,再定值
与加数符号相同
加数绝对值相加
并把绝对值相加
取相同的符号,
如: (+11)+(+12)=
+
+
( )
11
12
+
=+23
如: (-11)+(-12)=
-
-
( )
11
12
+
=-23
有理数加法
有理数加法法则(分类讨论思想)
(2)异号两数相加:
分两步:先定号,再定值
与绝对值大的符号相同
加数绝对值大的减小的
并用较大的绝对值减去较小的绝对值
取绝对值较大的加数符号,
如: (-14)+(+7)=
-
-
14
7
=-7
( )
有理数加法
有理数加法法则(分类讨论思想)
(3)一个数与0相加:
仍得这个数
如: 14+0=
14
-10+0=-10
0+0=0
有理数加法
例1:计算:
① 2+
② +( )
2
3
-1
1
3
2
2
3
=+(2+ )=
③ (-5)+(-6)
=+( )=
2
2
3
-1
1
3
=-(5+6)=-11
有理数加法
例2: 填空
① 若|a|=3,|b|=2,a<b,则a+b=_________.
② 已知两数的和为正,下面判断中,正确的是( )
A. 两个加数必须都是正数
B. 两个加数都必须是负数
C. 两个加数至少有一个是正数
D. 两个加数必须是一正一负
③ 若|a+1|与|b+3|互为相反数,则a=___,b=___.
-1或-5
C
-1
-3
有理数加法
正数+正数
正数(绝对值较大)+负数
正数+0
|a+1|+|b+3|=0
例3:① 若|a|=4,|b|=3,若ab同号,则a+b=_________.
② 两个有理数的和小于每一个加数,那么这两个数( )
A. 都是正数 B. 都是负数
C. 一正一负 D. 有一个加数为0
因为|a|=4,|b|=3,
所以a=?4,b=?3;
因为ab同号,
所以a=+3,b=+4
或a=-3,b=-4
?7
B
有理数加法
例4:① 若|a|=7,|b|=5,a<b,则a+b=_________.
② 两个有理数的和为负数,那么这两个数( )
A. 都是负数 B. 没有负数
C. 必有一个为0 D. 至少有一个负数
-2,-12
D
有理数加法
有 理 数 的 减 法
有理数减法法则(化归思想)
减去一个数,等于加上这个数的相反数
如: (-14)-(+7)=
同时改变两个符号:
(1)运算符号,减号变加号
(2)性质符号,减数变成它的相反数
+(-7)=-21
-
-14
有理数减法
加减混合运算——(化归思想)
利用减法的化归思想,遇到加减混合运算时,
只需要把所有的减法都化成加法!
如:19+(-1.8)-(-89)+(-5.1)-27+(-1.1)-(-4.8)
变成:19+(-1.8)+89+(-5.1)-27+(-1.1)+4.8
再求所有有理数的代数和即可!
有理数减法
例5: (1)6-(-3)
(2)-1-2
(3)12-(+18)-(+23)
=6+3=9
=-1+(-2)=-3
=12+(-18)+(-23)
=-29
有理数减法
(2) (-7)+|-31|-21+(-4)
例6:(1) 1+(-12)-(-9)+(-10)
=1-12+9-10
=10-22
=1+9-12-10
=-12
=-7+31-21-4
=-7-21-4+31
=-32+31
=-1
有理数减法
例7:设a是最大的负整数,b是最小的正整数,|c|=2,
则a-b+c=______________.
答案
0或-4
a=-1
b=1
c=?2
当c=2时,
a-b+c=-1-1+2
=0
当c=-2时,
a-b+c=-1-1+(-2)
=-4
有理数减法
小结
有 理 数 的 加 法 法则:
1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值;互为相反数的两个数相
加得0.
3、一个数与0相加仍得这个数。
有理数减法法则:
减去一个数,等于加上这个数的相反数
谢谢观看
有 理 数 的 加 法 法则:
1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值;互为相反数的两个数相
加得0.
3、一个数与0相加仍得这个数。
有理数加法
有理数加法法则(分类讨论思想)
(1)同号两数相加:
分两步:先定号,再定值
与加数符号相同
加数绝对值相加
并把绝对值相加
取相同的符号,
如: (+11)+(+12)=
+
+
( )
11
12
+
=+23
如: (-11)+(-12)=
-
-
( )
11
12
+
=-23
有理数加法
有理数加法法则(分类讨论思想)
(2)异号两数相加:
分两步:先定号,再定值
与绝对值大的符号相同
加数绝对值大的减小的
并用较大的绝对值减去较小的绝对值
取绝对值较大的加数符号,
如: (-14)+(+7)=
-
-
14
7
=-7
( )
有理数加法
有理数加法法则(分类讨论思想)
(3)一个数与0相加:
仍得这个数
如: 14+0=
14
-10+0=-10
0+0=0
有理数加法
例1:计算:
① 2+
② +( )
2
3
-1
1
3
2
2
3
=+(2+ )=
③ (-5)+(-6)
=+( )=
2
2
3
-1
1
3
=-(5+6)=-11
有理数加法
例2: 填空
① 若|a|=3,|b|=2,a<b,则a+b=_________.
② 已知两数的和为正,下面判断中,正确的是( )
A. 两个加数必须都是正数
B. 两个加数都必须是负数
C. 两个加数至少有一个是正数
D. 两个加数必须是一正一负
③ 若|a+1|与|b+3|互为相反数,则a=___,b=___.
-1或-5
C
-1
-3
有理数加法
正数+正数
正数(绝对值较大)+负数
正数+0
|a+1|+|b+3|=0
例3:① 若|a|=4,|b|=3,若ab同号,则a+b=_________.
② 两个有理数的和小于每一个加数,那么这两个数( )
A. 都是正数 B. 都是负数
C. 一正一负 D. 有一个加数为0
因为|a|=4,|b|=3,
所以a=?4,b=?3;
因为ab同号,
所以a=+3,b=+4
或a=-3,b=-4
?7
B
有理数加法
例4:① 若|a|=7,|b|=5,a<b,则a+b=_________.
② 两个有理数的和为负数,那么这两个数( )
A. 都是负数 B. 没有负数
C. 必有一个为0 D. 至少有一个负数
-2,-12
D
有理数加法
有 理 数 的 减 法
有理数减法法则(化归思想)
减去一个数,等于加上这个数的相反数
如: (-14)-(+7)=
同时改变两个符号:
(1)运算符号,减号变加号
(2)性质符号,减数变成它的相反数
+(-7)=-21
-
-14
有理数减法
加减混合运算——(化归思想)
利用减法的化归思想,遇到加减混合运算时,
只需要把所有的减法都化成加法!
如:19+(-1.8)-(-89)+(-5.1)-27+(-1.1)-(-4.8)
变成:19+(-1.8)+89+(-5.1)-27+(-1.1)+4.8
再求所有有理数的代数和即可!
有理数减法
例5: (1)6-(-3)
(2)-1-2
(3)12-(+18)-(+23)
=6+3=9
=-1+(-2)=-3
=12+(-18)+(-23)
=-29
有理数减法
(2) (-7)+|-31|-21+(-4)
例6:(1) 1+(-12)-(-9)+(-10)
=1-12+9-10
=10-22
=1+9-12-10
=-12
=-7+31-21-4
=-7-21-4+31
=-32+31
=-1
有理数减法
例7:设a是最大的负整数,b是最小的正整数,|c|=2,
则a-b+c=______________.
答案
0或-4
a=-1
b=1
c=?2
当c=2时,
a-b+c=-1-1+2
=0
当c=-2时,
a-b+c=-1-1+(-2)
=-4
有理数减法
小结
有 理 数 的 加 法 法则:
1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值;互为相反数的两个数相
加得0.
3、一个数与0相加仍得这个数。
有理数减法法则:
减去一个数,等于加上这个数的相反数
谢谢观看
