黑龙江省大庆市肇州县(五四学制)2020-2021学年八年级下学期期末考试数学试题(word版 含答案)
文档属性
| 名称 | 黑龙江省大庆市肇州县(五四学制)2020-2021学年八年级下学期期末考试数学试题(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览


文档简介
肇州县2020-2021学年度第二学期期末检测
初三数学试卷
选择(每题3分共24分)
1.如图立体图形中,三视图都一样的是(
)
A
B
C
D
2.下列命题中,是真命题的是(
)
A.
两条对角线互相平分的四边形是平行四边形
B.
两条对角线相等的四边形是矩形
C.
两条对角线互相垂直的四边形是菱形
D.
两条对角线互相垂直且相等的四边形是正方形
3.从正方形的铁片上截去2
cm宽的长方形,余下的面积是48
cm2,则原来的正方形铁片的面积是(
)
A.
8
cm2
B.
32
cm2
C.
64
cm2
D.
96
cm2
4.
若关于x的方程x2+2x+a=0不存在实数根,则a的取值范围是( )
A.
a<1
B.
a>1
C.
a≤1
D.
a≥1
5.
从单词“happy”中随机抽取一个字母,抽中p的概率为( )
A.
B.
C.
D.
6.关于反比例函数的图象,下列说法正确的是(
)
A.点(-2,1)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
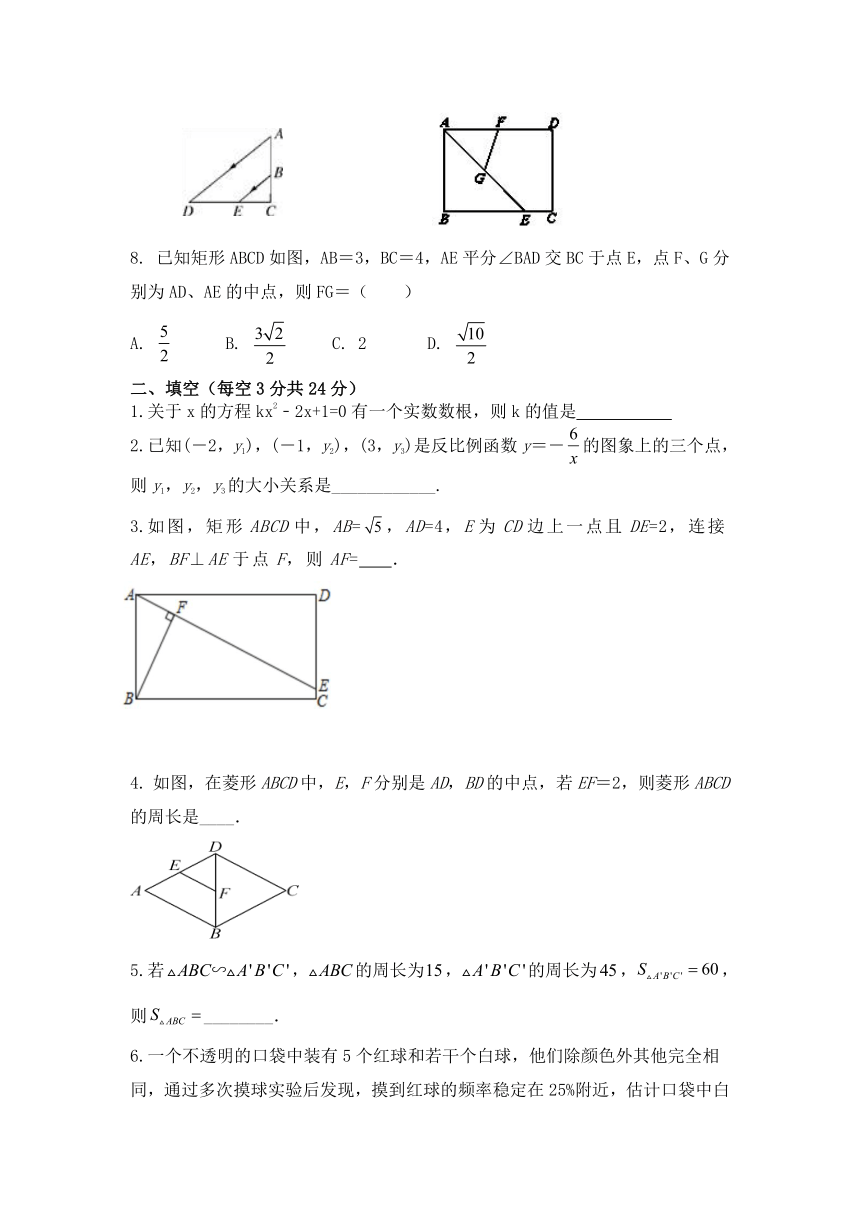
7.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为(
)
A.
1.5m
B.
1.6m
C.
1.86m
D.
2.16m
8.
已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=(
)
A.
B.
C.
2
D.
二、填空(每空3分共24分)
1.关于x的方程kx2﹣2x+1=0有一个实数数根,则k的值是
2.已知(-2,y1),(-1,y2),(3,y3)是反比例函数y=-的图象上的三个点,则y1,y2,y3的大小关系是____________.
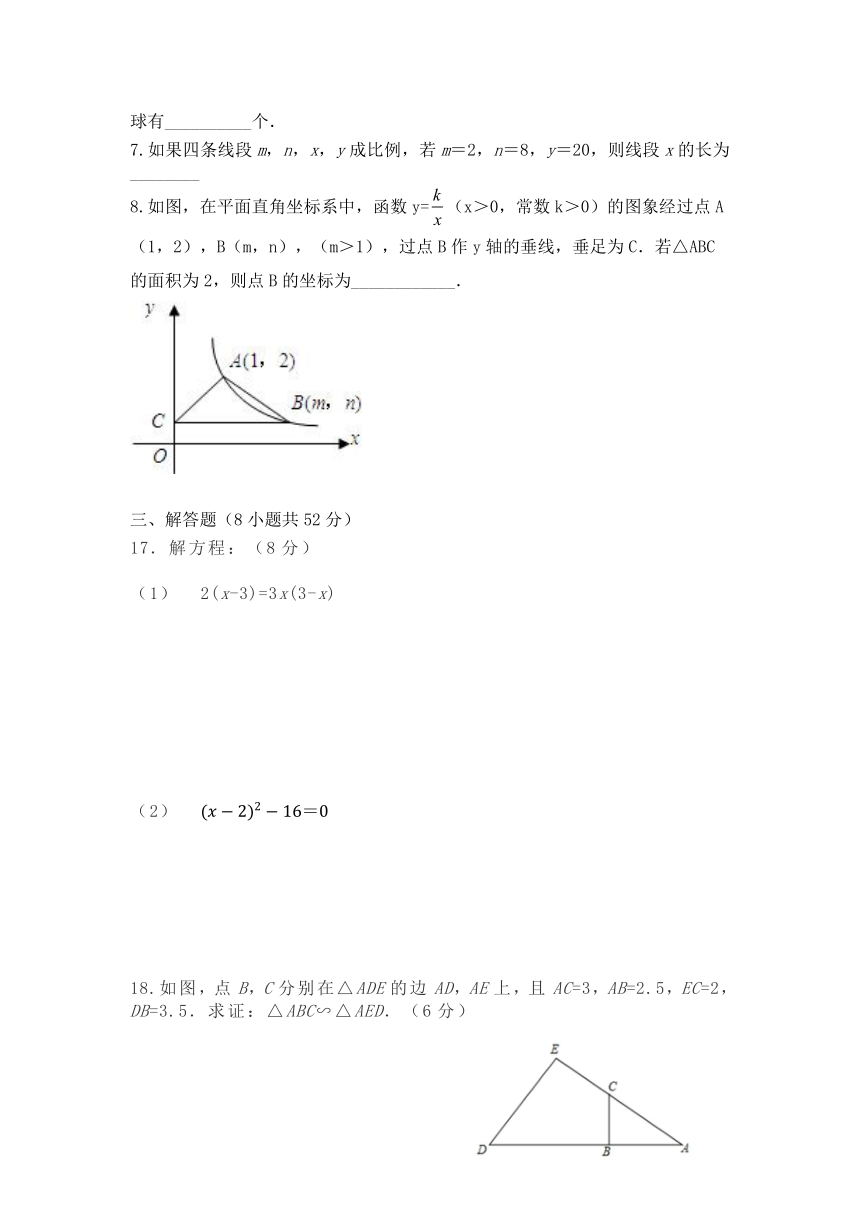
3.如图,矩形ABCD中,AB=,AD=4,E为CD边上一点且DE=2,连接AE,BF⊥AE于点F,则AF=
.
如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是____.
5.若,的周长为,的周长为,,则________.
6.一个不透明的口袋中装有5个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,估计口袋中白球有__________个.
7.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长为________
8.如图,在平面直角坐标系中,函数y=(x>0,常数k>0)的图象经过点A(1,2),B(m,n),(m>1),过点B作y轴的垂线,垂足为C.若△ABC的面积为2,则点B的坐标为____________.
三、解答题(8小题共52分)
17.解方程:(8分)
(1)
2(x-3)=3x(3-x)
(2)
=
18.如图,点B,C分别在△ADE的边AD,AE上,且AC=3,AB=2.5,EC=2,DB=3.5.求证:△ABC∽△AED.(6分)
某市体育局要组织一次蓝球赛,赛制为单循环形式(每两队之间都赛一场)计划安排28场比赛,问应邀请多少支球队参加比赛?(6分)
20.
已知关于的一元二次方程总有两个不相等的实数根.
(6分)
求的取值范围;
21.
已知:如图,在中,是的平分线,,.求证:四边形是菱形.(6分)
22.甲、乙、丙、丁四个人玩“击鼓传花”的游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.(6分)
(1)甲第一次传花时,恰好传给乙的概率是
;
(2)求经过两次传花后,花恰好回到甲手中的概率.
23.(7分)如图,一位同学想利用树影测量树(AB)的高度,他在某一时刻测得高为1米的竹竿直立时影长为0.9米,此时,因树靠近一幢建筑物,影子不全落在地面上(有一部分影子落在了墙上CD处),他先测得落在墙上的影子(CD)高为1.2米,又测得地面部分的影长(BC)为2.7米,则他测得的树高应为多少米?
24.(7分)如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=m/x的图象交于点B(﹣2,n),过B作BC⊥x轴于点C,D(3﹣3n,1)是反比例图象上一点,AB=5.
求:(1)反比例函数的表达式;
(2)求一次函数的表达式.
初三答案
CACBC
DAD
(1)0或1(2)y3<y1<y2(3)1(4)16(5)20/3(6)15(7)5(8)(3,2/3)
三、17.
解得:
x1=3,x2=-
解得:=,=
证明:∵AC=3,AB=2.5,EC=2,DB=3.5.
∴AE=5,AD=6.
∴,.
∴.
∵∠A=∠A,∴△ABC∽△AED.
8
20.解:由题意得:
且,
∴
当且时,原方程有两个不相等的实数根.
∵
此方程的两根均为正整数,即,
∴
,,∴
可取得的正整数的值分别为和,
又由知,,∴
.
21.解:∵
,,
∴
四边形是平行四边形,
∵
平分,
∴
(角平分线的定义),
∵
,∴
(两直线平行,内错角相等),
∴
(等量代换),∴
,
∴
平行四边形是菱形
22.解:(1).
(2)如图所示:
,
共有9种等可能的结果,其中符合要求的结果有3种故两次传花后,花恰好回到甲手中的概率为.
树高AB=AE+BE=3+1.2=4.2米.
24.(1)y=-6/x
(2)y=-3x/4+3/2
初三数学试卷
选择(每题3分共24分)
1.如图立体图形中,三视图都一样的是(
)
A
B
C
D
2.下列命题中,是真命题的是(
)
A.
两条对角线互相平分的四边形是平行四边形
B.
两条对角线相等的四边形是矩形
C.
两条对角线互相垂直的四边形是菱形
D.
两条对角线互相垂直且相等的四边形是正方形
3.从正方形的铁片上截去2
cm宽的长方形,余下的面积是48
cm2,则原来的正方形铁片的面积是(
)
A.
8
cm2
B.
32
cm2
C.
64
cm2
D.
96
cm2
4.
若关于x的方程x2+2x+a=0不存在实数根,则a的取值范围是( )
A.
a<1
B.
a>1
C.
a≤1
D.
a≥1
5.
从单词“happy”中随机抽取一个字母,抽中p的概率为( )
A.
B.
C.
D.
6.关于反比例函数的图象,下列说法正确的是(
)
A.点(-2,1)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
7.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为(
)
A.
1.5m
B.
1.6m
C.
1.86m
D.
2.16m
8.
已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=(
)
A.
B.
C.
2
D.
二、填空(每空3分共24分)
1.关于x的方程kx2﹣2x+1=0有一个实数数根,则k的值是
2.已知(-2,y1),(-1,y2),(3,y3)是反比例函数y=-的图象上的三个点,则y1,y2,y3的大小关系是____________.
3.如图,矩形ABCD中,AB=,AD=4,E为CD边上一点且DE=2,连接AE,BF⊥AE于点F,则AF=
.
如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是____.
5.若,的周长为,的周长为,,则________.
6.一个不透明的口袋中装有5个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,估计口袋中白球有__________个.
7.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长为________
8.如图,在平面直角坐标系中,函数y=(x>0,常数k>0)的图象经过点A(1,2),B(m,n),(m>1),过点B作y轴的垂线,垂足为C.若△ABC的面积为2,则点B的坐标为____________.
三、解答题(8小题共52分)
17.解方程:(8分)
(1)
2(x-3)=3x(3-x)
(2)
=
18.如图,点B,C分别在△ADE的边AD,AE上,且AC=3,AB=2.5,EC=2,DB=3.5.求证:△ABC∽△AED.(6分)
某市体育局要组织一次蓝球赛,赛制为单循环形式(每两队之间都赛一场)计划安排28场比赛,问应邀请多少支球队参加比赛?(6分)
20.
已知关于的一元二次方程总有两个不相等的实数根.
(6分)
求的取值范围;
21.
已知:如图,在中,是的平分线,,.求证:四边形是菱形.(6分)
22.甲、乙、丙、丁四个人玩“击鼓传花”的游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.(6分)
(1)甲第一次传花时,恰好传给乙的概率是
;
(2)求经过两次传花后,花恰好回到甲手中的概率.
23.(7分)如图,一位同学想利用树影测量树(AB)的高度,他在某一时刻测得高为1米的竹竿直立时影长为0.9米,此时,因树靠近一幢建筑物,影子不全落在地面上(有一部分影子落在了墙上CD处),他先测得落在墙上的影子(CD)高为1.2米,又测得地面部分的影长(BC)为2.7米,则他测得的树高应为多少米?
24.(7分)如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=m/x的图象交于点B(﹣2,n),过B作BC⊥x轴于点C,D(3﹣3n,1)是反比例图象上一点,AB=5.
求:(1)反比例函数的表达式;
(2)求一次函数的表达式.
初三答案
CACBC
DAD
(1)0或1(2)y3<y1<y2(3)1(4)16(5)20/3(6)15(7)5(8)(3,2/3)
三、17.
解得:
x1=3,x2=-
解得:=,=
证明:∵AC=3,AB=2.5,EC=2,DB=3.5.
∴AE=5,AD=6.
∴,.
∴.
∵∠A=∠A,∴△ABC∽△AED.
8
20.解:由题意得:
且,
∴
当且时,原方程有两个不相等的实数根.
∵
此方程的两根均为正整数,即,
∴
,,∴
可取得的正整数的值分别为和,
又由知,,∴
.
21.解:∵
,,
∴
四边形是平行四边形,
∵
平分,
∴
(角平分线的定义),
∵
,∴
(两直线平行,内错角相等),
∴
(等量代换),∴
,
∴
平行四边形是菱形
22.解:(1).
(2)如图所示:
,
共有9种等可能的结果,其中符合要求的结果有3种故两次传花后,花恰好回到甲手中的概率为.
树高AB=AE+BE=3+1.2=4.2米.
24.(1)y=-6/x
(2)y=-3x/4+3/2
同课章节目录
