平行四边形的性质

(共27张PPT)
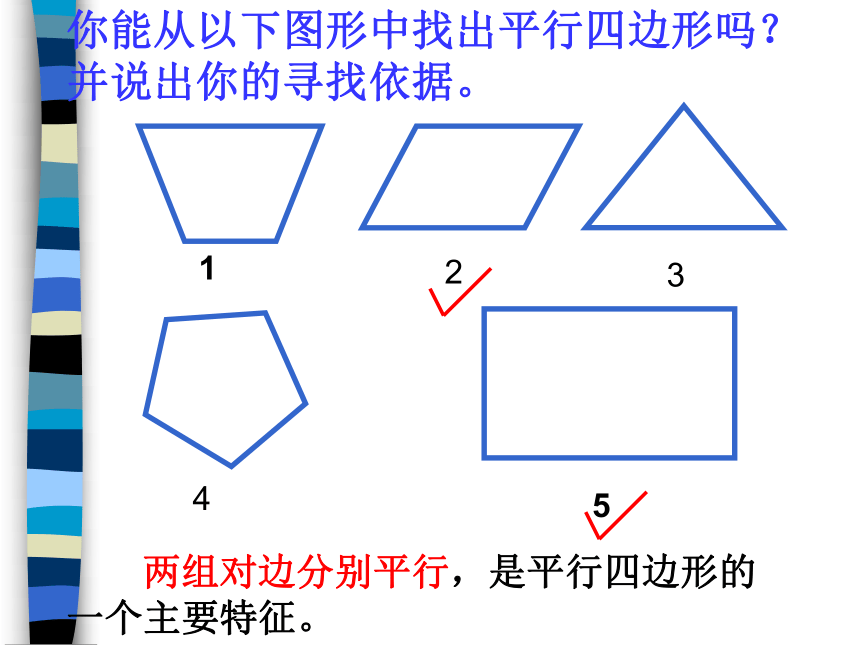
你能从以下图形中找出平行四边形吗？并说出你的寻找依据。
两组对边分别平行，是平行四边形的一个主要特征。
2
3
1
4
5
对边 邻边 对角 邻角
对角线．
如图:线段AC、BD就是 ABCD的对角线
A
D
C
B
1.两组对边分别平行的四边形叫做平行四边形.
如图：四边形ABCD是平行四边形
记作： ABCD
读作：平行四边形ABCD
请同学们指出图中的
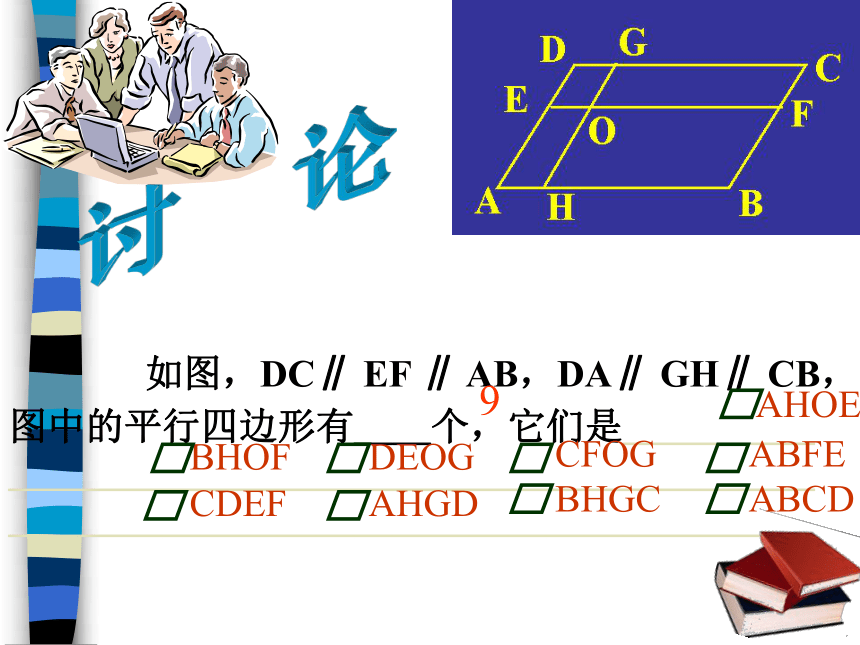
如图，DC∥ EF ∥ AB，DA∥ GH∥ CB，图中的平行四边形有＿＿个，它们是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
A
B
D
C
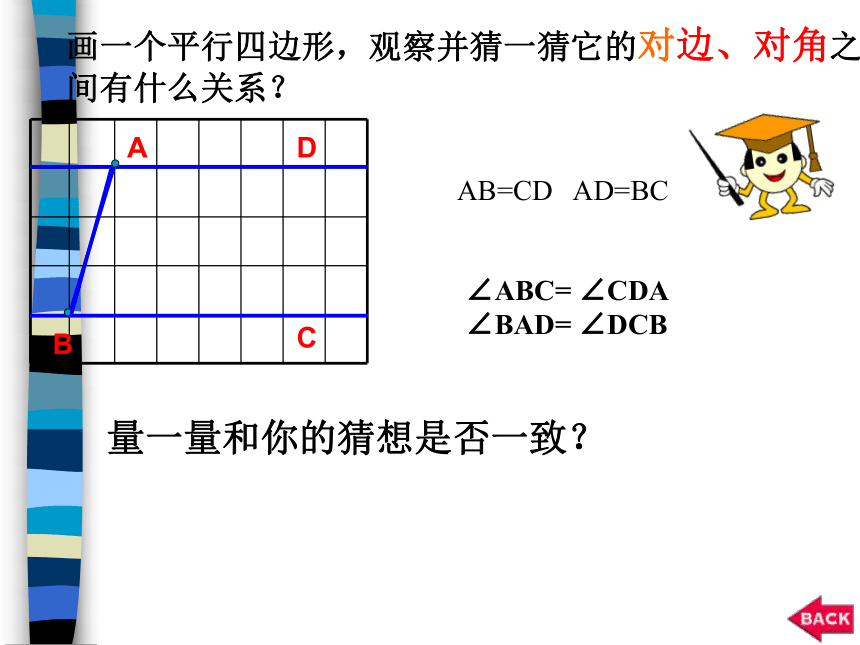
画一个平行四边形，观察并猜一猜它的对边、对角之间有什么关系？
量一量和你的猜想是否一致？
AB=CD AD=BC
∠ABC= ∠CDA
∠BAD= ∠DCB
操作、观察、猜想、合作探究、归纳
请同学们按下面要求操作：
（1）请同学们把刚才画的平行四边形，记作　　　　　　　　　　　　　　　　　　　　　　　　　　ＡＢＣＤ，连接对角线AC，ＢＤ相交于点O
（２）用准备好的透明纸印着刚才画的 ABCD画一个同样的图形
（3）用图钉订住对角线的交点，把其中一个旋转180度
请同学们说出看到的现象，并根据你看到的现象.
进一步验证猜想
探究
旋转平行四边形，探究其边、角的关系
C
A
B
D
O
A
B
C
D
结论 1 ： AB=CD，AD=BC
结论2：
平行四边形的对边相等
平行四边形的对角相等
已知： ABCD（如图）
求证：AB=CD，BC=DA；∠B=∠D，∠BAD=∠DCB
即∠BAD＝∠DCB
证明：连结AC
∵AB∥CD，AD∥BC（平行四边形的对边平行）
∴∠1＝∠2，∠3＝∠4
∠1＝∠2，AC＝CA，∠3＝∠4
∴ ABC≌ CDA（ASA）
∴AB＝CD，BC＝DA，∠B＝∠D
又∵∠1＝∠2，∠3＝∠4
∴∠1＋∠4＝∠2＋∠3
在 ABC和 CDA中
A
B
C
D
1
2
3
4
完善：
性质1、平行四边形的对边平行且相等。
性质2、平行四边形的对角相等，邻角互补
。
推理：
AB=CD，AD=BC ，AB ∥CD AD ∥BC
边：
角：
归纳：
操作：
平行四边形的性质：
A
B
C
D
1．填空题：
（1）在 ABCD中， ， ， ，那么 ABCD的周长为 ______， _______， _______， ________。

2.在 ABCD 中，∠ADC=120°， ∠CAD=20°，则∠ABC= ， ∠CAB=
（3）如图，已知点C在BD上，△ABC中
,且四边形ACDE是平行四边形，
那么，图中与ED相等的线段有_________；
与 相等的角有 。
2、如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F.
求证：∠BAE＝∠DCF。
A
B
C
D
E
F
A
B
C
D
E
3、如图：在笔直的铁轨上夹在两根铁轨之间的枕
木是否一样长？
平行四边形的对边平行且相等；
B
D
C
A
平行四边形的对角相等；邻角互补。
有两组对边分别平行的四边形是平行四边形。
数学方法：证明平行、线段相等、角相等的新方法。
数学思想：将平行四边形转化为三角形的过程。
作业布置:
1、阅读本节内容， 把你所学的知识总结在笔记本上
2、书面作业：P84练习题第1、2题；
P90 第1题；P91第6题