黑龙江省大庆市肇州县(五四学制)2020-2021学年七年级下学期期末考试数学试题(word版 含答案)
文档属性
| 名称 | 黑龙江省大庆市肇州县(五四学制)2020-2021学年七年级下学期期末考试数学试题(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 17:53:01 | ||
图片预览




文档简介
肇州县2020-2021学年度第二学期期末检测
初二数学试卷
一、选择(共8小题每题3分)
1.
下列说法正确的是(
)
A.
若a、b、c是△ABC的三边,则a2b2c2;
B.
若a、b、c是Rt△ABC的三边,则a2b2c2;
C.
若a、b、c是Rt△ABC三边,∠A=90°,则a2b2c2;
D.
若a、b、c是Rt△ABC的三边,∠C=90°,则a2b2c2.
2.已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
A.
B.
C.
D.
3.下列二次根式中,与是同类二次根式的是( )
A.
B.
C.
D.
4.若以B点为原点,建立平面直角坐标系,A点坐标为(3,4),则以A点为原点,建立平面直角坐标系,B点坐标为(
)
A.(-3,-4)
B.(-3,4)
C.(3,-4)
D.(3,4)
5.已知是方程2x﹣ay=3的一个解,那么a的值是( )
A.
-3
B.
3
C.
1
D.
﹣1
6.
一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数,中位数分别为( )
A.
3.5,3
B.
3,4
C.
3,3.5
D.
4,3
7.如图,AB∥CD,∠C=110°,∠B=120°,则∠BEC等于
( )
A.
110°
B.
120°
C.
130°
D.
150°
8.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4
B.5
C.6
D.7
二、填空(共8小题每题3分)
9.若三角形三个内角度数的比为3:4:5,则此三角形是
______
三角形(填锐角、直角或钝角)。
10.在函数y=-3x+5的图象上有A(1,y1),B(-1,y2),C(-2,y3)三个点,则y1,y2,y3的大小关系是_____________。
11.若的整数部分是a小数部分是b,则a-b等于__________。
12.64的算术平方根为______
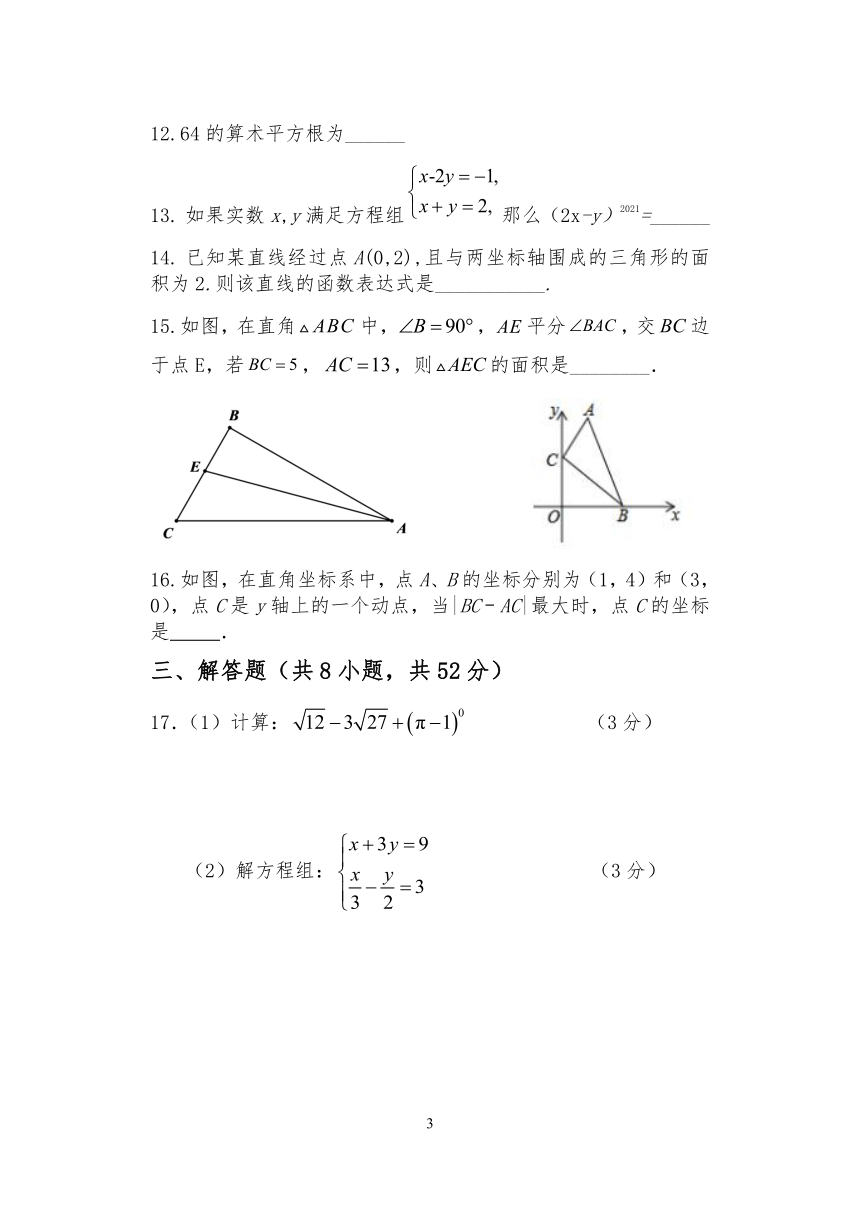
如果实数x,y满足方程组那么(2x-y)2021=______
已知某直线经过点A(0,2),且与两坐标轴围成的三角形的面积为2.则该直线的函数表达式是___________.
15.如图,在直角中,,平分,交边于点E,若,,则的面积是________.
16.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,当|BC﹣AC|最大时,点C的坐标是
.
三、解答题(共8小题,共52分)
17.(1)计算:
(3分)
(2)解方程组:
(3分)
18.如图,,平分交于点.若,求的度数.(6分)
19.(6分)如图,铁路上、两点相距,,为两村庄,于,于,已知,,现在要在铁路上建一个土特产品收购站,使得、两村到站的距离相等,则站应建在距点多少千米处?
20.(6分)在若干所中学联合举办的田径运动会上,各位运动员成绩优异,表现突出.为了了解参加跳高比赛的男子组选手的整体水平,现抽取一部分选手的跳高成绩(单位:)进行统计分析,并绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)图①中的值为______;
(2)求统计的这组跳高成绩中众数、平均数和中位数;
(3)若本次参加男子跳高比赛的选手有300名,请你估算本次跳高比赛中成绩在及以上的选手有多少名?
21.(6分)在2021年双11到来之前,某商家为了囤货,投入28000元资金购进、两种商品共1000件,两种商品的成本价和销售价如下表所示:
商品
单价(元/件)
成本价
销售价
25
35
30
45
(1)该商家购进两种商品各多少件?
(2)这批商品全部销售完后,该商家共获利多少元?
22.(7分)某市为了鼓励全民节约用水,制定了新的两级收费制度.按照新标准,用户每月缴纳的水费(元)与每月用水量之间的关系如图所示.
(1)求关于的函数解析式;
(2)若某用户三月份缴纳水费63元,则该用户三月份的用水量是多少?
23.(7分)如图,直线与轴交于点,直线经过点、,点的坐标为,且两直线相交于点.
(1)求点的坐标;
(2)求的面积.
24.(8分)探究:如图①,,平分,平分,且点、、均在直线上,直线分别与、交于点、.
(1)若,,则______.
(2)若,求的度数.
(3)如图②,和的平分线、交于点,经过点且平行于,分别与、交于点、.若,直接写出的度数.
(用含的代数式表示)
初二答案
DABAC
ACB
二、9、锐角
10、y1<y2<y3
11、1
12、8
13、1
14、y=x+2或y=-x+2
15、78/5
16、(0,6)
三、17(1)解:原式
(2)∴该二元一次方程组的解为
18、证明:∵,∴,
∵平分,∴,
又∵,∴.
19、解:设,则,
∵、两村到站的距离相等,∴.
在中,由勾股定理得,
在中,由勾股定理得,
∴,
又∵,,∴,∴,
站应建在距点10千米处.
20、解:(1)25.
(2)众数为1.65m;中位数为1.60m,
平均数m.
(3)(名).
答:本次跳高比赛中成绩在及以上的选手有210名.
21解:(1)设购进种商品件,购进种商品件
根据题意,得,解得.
∴该商家购进种商品400件,种商品600件.
(2).
∴该商家共获利13000元.
22.解:(1)当时,设,则,
∴,∴;当时,设,
∴,解得,
∴与的关系式是;
∵,∴该用户三月份的用水量超过15吨,当时,,∴,∴该用户三月份的用水量是
23.解:(1)设直线的解析式为
∵直线过,,
∴,解得,∴直线的解析式为,
联立方程得,解得,∴点的坐标是.
(2)∵直线与轴交于点,
∴令,得,解得:,
∴,∴,
∴
24(1)120°;
(2)∵平分,平分,
∴,.
∵,
∴.
∵,
∴.
(3)∵平分,平分,
∴,,
∴
.
初二数学试卷
一、选择(共8小题每题3分)
1.
下列说法正确的是(
)
A.
若a、b、c是△ABC的三边,则a2b2c2;
B.
若a、b、c是Rt△ABC的三边,则a2b2c2;
C.
若a、b、c是Rt△ABC三边,∠A=90°,则a2b2c2;
D.
若a、b、c是Rt△ABC的三边,∠C=90°,则a2b2c2.
2.已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
A.
B.
C.
D.
3.下列二次根式中,与是同类二次根式的是( )
A.
B.
C.
D.
4.若以B点为原点,建立平面直角坐标系,A点坐标为(3,4),则以A点为原点,建立平面直角坐标系,B点坐标为(
)
A.(-3,-4)
B.(-3,4)
C.(3,-4)
D.(3,4)
5.已知是方程2x﹣ay=3的一个解,那么a的值是( )
A.
-3
B.
3
C.
1
D.
﹣1
6.
一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数,中位数分别为( )
A.
3.5,3
B.
3,4
C.
3,3.5
D.
4,3
7.如图,AB∥CD,∠C=110°,∠B=120°,则∠BEC等于
( )
A.
110°
B.
120°
C.
130°
D.
150°
8.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4
B.5
C.6
D.7
二、填空(共8小题每题3分)
9.若三角形三个内角度数的比为3:4:5,则此三角形是
______
三角形(填锐角、直角或钝角)。
10.在函数y=-3x+5的图象上有A(1,y1),B(-1,y2),C(-2,y3)三个点,则y1,y2,y3的大小关系是_____________。
11.若的整数部分是a小数部分是b,则a-b等于__________。
12.64的算术平方根为______
如果实数x,y满足方程组那么(2x-y)2021=______
已知某直线经过点A(0,2),且与两坐标轴围成的三角形的面积为2.则该直线的函数表达式是___________.
15.如图,在直角中,,平分,交边于点E,若,,则的面积是________.
16.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,当|BC﹣AC|最大时,点C的坐标是
.
三、解答题(共8小题,共52分)
17.(1)计算:
(3分)
(2)解方程组:
(3分)
18.如图,,平分交于点.若,求的度数.(6分)
19.(6分)如图,铁路上、两点相距,,为两村庄,于,于,已知,,现在要在铁路上建一个土特产品收购站,使得、两村到站的距离相等,则站应建在距点多少千米处?
20.(6分)在若干所中学联合举办的田径运动会上,各位运动员成绩优异,表现突出.为了了解参加跳高比赛的男子组选手的整体水平,现抽取一部分选手的跳高成绩(单位:)进行统计分析,并绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)图①中的值为______;
(2)求统计的这组跳高成绩中众数、平均数和中位数;
(3)若本次参加男子跳高比赛的选手有300名,请你估算本次跳高比赛中成绩在及以上的选手有多少名?
21.(6分)在2021年双11到来之前,某商家为了囤货,投入28000元资金购进、两种商品共1000件,两种商品的成本价和销售价如下表所示:
商品
单价(元/件)
成本价
销售价
25
35
30
45
(1)该商家购进两种商品各多少件?
(2)这批商品全部销售完后,该商家共获利多少元?
22.(7分)某市为了鼓励全民节约用水,制定了新的两级收费制度.按照新标准,用户每月缴纳的水费(元)与每月用水量之间的关系如图所示.
(1)求关于的函数解析式;
(2)若某用户三月份缴纳水费63元,则该用户三月份的用水量是多少?
23.(7分)如图,直线与轴交于点,直线经过点、,点的坐标为,且两直线相交于点.
(1)求点的坐标;
(2)求的面积.
24.(8分)探究:如图①,,平分,平分,且点、、均在直线上,直线分别与、交于点、.
(1)若,,则______.
(2)若,求的度数.
(3)如图②,和的平分线、交于点,经过点且平行于,分别与、交于点、.若,直接写出的度数.
(用含的代数式表示)
初二答案
DABAC
ACB
二、9、锐角
10、y1<y2<y3
11、1
12、8
13、1
14、y=x+2或y=-x+2
15、78/5
16、(0,6)
三、17(1)解:原式
(2)∴该二元一次方程组的解为
18、证明:∵,∴,
∵平分,∴,
又∵,∴.
19、解:设,则,
∵、两村到站的距离相等,∴.
在中,由勾股定理得,
在中,由勾股定理得,
∴,
又∵,,∴,∴,
站应建在距点10千米处.
20、解:(1)25.
(2)众数为1.65m;中位数为1.60m,
平均数m.
(3)(名).
答:本次跳高比赛中成绩在及以上的选手有210名.
21解:(1)设购进种商品件,购进种商品件
根据题意,得,解得.
∴该商家购进种商品400件,种商品600件.
(2).
∴该商家共获利13000元.
22.解:(1)当时,设,则,
∴,∴;当时,设,
∴,解得,
∴与的关系式是;
∵,∴该用户三月份的用水量超过15吨,当时,,∴,∴该用户三月份的用水量是
23.解:(1)设直线的解析式为
∵直线过,,
∴,解得,∴直线的解析式为,
联立方程得,解得,∴点的坐标是.
(2)∵直线与轴交于点,
∴令,得,解得:,
∴,∴,
∴
24(1)120°;
(2)∵平分,平分,
∴,.
∵,
∴.
∵,
∴.
(3)∵平分,平分,
∴,,
∴
.
同课章节目录
