沪科版八年级上册数学 第14章全等三角形 判定方法专题训练(word版含答案)
文档属性
| 名称 | 沪科版八年级上册数学 第14章全等三角形 判定方法专题训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 296.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览




文档简介
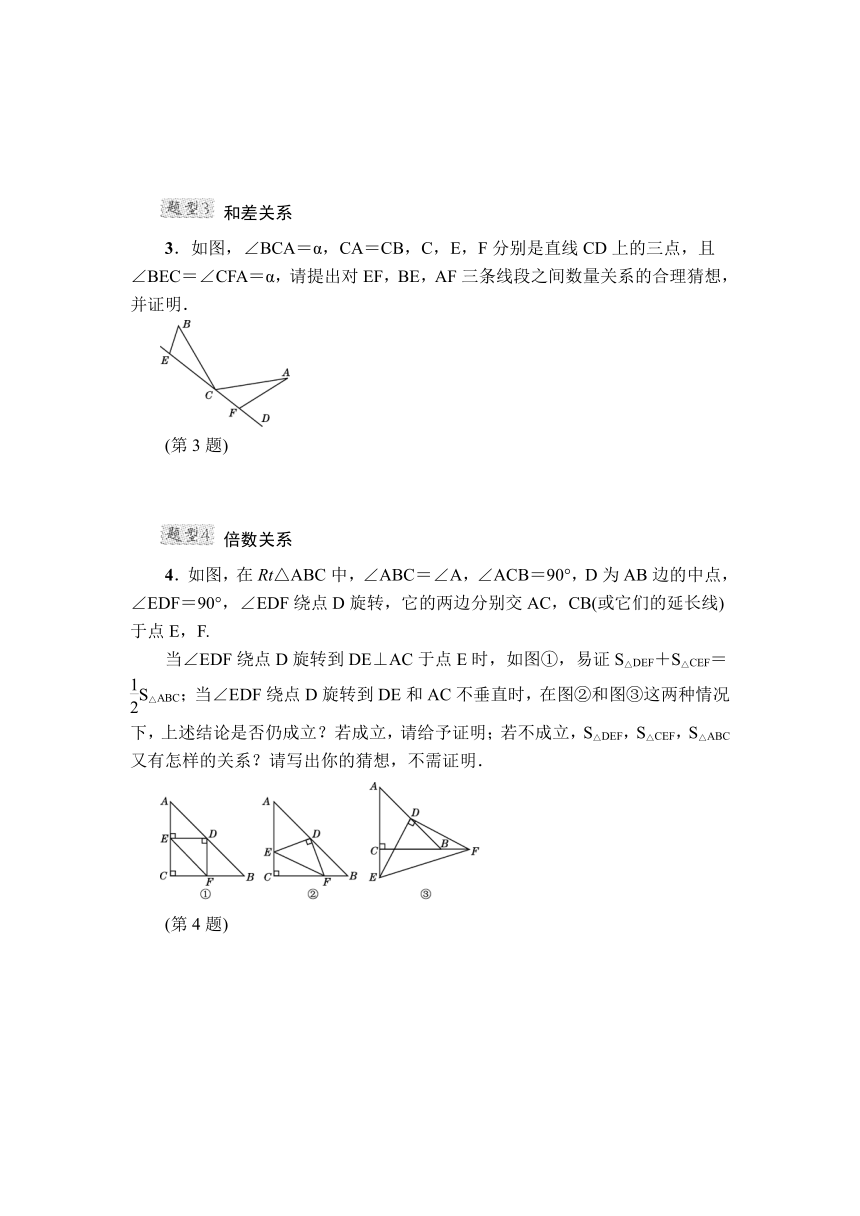
专训一:四种常见的几何关系的探究
名师点金:全等三角形的性质和判定是初中数学的重点内容,也是学习其他几何知识的基础,三角形全等的判定和性质是证明线段相等、角相等的重要依据,并由此还可以获得直线之间的垂直(平行)关系,线段(面积)的和、差、倍、分关系.
位置关系
1.如图,已知BE⊥AC,CF⊥AB,BM=AC,CN=AB.求证:AM⊥AN.
(第1题)
相等关系
2.(2015·珠海)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.
(1)如图①,连接BD,AF,则BD________AF.(填“>”,“<”或“=”号)
(2)如图②,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF.求证:BH=GF.
(第2题)
和差关系
3.如图,∠BCA=α,CA=CB,C,E,F分别是直线CD上的三点,且∠BEC=∠CFA=α,请提出对EF,BE,AF三条线段之间数量关系的合理猜想,并证明.
(第3题)
倍数关系
4.如图,在Rt△ABC中,∠ABC=∠A,∠ACB=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.
当∠EDF绕点D旋转到DE⊥AC于点E时,如图①,易证S△DEF+S△CEF=S△ABC;当∠EDF绕点D旋转到DE和AC不垂直时,在图②和图③这两种情况下,上述结论是否仍成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?请写出你的猜想,不需证明.
(第4题)
专训二:构造全等三角形的六种常用方法
名师点金:在进行几何题的证明或计算时,需要在图形中添加一些辅助线,辅助线能使题目中的条件比较集中,能比较容易找到一些量之间的关系,使数学问题较轻松地解决.常见的辅助线作法有:构造法、平行线法、旋转法、翻折法、倍长中线法和截长补短法,目的都是构造全等三角形.
翻折法
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.
(第1题)
构造法
2.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.
求证:∠ADC=∠BDF.
(第2题)
旋转法
3.如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
(第3题)
平行线法
4.在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC交AC于点Q,且AP与BQ相交于点O.求证:AB+BP=BQ+AQ.
(第4题)
倍长中线法
5.如图,在△ABC中,D为BC的中点.
(1)求证:AB+AC>2AD;
(2)若AB=5,AC=3,求AD的取值范围.
(第5题)
截长补短法
6.如图,AB∥CD,CE,BE分别平分∠BCD和∠CBA,点E在AD上.求证:BC=AB+CD.
(第6题)
专训三:全等三角形的四种常见实际应用
名师点金:利用三角形全等解决实际问题的步骤:
(1)明确应用哪些知识来解决实际问题;(2)根据实际问题抽象出几何图形;
(3)结合图形和题意分析已知条件;(4)找到已知与未知的联系,寻求恰当的解决途径,并表述清楚.
利用三角形全等测量池塘两端的距离
1.如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
(第1题)
利用三角形全等测量物体的内径
2.如图,已知零件的外径为a,要求它的厚度x,动手制作一个简单的工具,利用三角形全等的知识,求出x.
(第2题)
利用三角形全等判断三点是否共线
3.如图,公园里有一条“Z”形道路ABCD,其中AB∥CD,在AB,BC,CD三段路路旁各有一个石凳E,M,F,且BE=CF,石凳M在BC的中点处,试判断三个石凳E,M,F是否恰好在一条直线上?为什么?
(第3题)
利用三角形全等解决工程中的问题
4.如图,工人师傅要在墙壁的点O处用钻打孔,要使孔口从墙壁对面的点B处打开,墙壁厚35 cm,点B与点O的垂直距离AB长20 cm,在点O处作一直线平行于地面,再在直线上截取OC=35 cm,过点C作OC的垂线,在垂线上截取CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从点B处打出,这是什么道理?
(第4题)
专训四:几类常见的热门考点
名师点金:本章主要学习了全等三角形的性质与判定,其考查形式有利用全等三角形证明线段或角的数量关系,求线段的长度或角的度数,判断位置关系,以及利用全等三角形解决实际问题等.
全等三角形的性质
1.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式中不正确的是( )
(第1题)
A.AB=AC
B.∠BAE=∠CAD
C.BD=CE
D.AD=DE
2.已知△ABC≌△A′B′C′,∠A=∠A′=50°,∠B=∠B′=60°,AB=15 cm,则∠C′的度数为________,A′B′的长度为________.
3.如图,已知△ABC≌△ADE,BC边的延长线交AD于点F,交AE的延长线于点G,∠ACB=105°,∠CAD=15°,∠ADE=25°,求∠DFB和∠G的度数.
(第3题)
全等三角形的判定
4.在△ABC和△A′B′C′中,下列各组条件中,不能判定△ABC≌△A′B′C′的是( )
①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′.
A.具备①②③ B.具备①②④
C.具备③④⑤ D.具备②③⑥
(第5题)
5.如图,已知BC=EC,∠A=∠D,要使△ABC≌△DEC,则应添加的一个条件为________(只需填一个).
6.(中考·宁德)如图所示,点D,A,C在同一直线上,AB∥CE,AB=CD,∠B=∠D.
求证:△ABC≌△CDE.
(第6题)
全等三角形的性质与判定的综合应用
7.如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的是( )
(第7题)
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠DAE=40°
D.∠C=30°
8.(2014·黄冈)如图所示,AB=AC,BD=CD,DE⊥AB交AB的延长线于点E,DF⊥AC交AC的延长线于点F.求证:DE=DF.
(第8题)
9.如图,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(第9题)
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
全等三角形在实际问题中的应用
10.某校七(3)班学生到野外活动,为测量一池塘两端A,B之间的距离,设计了如下方案:
方案一:如图①,先在平地上取一个可以直接到达A,B的点C,连接AC,BC,并延长AC到点D,延长BC到点E,使DC=AC,EC=BC,最后测出DE的长即为A,B之间的距离.
(第10题)
方案二:如图②,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,测出DE的长即为A,B之间的距离.
阅读后回答下列问题:
(1)方案一是否切实可行?________,理由是________________________________________________________________________
________________________________________________________________________.
(2)方案二是否切实可行?________,理由是________________________________________________________________________
________________________________________________________________________.
(3)方案二中作BF⊥AB,ED⊥BF的目的是__________________________;若∠ABD=∠BDE,但不一定垂直,方案二是否成立?__________________.
数学思想方法的应用
a.转化思想
11.如图,AB=DC,∠A=∠D.求证:∠ABC=∠DCB.
(第11题)
b.分类讨论思想
12.如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点.点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
(第12题)
c.类比思想
13.在△ABC中,若AD是∠BAC的平分线,E点和F点分别在AB和AC上,且DE⊥AB,垂足为E,DF⊥AC,垂足为F,如图①,则可以得到以下两个结论:①∠AED+∠AFD=180°;②DE=DF.那么在△ABC中,仍然有条件“AD是∠BAC的平分线,点E和点F分别在AB和AC上”,请探究以下两个问题:
(1)若∠AED+∠AFD=180°,如图②,则DE与DF是否仍相等?若仍相等,请证明;否则请说明理由.
(2)若DE=DF,则∠AED+∠AFD=180°是否成立?(只写出结论,不证明)
(第13题)
答案
专训一
1.证明:如图,∵BE⊥AC,CF⊥AB,∴∠1+∠BAC=90°,∠2+∠BAC=90°.∴∠1=∠2.又∵BM=CA,AB=NC,∴△ABM≌△NCA.∴∠3=∠N.
∵∠N+∠4=90°,∴∠3+∠4=90°,即∠MAN=90°.∴AM⊥AN.
(第1题)
(第2题)
2.(1)=
(2)证明:将△DEF沿FE方向平移,使点E与点C重合,设ED平移后与MN相交于R,如图,
∵MN∥BC,RC∥EH,
∴∠GRC=∠RHE=∠DEF,∠RGC=∠GCB,
易得∠GRC=∠RGC,过点C作CZ⊥GR,∴∠CZR=∠CZG=90°,
又∵CZ=CZ,∴△CZR≌△CZG,
∴CR=CG.
又∵MN∥BF,CR∥EH,∴四边形RCEH为平行四边形,∴CR=EH.∴CG=HE.
由平移的性质得BC=EF,
∴BC+CE=CE+EF,即BE=CF.
易得∠HEB=∠GCF,∴△BEH≌△FCG(SAS),
∴BH=FG.
3.解:猜想:EF=BE+AF.
证明:∵∠BCE+∠CBE+∠BEC=180°,
∠BCE+∠ACF+∠BCA=180°,
∠BCA=α=∠BEC,
∴∠CBE=∠ACF.
又∵∠BEC=∠CFA=α,CB=AC,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.∴EF=CF+EC=BE+AF.
(第4题)
4.解:在题图(2)中结论仍成立;在题图(3)中不成立.
对于题图(2)证明如下:
如图,过点D作DM⊥AC,DN⊥BC,垂足分别为M,N,
则∠DME=∠DNF=∠MDN=90°.
又∵∠A=∠ABC,∠AMD=∠BND=90°,
且易知DA=DB,
∴△ADM≌△BDN,∴DM=DN.
∵∠MDE+∠EDN=∠MDN=90°,∠EDN+∠NDF=∠EDF=90°,
∴∠MDE=∠NDF.
∴△DME≌△DNF.
∴S四边形DMCN=S四边形DECF=S△DEF+S△CEF.由题图(1)可知S四边形DMCN=S△ABC,∴S△DEF+S△CEF=S△ABC.
在题图(3)中,S△DEF,S△CEF,S△ABC之间的关系是S△DEF-S△CEF=S△ABC.
专训二
1.证明:如图,延长AD交BC于点F.(相当于将AB边向下翻折,与BC边重合,A点落在F点处,折痕为BE)
∵BE平分∠ABC,∴∠ABE=∠CBE.
∵BD⊥AD,∴∠ADB=∠BDF=90°.
在△ABD和△FBD中,
∴△ABD≌△FBD(ASA).
∴∠2=∠DFB.
又∵∠DFB=∠1+∠C,∴∠2=∠1+∠C.
(第1题)
(第2题)
2.证明:如图,过点B作BG⊥BC交CF的延长线于点G.
∵∠ACB=90°,∴∠2+∠ACF=90°.
∵CE⊥AD,∴∠AEC=90°,∴∠1+∠ACF=180°-∠AEC=180°-90°=90°.∴∠1=∠2.
在△ACD和△CBG中,
∴△ACD≌△CBG(ASA).
∴∠ADC=∠G,CD=BG.
∵点D为BC的中点,∴CD=BD.∴BD=BG.
又∵∠DBG=90°,∠DBF=45°,∴∠GBF=∠DBG-∠DBF=90°-45°=45°.∴∠DBF=∠GBF.
在△BDF和△BGF中,
∴△BDF≌△BGF(SAS).
∴∠BDF=∠G.∴∠ADC=∠BDF.
点拨:本题运用了构造法,通过作辅助线构造△CBG、△BGF是解题的关键.
3.解:如图,延长CB到点H,使得BH=DF,连接AH.
∵∠ABE=90°,∠D=90°,∴∠D=∠ABH=90°.
在△ABH和△ADF中,
∴△ABH≌△ADF.∴AH=AF,∠BAH=∠DAF.
∴∠BAH+∠BAF=∠DAF+∠BAF,即∠HAF=∠BAD=90°.
∵BE+DF=EF,∴BE+BH=EF,即HE=EF.
在△AEH和△AEF中,
(第3题)
∴△AEH≌△AEF.
∴∠EAH=∠EAF.
∴∠EAF=∠HAF=45°.
点拨:图中所作辅助线,相当于将△ADF绕点A顺时针旋转90°,使AD边与AB边重合,得到△ABH.
4.证明:过点O作OD∥BC交AB于点D,
∴∠ADO=∠ABC.∵∠BAC=60°,∠C=40°,
∴∠ABC=80°.∴∠ADO=80°.
∵BQ平分∠ABC,∴∠QBC=40°.∴∠AQB=∠C+∠QBC=80°.∴∠ADO=∠AQB.
易知∠DAO=∠QAO,OA=OA,∴△ADO≌△AQO.
∴OD=OQ,AD=AQ.
又∵OD∥BP,∴∠PBO=∠DOB.
又∵∠PBO=∠DBO,∴∠DBO=∠DOB.
∴过点D作DM⊥BQ,∴∠DMB=∠DMO=90°.
又∵DM=DM,∴△DMB≌△DMO.
∴BD=OD.∴BD=OQ.
∵∠BAC=60°,∠ABC=80°,BQ平分∠ABC,AP平分∠BAC,∴∠BAP=30°,∠ABQ=40°,∴∠BOP=70°.
∵∠BAP=30°,∠ABC=80°,∴∠APB=70°.
∴∠BOP=∠APB,过点B作BN⊥OP,
∴∠BNO=∠BNP=90°,
又∵BN=BN,∴△BNO≌△BNP.
∴BO=BP.∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ.
5.(1)证明:延长AD至点E,使DE=AD,连接BE.
∵D为BC的中点,∴CD=BD.
又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.
∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
(2)解:∵AB-BE∴AB-AC<2AD∵AB=5,AC=3,∴2<2AD<8.∴1点拨:本题运用了倍长中线法构造全等三角形,将证明不等关系和求线段取值范围的问题转化为证全等,从而利用全等三角形的性质解决问题.
6.证明:方法一:如图①,在BC上取一点F,使BF=BA.连接EF.∵CE,BE分别平分∠BCD和∠CBA,∴∠3=∠4,∠1=∠2.
在△ABE和△FBE中,
∴△ABE≌△FBE(SAS).∴∠A=∠5.
∵AB∥CD,∴∠A+∠D=180°.
而∠5+∠6=180°,∴∠6=∠D.
在△EFC和△EDC中,
∴△EFC≌△EDC(AAS),
∴FC=DC.∴BC=BF+CF=AB+CD.
(第6题)
方法二:如图②,分别延长BA,CE交于点F.
∵AB∥CD,∴∠ABC+∠BCD=180°.
∵CE,BE分别平分∠BCD和∠CBA,
∴∠1=∠2=∠ABC,∠3=∠4=∠BCD.
∴∠2+∠3=(∠ABC+∠BCD)=90°.
∴∠BEC=90°.∴∠BEF=∠BEC=90°.
在△BEC和△BEF中,
∴△BEC≌△BEF(ASA).∴BC=BF,EC=EF.
∵AB∥CD,∴∠7=∠D,∠F=∠4.
在△EAF和△EDC中,
∴△EAF≌△EDC(AAS).∴FA=CD.
∴BC=BF=BA+AF=AB+CD.
点拨:本题运用了两种不同的方法解题,方法一是截长法,方法二是补短法,这两种方法都是证明线段和、差或不等关系的常用方法,用这两种方法解题的关键是通过截长法或补短法构造全等三角形,将分散的和差线段转化为同一直线上的和差线段.
专训三
1.解:因为∠ACB=90°,
所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD.
(第2题)
2.解:可设计如图所示的工具,其中AC=BD,O为AC,BD的中点.
在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以AB=CD,即CD的长就是A,B间的距离.测出CD的长为b.
因为AB=a-2x,所以x==.
3.解:三个石凳E,M,F恰好在一条直线上.
理由:分别连接EM,MF.
∵AB∥CD,∴∠B=∠C,
∵M是BC的中点,∴BM=CM,
在△BEM和△CFM中,
∴△BEM≌△CFM(SAS).
∴∠BME=∠CMF.
又∵∠BMF+∠CMF=180°,
∴∠BMF+∠BME=180°.
∴三个石凳E,M,F恰好在一条直线上.
4.解:在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以∠AOB=∠COD.
又因为∠AOB+∠BOC=180°,
所以∠BOC+∠COD=180°,
即∠BOD=180°.所以D,O,B三点在同一条直线上.
所以钻头沿着DO的方向打孔,一定从点B处打出.
专训四
1.D
2.70°;15 cm
3.解:∵∠CAD=15°,∠ACB=105°,
∴∠AFC=∠ACB-∠CAD=105°-15°=90°.
∴∠DFB=180°-∠AFC=180°-90°=90°.
∵△ABC≌△ADE,
∴∠ABC=∠ADE=25°.
∴∠CAB=180°-(∠ABC+∠ACB)=180°-(25°+105°)=50°.
∴∠DAE=∠CAB=50°.
∴∠G=180°-90°-50°=40°.
4.B
5.∠ACB=∠DCE或∠BCE=∠ACD或∠B=∠E
6.证明:∵AB∥CE,∴∠BAC=∠DCE.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA).
7.C
8.证明:连接AD.∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD,∴∠ABD=∠ACD,
∴∠DCF=∠DBE.
又∵∠DFC=∠DEB=90°,DC=DB.
∴△DFC≌△DEB,∴DF=DE.
9.(1)证明:∵CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.
在△BCD和△FCE中.
∴△BCD≌△FCE.
(2)解:由△BCD≌△FCE,得∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°.
∴∠BDC=90°.
10.解:(1)可行;满足边角边判定法可判定△ABC≌△DEC,因而AB=DE
(2)可行;满足角边角判定法,可判定△ABC≌△EDC,因而AB=DE
(3)使∠ABC=∠EDC;成立.
(第11题)
11.证明:如图,分别取AD,BC的中点N,M,连接BN,CN,MN,则有AN=ND,BM=MC.
在△ABN和△DCN中,
∴△ABN≌△DCN(SAS).
∴∠ABN=∠DCN,NB=NC.
在△NBM和△NCM中,
∴△NBM≌△NCM(SSS).
∴∠NBC=∠NCB.
∴∠NBC+∠ABN=∠NCB+∠DCN,
即∠ABC=∠DCB.
点拨:添加辅助线构造全等三角形是常用的解题方法,辅助线的添加以能创造已知条件为上策,如本题取AD,BC的中点就是把中点作为已知条件,构造全等三角形,将证明角相等,转化为证明三角形全等,分散证明,体现了转化思想的运用.
12.解:∵D为AB的中点,AB=10 cm,∴BD=AD=5 cm.设点P运动的时间是x s,则BP=CQ=3x cm,CP=(8-3x)cm.若BD与CQ是对应边,则BD=CQ,∴5=3x,解得x=,此时BP=3×=5(cm),CP=8-5=3(cm),BP≠CP,故舍去;若BD与CP是对应边,则BD=CP,∴5=8-3x,解得x=1,符合题意.综上,点P运动的时间是1 s.
点拨:由∠B=∠C可知DP与PQ是对应边,而其他两组对应边的对应关系不确定,因此要分BD与CQ是对应边、BD与CP是对应边两种情况考虑,体现了分类讨论思想的运用.
(第13题)
13.解:(1)相等.证明:如图,作DG⊥AB,DH⊥AC,垂足分别为G,H.
∵AD是∠BAC的平分线,
∴∠DAG=∠DAH,∵DG⊥AB,DH⊥AC,
∴∠AGD=∠AHD=90°,
又∵AD=AD,
∴△AGD≌△AHD,
∴DG=DH.
∵∠AED+∠AFD=180°,
∠DFH+∠AFD=180°,
∴∠AED=∠DFH.
在△GDE和△HDF中,
∴△GDE≌△HDF.∴DE=DF.
(2)成立.
点拨:本题运用了类比思想,由题图(1)联想到题图(2)辅助线的作法.探究中的两个小题只是交换了已知和结论,考虑(2)题时要在(1)题的基础上逆向思考.
名师点金:全等三角形的性质和判定是初中数学的重点内容,也是学习其他几何知识的基础,三角形全等的判定和性质是证明线段相等、角相等的重要依据,并由此还可以获得直线之间的垂直(平行)关系,线段(面积)的和、差、倍、分关系.
位置关系
1.如图,已知BE⊥AC,CF⊥AB,BM=AC,CN=AB.求证:AM⊥AN.
(第1题)
相等关系
2.(2015·珠海)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.
(1)如图①,连接BD,AF,则BD________AF.(填“>”,“<”或“=”号)
(2)如图②,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF.求证:BH=GF.
(第2题)
和差关系
3.如图,∠BCA=α,CA=CB,C,E,F分别是直线CD上的三点,且∠BEC=∠CFA=α,请提出对EF,BE,AF三条线段之间数量关系的合理猜想,并证明.
(第3题)
倍数关系
4.如图,在Rt△ABC中,∠ABC=∠A,∠ACB=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.
当∠EDF绕点D旋转到DE⊥AC于点E时,如图①,易证S△DEF+S△CEF=S△ABC;当∠EDF绕点D旋转到DE和AC不垂直时,在图②和图③这两种情况下,上述结论是否仍成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?请写出你的猜想,不需证明.
(第4题)
专训二:构造全等三角形的六种常用方法
名师点金:在进行几何题的证明或计算时,需要在图形中添加一些辅助线,辅助线能使题目中的条件比较集中,能比较容易找到一些量之间的关系,使数学问题较轻松地解决.常见的辅助线作法有:构造法、平行线法、旋转法、翻折法、倍长中线法和截长补短法,目的都是构造全等三角形.
翻折法
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.
(第1题)
构造法
2.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.
求证:∠ADC=∠BDF.
(第2题)
旋转法
3.如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
(第3题)
平行线法
4.在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC交AC于点Q,且AP与BQ相交于点O.求证:AB+BP=BQ+AQ.
(第4题)
倍长中线法
5.如图,在△ABC中,D为BC的中点.
(1)求证:AB+AC>2AD;
(2)若AB=5,AC=3,求AD的取值范围.
(第5题)
截长补短法
6.如图,AB∥CD,CE,BE分别平分∠BCD和∠CBA,点E在AD上.求证:BC=AB+CD.
(第6题)
专训三:全等三角形的四种常见实际应用
名师点金:利用三角形全等解决实际问题的步骤:
(1)明确应用哪些知识来解决实际问题;(2)根据实际问题抽象出几何图形;
(3)结合图形和题意分析已知条件;(4)找到已知与未知的联系,寻求恰当的解决途径,并表述清楚.
利用三角形全等测量池塘两端的距离
1.如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
(第1题)
利用三角形全等测量物体的内径
2.如图,已知零件的外径为a,要求它的厚度x,动手制作一个简单的工具,利用三角形全等的知识,求出x.
(第2题)
利用三角形全等判断三点是否共线
3.如图,公园里有一条“Z”形道路ABCD,其中AB∥CD,在AB,BC,CD三段路路旁各有一个石凳E,M,F,且BE=CF,石凳M在BC的中点处,试判断三个石凳E,M,F是否恰好在一条直线上?为什么?
(第3题)
利用三角形全等解决工程中的问题
4.如图,工人师傅要在墙壁的点O处用钻打孔,要使孔口从墙壁对面的点B处打开,墙壁厚35 cm,点B与点O的垂直距离AB长20 cm,在点O处作一直线平行于地面,再在直线上截取OC=35 cm,过点C作OC的垂线,在垂线上截取CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从点B处打出,这是什么道理?
(第4题)
专训四:几类常见的热门考点
名师点金:本章主要学习了全等三角形的性质与判定,其考查形式有利用全等三角形证明线段或角的数量关系,求线段的长度或角的度数,判断位置关系,以及利用全等三角形解决实际问题等.
全等三角形的性质
1.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式中不正确的是( )
(第1题)
A.AB=AC
B.∠BAE=∠CAD
C.BD=CE
D.AD=DE
2.已知△ABC≌△A′B′C′,∠A=∠A′=50°,∠B=∠B′=60°,AB=15 cm,则∠C′的度数为________,A′B′的长度为________.
3.如图,已知△ABC≌△ADE,BC边的延长线交AD于点F,交AE的延长线于点G,∠ACB=105°,∠CAD=15°,∠ADE=25°,求∠DFB和∠G的度数.
(第3题)
全等三角形的判定
4.在△ABC和△A′B′C′中,下列各组条件中,不能判定△ABC≌△A′B′C′的是( )
①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′.
A.具备①②③ B.具备①②④
C.具备③④⑤ D.具备②③⑥
(第5题)
5.如图,已知BC=EC,∠A=∠D,要使△ABC≌△DEC,则应添加的一个条件为________(只需填一个).
6.(中考·宁德)如图所示,点D,A,C在同一直线上,AB∥CE,AB=CD,∠B=∠D.
求证:△ABC≌△CDE.
(第6题)
全等三角形的性质与判定的综合应用
7.如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的是( )
(第7题)
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠DAE=40°
D.∠C=30°
8.(2014·黄冈)如图所示,AB=AC,BD=CD,DE⊥AB交AB的延长线于点E,DF⊥AC交AC的延长线于点F.求证:DE=DF.
(第8题)
9.如图,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(第9题)
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
全等三角形在实际问题中的应用
10.某校七(3)班学生到野外活动,为测量一池塘两端A,B之间的距离,设计了如下方案:
方案一:如图①,先在平地上取一个可以直接到达A,B的点C,连接AC,BC,并延长AC到点D,延长BC到点E,使DC=AC,EC=BC,最后测出DE的长即为A,B之间的距离.
(第10题)
方案二:如图②,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,测出DE的长即为A,B之间的距离.
阅读后回答下列问题:
(1)方案一是否切实可行?________,理由是________________________________________________________________________
________________________________________________________________________.
(2)方案二是否切实可行?________,理由是________________________________________________________________________
________________________________________________________________________.
(3)方案二中作BF⊥AB,ED⊥BF的目的是__________________________;若∠ABD=∠BDE,但不一定垂直,方案二是否成立?__________________.
数学思想方法的应用
a.转化思想
11.如图,AB=DC,∠A=∠D.求证:∠ABC=∠DCB.
(第11题)
b.分类讨论思想
12.如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点.点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
(第12题)
c.类比思想
13.在△ABC中,若AD是∠BAC的平分线,E点和F点分别在AB和AC上,且DE⊥AB,垂足为E,DF⊥AC,垂足为F,如图①,则可以得到以下两个结论:①∠AED+∠AFD=180°;②DE=DF.那么在△ABC中,仍然有条件“AD是∠BAC的平分线,点E和点F分别在AB和AC上”,请探究以下两个问题:
(1)若∠AED+∠AFD=180°,如图②,则DE与DF是否仍相等?若仍相等,请证明;否则请说明理由.
(2)若DE=DF,则∠AED+∠AFD=180°是否成立?(只写出结论,不证明)
(第13题)
答案
专训一
1.证明:如图,∵BE⊥AC,CF⊥AB,∴∠1+∠BAC=90°,∠2+∠BAC=90°.∴∠1=∠2.又∵BM=CA,AB=NC,∴△ABM≌△NCA.∴∠3=∠N.
∵∠N+∠4=90°,∴∠3+∠4=90°,即∠MAN=90°.∴AM⊥AN.
(第1题)
(第2题)
2.(1)=
(2)证明:将△DEF沿FE方向平移,使点E与点C重合,设ED平移后与MN相交于R,如图,
∵MN∥BC,RC∥EH,
∴∠GRC=∠RHE=∠DEF,∠RGC=∠GCB,
易得∠GRC=∠RGC,过点C作CZ⊥GR,∴∠CZR=∠CZG=90°,
又∵CZ=CZ,∴△CZR≌△CZG,
∴CR=CG.
又∵MN∥BF,CR∥EH,∴四边形RCEH为平行四边形,∴CR=EH.∴CG=HE.
由平移的性质得BC=EF,
∴BC+CE=CE+EF,即BE=CF.
易得∠HEB=∠GCF,∴△BEH≌△FCG(SAS),
∴BH=FG.
3.解:猜想:EF=BE+AF.
证明:∵∠BCE+∠CBE+∠BEC=180°,
∠BCE+∠ACF+∠BCA=180°,
∠BCA=α=∠BEC,
∴∠CBE=∠ACF.
又∵∠BEC=∠CFA=α,CB=AC,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.∴EF=CF+EC=BE+AF.
(第4题)
4.解:在题图(2)中结论仍成立;在题图(3)中不成立.
对于题图(2)证明如下:
如图,过点D作DM⊥AC,DN⊥BC,垂足分别为M,N,
则∠DME=∠DNF=∠MDN=90°.
又∵∠A=∠ABC,∠AMD=∠BND=90°,
且易知DA=DB,
∴△ADM≌△BDN,∴DM=DN.
∵∠MDE+∠EDN=∠MDN=90°,∠EDN+∠NDF=∠EDF=90°,
∴∠MDE=∠NDF.
∴△DME≌△DNF.
∴S四边形DMCN=S四边形DECF=S△DEF+S△CEF.由题图(1)可知S四边形DMCN=S△ABC,∴S△DEF+S△CEF=S△ABC.
在题图(3)中,S△DEF,S△CEF,S△ABC之间的关系是S△DEF-S△CEF=S△ABC.
专训二
1.证明:如图,延长AD交BC于点F.(相当于将AB边向下翻折,与BC边重合,A点落在F点处,折痕为BE)
∵BE平分∠ABC,∴∠ABE=∠CBE.
∵BD⊥AD,∴∠ADB=∠BDF=90°.
在△ABD和△FBD中,
∴△ABD≌△FBD(ASA).
∴∠2=∠DFB.
又∵∠DFB=∠1+∠C,∴∠2=∠1+∠C.
(第1题)
(第2题)
2.证明:如图,过点B作BG⊥BC交CF的延长线于点G.
∵∠ACB=90°,∴∠2+∠ACF=90°.
∵CE⊥AD,∴∠AEC=90°,∴∠1+∠ACF=180°-∠AEC=180°-90°=90°.∴∠1=∠2.
在△ACD和△CBG中,
∴△ACD≌△CBG(ASA).
∴∠ADC=∠G,CD=BG.
∵点D为BC的中点,∴CD=BD.∴BD=BG.
又∵∠DBG=90°,∠DBF=45°,∴∠GBF=∠DBG-∠DBF=90°-45°=45°.∴∠DBF=∠GBF.
在△BDF和△BGF中,
∴△BDF≌△BGF(SAS).
∴∠BDF=∠G.∴∠ADC=∠BDF.
点拨:本题运用了构造法,通过作辅助线构造△CBG、△BGF是解题的关键.
3.解:如图,延长CB到点H,使得BH=DF,连接AH.
∵∠ABE=90°,∠D=90°,∴∠D=∠ABH=90°.
在△ABH和△ADF中,
∴△ABH≌△ADF.∴AH=AF,∠BAH=∠DAF.
∴∠BAH+∠BAF=∠DAF+∠BAF,即∠HAF=∠BAD=90°.
∵BE+DF=EF,∴BE+BH=EF,即HE=EF.
在△AEH和△AEF中,
(第3题)
∴△AEH≌△AEF.
∴∠EAH=∠EAF.
∴∠EAF=∠HAF=45°.
点拨:图中所作辅助线,相当于将△ADF绕点A顺时针旋转90°,使AD边与AB边重合,得到△ABH.
4.证明:过点O作OD∥BC交AB于点D,
∴∠ADO=∠ABC.∵∠BAC=60°,∠C=40°,
∴∠ABC=80°.∴∠ADO=80°.
∵BQ平分∠ABC,∴∠QBC=40°.∴∠AQB=∠C+∠QBC=80°.∴∠ADO=∠AQB.
易知∠DAO=∠QAO,OA=OA,∴△ADO≌△AQO.
∴OD=OQ,AD=AQ.
又∵OD∥BP,∴∠PBO=∠DOB.
又∵∠PBO=∠DBO,∴∠DBO=∠DOB.
∴过点D作DM⊥BQ,∴∠DMB=∠DMO=90°.
又∵DM=DM,∴△DMB≌△DMO.
∴BD=OD.∴BD=OQ.
∵∠BAC=60°,∠ABC=80°,BQ平分∠ABC,AP平分∠BAC,∴∠BAP=30°,∠ABQ=40°,∴∠BOP=70°.
∵∠BAP=30°,∠ABC=80°,∴∠APB=70°.
∴∠BOP=∠APB,过点B作BN⊥OP,
∴∠BNO=∠BNP=90°,
又∵BN=BN,∴△BNO≌△BNP.
∴BO=BP.∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ.
5.(1)证明:延长AD至点E,使DE=AD,连接BE.
∵D为BC的中点,∴CD=BD.
又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.
∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
(2)解:∵AB-BE
6.证明:方法一:如图①,在BC上取一点F,使BF=BA.连接EF.∵CE,BE分别平分∠BCD和∠CBA,∴∠3=∠4,∠1=∠2.
在△ABE和△FBE中,
∴△ABE≌△FBE(SAS).∴∠A=∠5.
∵AB∥CD,∴∠A+∠D=180°.
而∠5+∠6=180°,∴∠6=∠D.
在△EFC和△EDC中,
∴△EFC≌△EDC(AAS),
∴FC=DC.∴BC=BF+CF=AB+CD.
(第6题)
方法二:如图②,分别延长BA,CE交于点F.
∵AB∥CD,∴∠ABC+∠BCD=180°.
∵CE,BE分别平分∠BCD和∠CBA,
∴∠1=∠2=∠ABC,∠3=∠4=∠BCD.
∴∠2+∠3=(∠ABC+∠BCD)=90°.
∴∠BEC=90°.∴∠BEF=∠BEC=90°.
在△BEC和△BEF中,
∴△BEC≌△BEF(ASA).∴BC=BF,EC=EF.
∵AB∥CD,∴∠7=∠D,∠F=∠4.
在△EAF和△EDC中,
∴△EAF≌△EDC(AAS).∴FA=CD.
∴BC=BF=BA+AF=AB+CD.
点拨:本题运用了两种不同的方法解题,方法一是截长法,方法二是补短法,这两种方法都是证明线段和、差或不等关系的常用方法,用这两种方法解题的关键是通过截长法或补短法构造全等三角形,将分散的和差线段转化为同一直线上的和差线段.
专训三
1.解:因为∠ACB=90°,
所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD.
(第2题)
2.解:可设计如图所示的工具,其中AC=BD,O为AC,BD的中点.
在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以AB=CD,即CD的长就是A,B间的距离.测出CD的长为b.
因为AB=a-2x,所以x==.
3.解:三个石凳E,M,F恰好在一条直线上.
理由:分别连接EM,MF.
∵AB∥CD,∴∠B=∠C,
∵M是BC的中点,∴BM=CM,
在△BEM和△CFM中,
∴△BEM≌△CFM(SAS).
∴∠BME=∠CMF.
又∵∠BMF+∠CMF=180°,
∴∠BMF+∠BME=180°.
∴三个石凳E,M,F恰好在一条直线上.
4.解:在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以∠AOB=∠COD.
又因为∠AOB+∠BOC=180°,
所以∠BOC+∠COD=180°,
即∠BOD=180°.所以D,O,B三点在同一条直线上.
所以钻头沿着DO的方向打孔,一定从点B处打出.
专训四
1.D
2.70°;15 cm
3.解:∵∠CAD=15°,∠ACB=105°,
∴∠AFC=∠ACB-∠CAD=105°-15°=90°.
∴∠DFB=180°-∠AFC=180°-90°=90°.
∵△ABC≌△ADE,
∴∠ABC=∠ADE=25°.
∴∠CAB=180°-(∠ABC+∠ACB)=180°-(25°+105°)=50°.
∴∠DAE=∠CAB=50°.
∴∠G=180°-90°-50°=40°.
4.B
5.∠ACB=∠DCE或∠BCE=∠ACD或∠B=∠E
6.证明:∵AB∥CE,∴∠BAC=∠DCE.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA).
7.C
8.证明:连接AD.∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD,∴∠ABD=∠ACD,
∴∠DCF=∠DBE.
又∵∠DFC=∠DEB=90°,DC=DB.
∴△DFC≌△DEB,∴DF=DE.
9.(1)证明:∵CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.
在△BCD和△FCE中.
∴△BCD≌△FCE.
(2)解:由△BCD≌△FCE,得∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°.
∴∠BDC=90°.
10.解:(1)可行;满足边角边判定法可判定△ABC≌△DEC,因而AB=DE
(2)可行;满足角边角判定法,可判定△ABC≌△EDC,因而AB=DE
(3)使∠ABC=∠EDC;成立.
(第11题)
11.证明:如图,分别取AD,BC的中点N,M,连接BN,CN,MN,则有AN=ND,BM=MC.
在△ABN和△DCN中,
∴△ABN≌△DCN(SAS).
∴∠ABN=∠DCN,NB=NC.
在△NBM和△NCM中,
∴△NBM≌△NCM(SSS).
∴∠NBC=∠NCB.
∴∠NBC+∠ABN=∠NCB+∠DCN,
即∠ABC=∠DCB.
点拨:添加辅助线构造全等三角形是常用的解题方法,辅助线的添加以能创造已知条件为上策,如本题取AD,BC的中点就是把中点作为已知条件,构造全等三角形,将证明角相等,转化为证明三角形全等,分散证明,体现了转化思想的运用.
12.解:∵D为AB的中点,AB=10 cm,∴BD=AD=5 cm.设点P运动的时间是x s,则BP=CQ=3x cm,CP=(8-3x)cm.若BD与CQ是对应边,则BD=CQ,∴5=3x,解得x=,此时BP=3×=5(cm),CP=8-5=3(cm),BP≠CP,故舍去;若BD与CP是对应边,则BD=CP,∴5=8-3x,解得x=1,符合题意.综上,点P运动的时间是1 s.
点拨:由∠B=∠C可知DP与PQ是对应边,而其他两组对应边的对应关系不确定,因此要分BD与CQ是对应边、BD与CP是对应边两种情况考虑,体现了分类讨论思想的运用.
(第13题)
13.解:(1)相等.证明:如图,作DG⊥AB,DH⊥AC,垂足分别为G,H.
∵AD是∠BAC的平分线,
∴∠DAG=∠DAH,∵DG⊥AB,DH⊥AC,
∴∠AGD=∠AHD=90°,
又∵AD=AD,
∴△AGD≌△AHD,
∴DG=DH.
∵∠AED+∠AFD=180°,
∠DFH+∠AFD=180°,
∴∠AED=∠DFH.
在△GDE和△HDF中,
∴△GDE≌△HDF.∴DE=DF.
(2)成立.
点拨:本题运用了类比思想,由题图(1)联想到题图(2)辅助线的作法.探究中的两个小题只是交换了已知和结论,考虑(2)题时要在(1)题的基础上逆向思考.
