沪科版八年级上册数学 第14章全等三角形 14.2.6三角形全等的判定综合应用 阶段强化专训 学案(word版含答案)
文档属性
| 名称 | 沪科版八年级上册数学 第14章全等三角形 14.2.6三角形全等的判定综合应用 阶段强化专训 学案(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览



文档简介
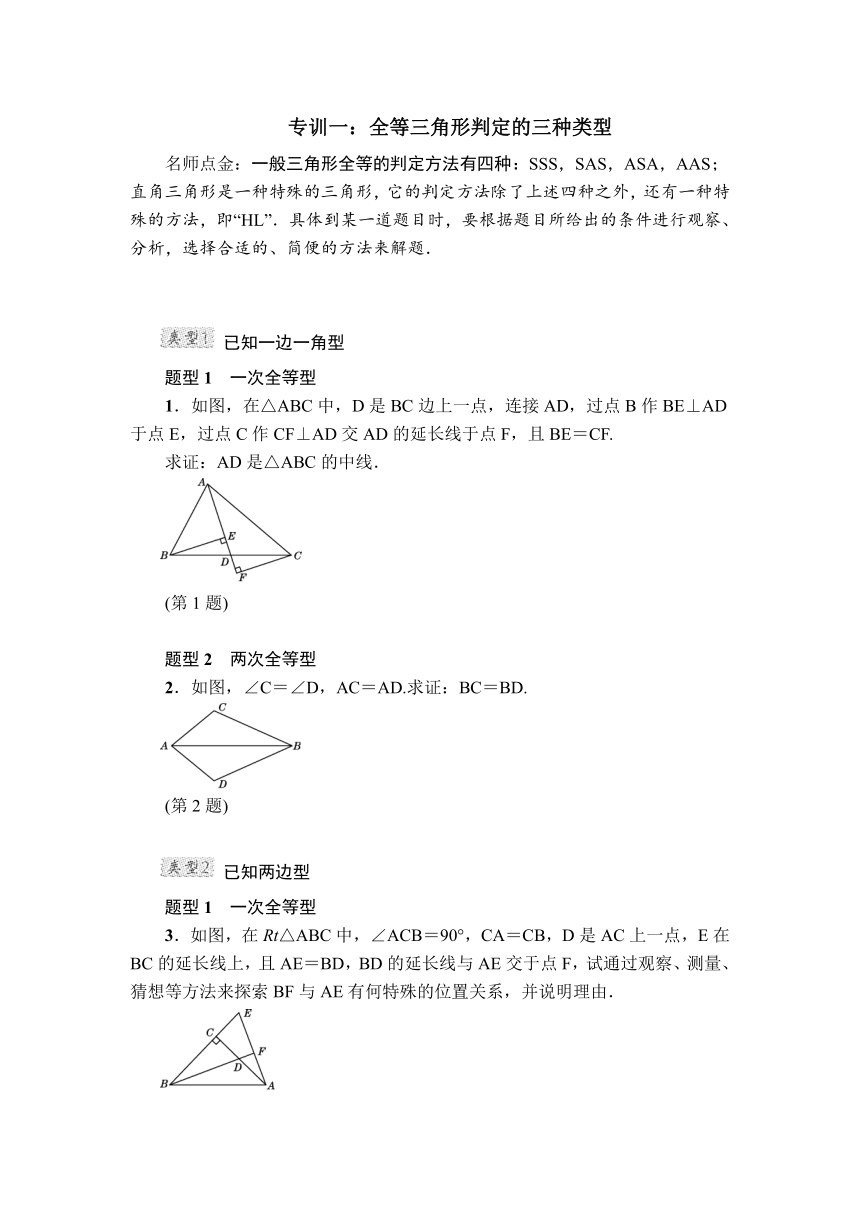
专训一:全等三角形判定的三种类型
名师点金:一般三角形全等的判定方法有四种:SSS,SAS,ASA,AAS;直角三角形是一种特殊的三角形,它的判定方法除了上述四种之外,还有一种特殊的方法,即“HL”.具体到某一道题目时,要根据题目所给出的条件进行观察、分析,选择合适的、简便的方法来解题.
已知一边一角型
题型1 一次全等型
1.如图,在△ABC中,D是BC边上一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.
求证:AD是△ABC的中线.
(第1题)
题型2 两次全等型
2.如图,∠C=∠D,AC=AD.求证:BC=BD.
(第2题)
已知两边型
题型1 一次全等型
3.如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F,试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明理由.
(第3题)
题型2 两次全等型
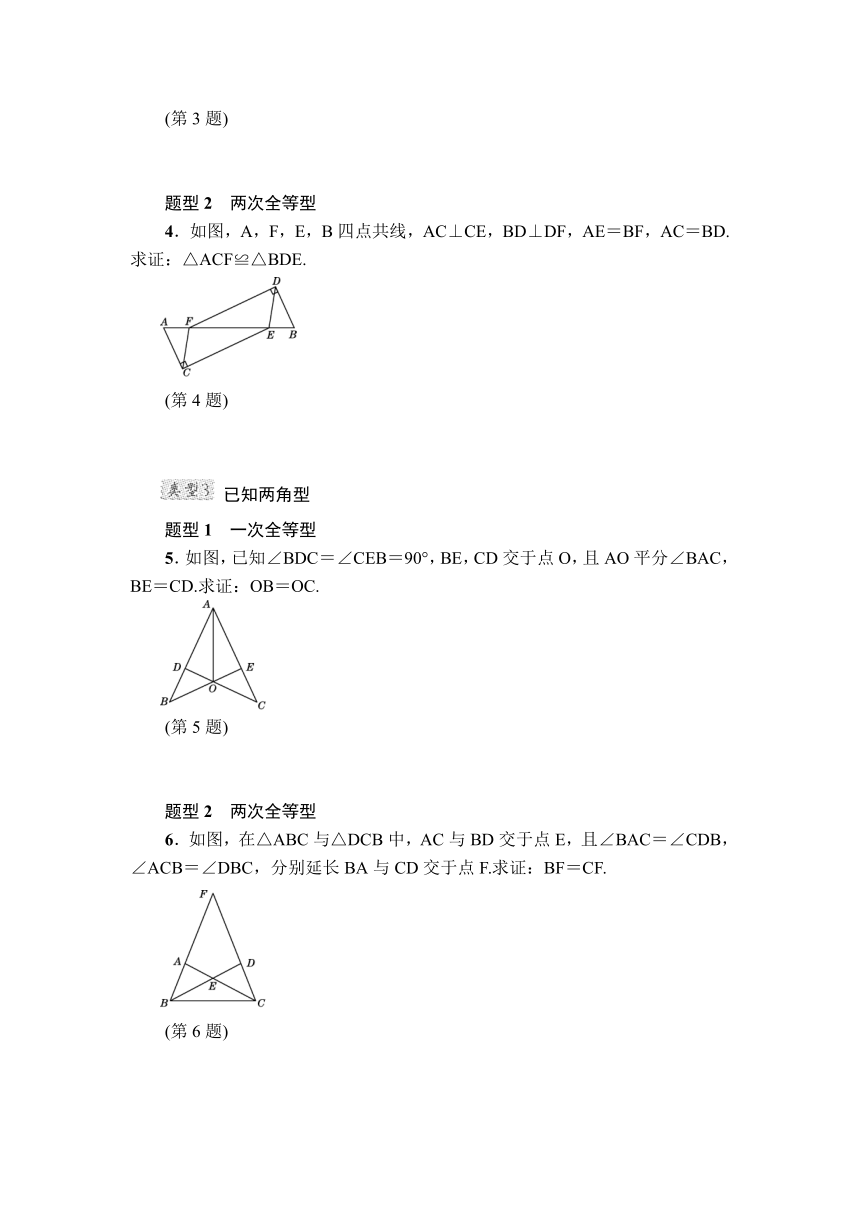
4.如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:△ACF≌△BDE.
(第4题)
已知两角型
题型1 一次全等型
5.如图,已知∠BDC=∠CEB=90°,BE,CD交于点O,且AO平分∠BAC,BE=CD.求证:OB=OC.
(第5题)
题型2 两次全等型
6.如图,在△ABC与△DCB中,AC与BD交于点E,且∠BAC=∠CDB,∠ACB=∠DBC,分别延长BA与CD交于点F.求证:BF=CF.
(第6题)
专训二:证明三角形全等的四种思路
名师点金:全等三角形是初中几何的重要内容之一,是几何入门最关键的一步,学习了判定三角形全等的几种方法之后,如何根据已知条件证明三角形全等,掌握证明全等的几种思路尤为重要.
条件充足时直接用判定方法
1.(2014·武汉)如图,AC和BD相交于点O,OA=OC,OB=OD.求证:AB∥CD.
(第1题)
条件不足时添加条件再用判定方法
2.(改编·衡阳)如图,点A,F,C,D在一条直线上,AF=DC,BC∥EF,请只补充一个条件,使得△ABC≌△DEF,并说明理由.
(第2题)
非三角形问题中构造全等三角形用判定方法
3.如图,在四边形OACB中,CM⊥OA于M,∠1=∠2,CA=CB.求证:
(1)∠3+∠4=180°;
(2)OA+OB=2OM.
(第3题)
实际问题中建立全等三角形模型用判定方法
4.如图,要测量AB的长,因为无法过河接近点A,可以在AB所在直线外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一条直线上,则HG=AB,试说明理由.
(第4题)
答案
专训一
1.证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.
又∵∠BDE=∠CDF,BE=CF,∴△DBE≌△DCF.
∴BD=CD.∴D是BC的中点,即AD是△ABC的中线.
2.证明:过点A作AM⊥BC,AN⊥BD,分别交BC,BD的延长线于点M,N.∴∠M=∠N=90°.
∵∠ACB=∠ADB,∴∠ACM=∠ADN.
在△ACM和△ADN中,
∴△ACM≌△ADN(AAS).∴AM=AN,CM=DN.
在Rt△ABM和Rt△ABN中,
∴Rt△ABM≌Rt△ABN(HL).
∴BM=BN.∴BM-CM=BN-DN,即BC=BD.
3.解:BF⊥AE.理由如下:
∵∠ACB=90°,∴∠ACE=∠BCD=90°.
又∵BC=AC,BD=AE,∴Rt△BDC≌Rt△AEC(HL).
∴∠CBD=∠CAE.
又∵∠CAE+∠E=90°,∴∠EBF+∠E=90°.
∴∠BFE=90°,即BF⊥AE.
4.证明:∵AC⊥CE,BD⊥DF,∴∠ACE=∠BDF=90°.
在Rt△ACE和Rt△BDF中,
∴Rt△ACE≌Rt△BDF(HL).∴∠A=∠B.
∵AE=BF,∴AE-EF=BF-EF,即AF=BE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
5.证明:∵∠BDC=∠CEB=90°,
∴∠ADO=∠AEO=90°.
∵AO平分∠BAC,∴∠DAO=∠EAO.
在△ADO和△AEO中,
∴△ADO≌△AEO(AAS).
∴OD=OE.
又∵CD=BE,∴CD-OD=BE-OE,即OC=OB.
6.证明:在△ABC和△DCB中,
∴△ABC≌△DCB(AAS).∴AC=DB.
又∵∠BAC=∠CDB,∴∠FAC=∠FDB.
在△FAC和△FDB中,
∴△FAC≌△FDB(AAS).∴CF=BF.
专训二
1.证明:在△AOB和△COD中,
∴△AOB≌△COD.∴∠A=∠C.
∴AB∥CD.
2.解:补充条件:EF=BC,可使得△ABC≌△DEF.
理由如下:
∵AF=DC,点A,F,C,D在一条直线上,
∴AF+FC=DC+FC,即AC=DF.
∵BC∥EF,∴∠EFD=∠BCA.
在△DEF和△ABC中,
∴△DEF≌△ABC(SAS).
点拨:答案不唯一.
(第3题)
3.证明:如图,过C点作CE⊥OB,交OB的延长线于E点.
(1)∵CM⊥OA,CE⊥OE,
∴∠OEC=∠OMC=90°,
在△OEC和△OMC中,
∴△OEC≌△OMC(AAS).
∴CE=CM,又∵CA=CB,
∴Rt△BCE≌Rt△ACM(HL).
∴∠3=∠CBE,
∴∠3+∠4=∠CBE+∠4=180°.
(2)由(1)知△OCE≌△OCM,
Rt△BCE≌Rt△ACM,
∴OE=OM,BE=AM,
∴OA+OB=OM+AM+OB=OM+BE+OB=OM+OE=2OM.
4.解:在△DEB和△DFG中,
∵DB=DG,∠BDE=∠GDF,DE=DF,
∴△DEB≌△DFG(SAS).
∴∠E=∠F,∴AE∥FH,
∴∠DBA=∠DGH.
又∵DB=DG,∠ADB=∠HDG.
∴△ADB≌△HDG(ASA),
∴AB=HG.
名师点金:一般三角形全等的判定方法有四种:SSS,SAS,ASA,AAS;直角三角形是一种特殊的三角形,它的判定方法除了上述四种之外,还有一种特殊的方法,即“HL”.具体到某一道题目时,要根据题目所给出的条件进行观察、分析,选择合适的、简便的方法来解题.
已知一边一角型
题型1 一次全等型
1.如图,在△ABC中,D是BC边上一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.
求证:AD是△ABC的中线.
(第1题)
题型2 两次全等型
2.如图,∠C=∠D,AC=AD.求证:BC=BD.
(第2题)
已知两边型
题型1 一次全等型
3.如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F,试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明理由.
(第3题)
题型2 两次全等型
4.如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:△ACF≌△BDE.
(第4题)
已知两角型
题型1 一次全等型
5.如图,已知∠BDC=∠CEB=90°,BE,CD交于点O,且AO平分∠BAC,BE=CD.求证:OB=OC.
(第5题)
题型2 两次全等型
6.如图,在△ABC与△DCB中,AC与BD交于点E,且∠BAC=∠CDB,∠ACB=∠DBC,分别延长BA与CD交于点F.求证:BF=CF.
(第6题)
专训二:证明三角形全等的四种思路
名师点金:全等三角形是初中几何的重要内容之一,是几何入门最关键的一步,学习了判定三角形全等的几种方法之后,如何根据已知条件证明三角形全等,掌握证明全等的几种思路尤为重要.
条件充足时直接用判定方法
1.(2014·武汉)如图,AC和BD相交于点O,OA=OC,OB=OD.求证:AB∥CD.
(第1题)
条件不足时添加条件再用判定方法
2.(改编·衡阳)如图,点A,F,C,D在一条直线上,AF=DC,BC∥EF,请只补充一个条件,使得△ABC≌△DEF,并说明理由.
(第2题)
非三角形问题中构造全等三角形用判定方法
3.如图,在四边形OACB中,CM⊥OA于M,∠1=∠2,CA=CB.求证:
(1)∠3+∠4=180°;
(2)OA+OB=2OM.
(第3题)
实际问题中建立全等三角形模型用判定方法
4.如图,要测量AB的长,因为无法过河接近点A,可以在AB所在直线外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一条直线上,则HG=AB,试说明理由.
(第4题)
答案
专训一
1.证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.
又∵∠BDE=∠CDF,BE=CF,∴△DBE≌△DCF.
∴BD=CD.∴D是BC的中点,即AD是△ABC的中线.
2.证明:过点A作AM⊥BC,AN⊥BD,分别交BC,BD的延长线于点M,N.∴∠M=∠N=90°.
∵∠ACB=∠ADB,∴∠ACM=∠ADN.
在△ACM和△ADN中,
∴△ACM≌△ADN(AAS).∴AM=AN,CM=DN.
在Rt△ABM和Rt△ABN中,
∴Rt△ABM≌Rt△ABN(HL).
∴BM=BN.∴BM-CM=BN-DN,即BC=BD.
3.解:BF⊥AE.理由如下:
∵∠ACB=90°,∴∠ACE=∠BCD=90°.
又∵BC=AC,BD=AE,∴Rt△BDC≌Rt△AEC(HL).
∴∠CBD=∠CAE.
又∵∠CAE+∠E=90°,∴∠EBF+∠E=90°.
∴∠BFE=90°,即BF⊥AE.
4.证明:∵AC⊥CE,BD⊥DF,∴∠ACE=∠BDF=90°.
在Rt△ACE和Rt△BDF中,
∴Rt△ACE≌Rt△BDF(HL).∴∠A=∠B.
∵AE=BF,∴AE-EF=BF-EF,即AF=BE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
5.证明:∵∠BDC=∠CEB=90°,
∴∠ADO=∠AEO=90°.
∵AO平分∠BAC,∴∠DAO=∠EAO.
在△ADO和△AEO中,
∴△ADO≌△AEO(AAS).
∴OD=OE.
又∵CD=BE,∴CD-OD=BE-OE,即OC=OB.
6.证明:在△ABC和△DCB中,
∴△ABC≌△DCB(AAS).∴AC=DB.
又∵∠BAC=∠CDB,∴∠FAC=∠FDB.
在△FAC和△FDB中,
∴△FAC≌△FDB(AAS).∴CF=BF.
专训二
1.证明:在△AOB和△COD中,
∴△AOB≌△COD.∴∠A=∠C.
∴AB∥CD.
2.解:补充条件:EF=BC,可使得△ABC≌△DEF.
理由如下:
∵AF=DC,点A,F,C,D在一条直线上,
∴AF+FC=DC+FC,即AC=DF.
∵BC∥EF,∴∠EFD=∠BCA.
在△DEF和△ABC中,
∴△DEF≌△ABC(SAS).
点拨:答案不唯一.
(第3题)
3.证明:如图,过C点作CE⊥OB,交OB的延长线于E点.
(1)∵CM⊥OA,CE⊥OE,
∴∠OEC=∠OMC=90°,
在△OEC和△OMC中,
∴△OEC≌△OMC(AAS).
∴CE=CM,又∵CA=CB,
∴Rt△BCE≌Rt△ACM(HL).
∴∠3=∠CBE,
∴∠3+∠4=∠CBE+∠4=180°.
(2)由(1)知△OCE≌△OCM,
Rt△BCE≌Rt△ACM,
∴OE=OM,BE=AM,
∴OA+OB=OM+AM+OB=OM+BE+OB=OM+OE=2OM.
4.解:在△DEB和△DFG中,
∵DB=DG,∠BDE=∠GDF,DE=DF,
∴△DEB≌△DFG(SAS).
∴∠E=∠F,∴AE∥FH,
∴∠DBA=∠DGH.
又∵DB=DG,∠ADB=∠HDG.
∴△ADB≌△HDG(ASA),
∴AB=HG.
