湖南省衡阳市八中11-12学年高二学业水平模拟考试(数学理)
文档属性
| 名称 | 湖南省衡阳市八中11-12学年高二学业水平模拟考试(数学理) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-09 00:00:00 | ||
图片预览


文档简介
衡阳市八中高二学业水平模拟考试(2012.04.)
数 学(理科)
命题:仇武君 审题:钟小霖
本试题卷共三大题21小题,全卷满分100分,考试时量120分钟.请将答案写在答卷上.
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.满足条件{1}={1,2}的集合M的个数是( )
A.1; B.2; C.3; D.4;
2.设集合,满足,则实数的取值范围是( )
A. ; B. ; C. ; D. ;
3.下列四个函数中,在区间上为增函数的是( )
A. ; B. ; C. ; D. ;
4.函数且的图象必经过点( )
A.(0,1); B.(1,1); C.(0,2); D.(2,0);
5.已知,,,,则( )
. . . .
6.若(其中且),则函数与的图象( )
.关于直线对称; .关于轴对称;
.关于轴对称; .关于原点对称;
7.已知函数,则( )
A.; B. ; C. ; D. ;
8.函数恰有三个零点,则的值为( )
A.0 B.2 C.4 D. 不存在
9.下列四种说法中错误的一项是( )
A.算法共有三种逻辑结构:顺序结构、条件结构、循环结构;
B.执行框除了具有赋值功能外,还具有计算功能;
C.用秦九韶算法求函数当时的函数值,则;
D.将十进制数77转化为八进制数为116(8);
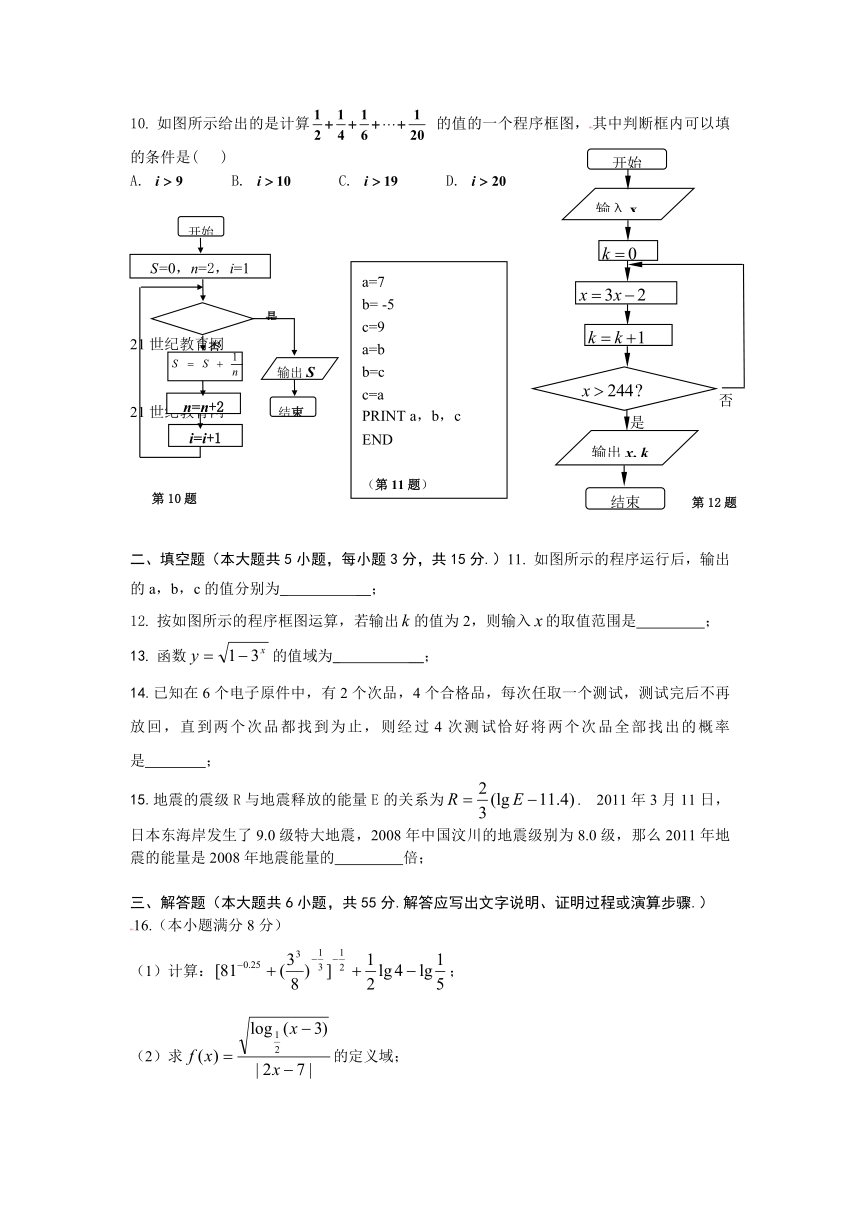
10. 如图所示给出的是计算 的值的一个程序框图,其中判断框内可以填的条件是( )
A. B. C. D.
21世纪教育网
21世纪教育网
二、填空题(本大题共5小题,每小题3分,共15分.)11. 如图所示的程序运行后,输出的a,b,c的值分别为_ __;
12. 按如图所示的程序框图运算,若输出的值为2,则输入的取值范围是 ;
13. 函数的值域为_ __;
14.已知在6个电子原件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将两个次品全部找出的概率是 ;
15.地震的震级R与地震释放的能量E的关系为. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;
三、解答题(本大题共6小题,共55分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分8分)
(1)计算:;
(2)求的定义域;
17.(本小题满分8分)
已知集合,,
(1)若时,求实数的取值范围;
(2)若时,求实数的取值范围;
18.(本小题满分9分)
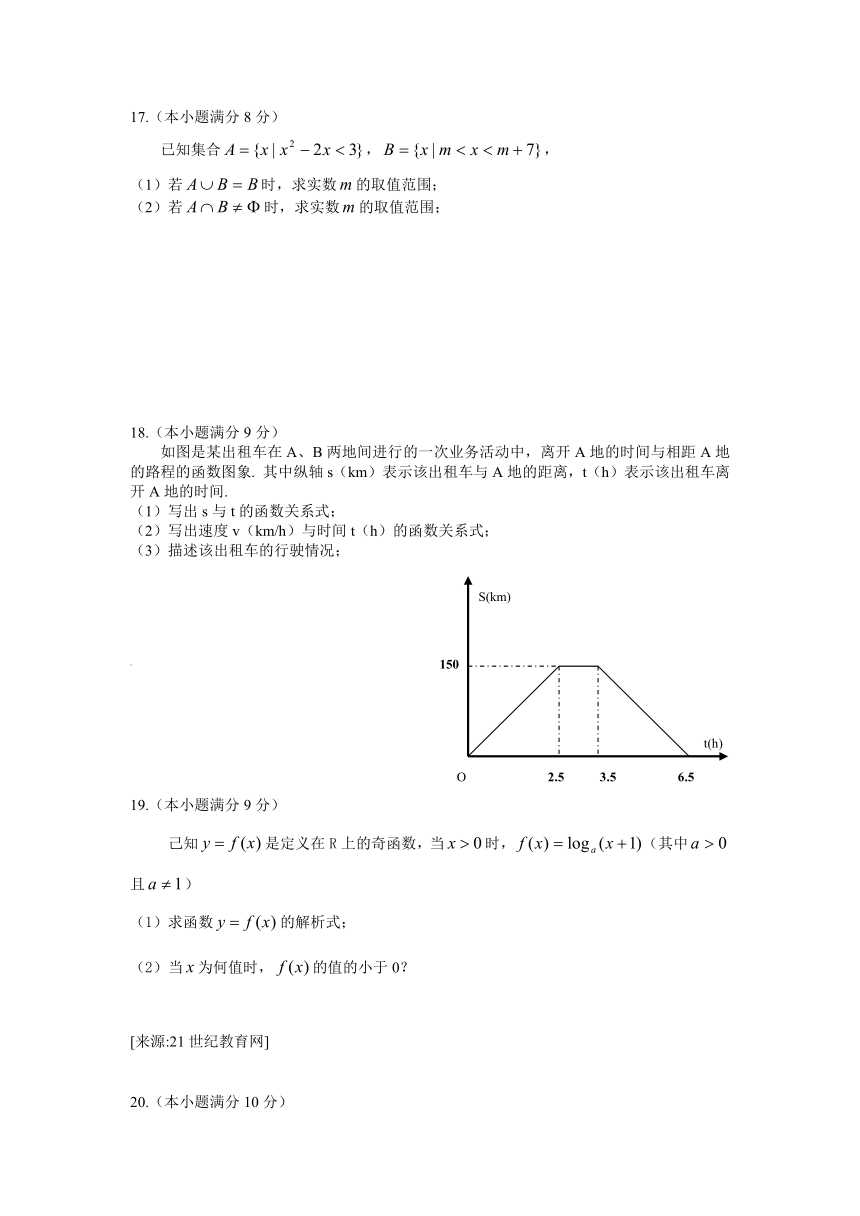
如图是某出租车在A、B两地间进行的一次业务活动中,离开A地的时间与相距A地的路程的函数图象. 其中纵轴s(km)表示该出租车与A地的距离,t(h)表示该出租车离开A地的时间.
(1)写出s与t的函数关系式;
(2)写出速度v(km/h)与时间t(h)的函数关系式;
(3)描述该出租车的行驶情况;
19.(本小题满分9分)
己知是定义在R上的奇函数,当时,(其中且)
(1)求函数的解析式;
(2)当为何值时,的值的小于0?
[来源:21世纪教育网]
20.(本小题满分10分)
某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自独立进行为期一个月的技术攻关,同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为,被乙小组攻克的概率为,
(1)设为攻关期满时获奖的攻关小组数,求的分布列及数学期望;
(2)设为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数在定义域内单调递增”为事件C,求事件C发生的概率;
21.(本小题满分11分)
已知函数,
(1)求函数的定义域;
(2)设,若函数在(2,3)内有且仅有一个零点,求实数的取值范围;
(3)设,求函数在[3,9]内的值域;
衡阳市八中高二学业水平模拟考试(2012.04.)
数 学(理科)(参考答案)
本试题卷共三大题21小题,全卷满分100分,考试时量120分钟.请将答案写在答卷上.[来源:21世纪教育网]
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.满足条件{1}={1,2}的集合M的个数是( B )
A.1; B.2; C.3; D.4;
2.设集合,满足,则实数的取值范围是(C)
A. ; B. ; C. ; D. ;
3.下列四个函数中,在区间上为增函数的是(C )
A. ; B. ; C. ; D. ;
4.函数且的图象必经过点(C)
A.(0,1); B.(1,1); C.(0,2); D.(2,0);
5.已知,,,,则(D)
. . . .
6.若(其中且),则函数与的图象(C)
.关于直线对称; .关于轴对称;
.关于轴对称; .关于原点对称;
7.已知函数,则(A)
A.; B. ; C. ; D. ;
8.函数恰有三个零点,则的值为( C)
A.0 B.2 C.4 D. 不存在
9.下列四种说法中错误的一项是( D)
A.算法共有三种逻辑结构:顺序结构、条件结构、循环结构;
B.执行框除了具有赋值功能外,还具有计算功能;
C.用秦九韶算法求函数当时的函数值,则;
D.将十进制数77转化为八进制数为116(8);
10. 如图所示给出的是计算 的值的一个程序框图,其中判断框内可以填的条件是( B )
A. B. C. D.
[来源:21世纪教育网]
二、填空题(本大题共5小题,每小题3分,共15分.)11. 如图所示的程序运行后,输出的a,b,c的值分别为_ -5,9,-5 ;
12. 按如图所示的程序框图运算,若输出的值为2,则输入的取值范围是 (28,82] ;21世纪教育网
13. 函数的值域为_ [0,1) __;
14.已知在6个电子原件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将两个次品全部找出的概率是;
15.地震的震级R与地震释放的能量E的关系为. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的倍;
三、解答题(本大题共6小题,共55分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分8分)
(1)计算:;
(2)求的定义域;
解:(1)原式=
==;
(2)由题意,得,即,
故所求定义域为,且
17.(本小题满分8分)
已知集合,,
(1)若时,求实数的取值范围;
(2)若时,求实数的取值范围;
解:
(1)由得:
则,解得,所以;
(2)当或,即或时,,
所以当时,,所以;
18.(本小题满分9分)
如图是某出租车在A、B两地间进行的一次业务活动中,离开A地的时间与相距A地的路程的函数图象. 其中纵轴s(km)表示该出租车与A地的距离,t(h)表示该出租车离开A地的时间.
(1)写出s与t的函数关系式;
(2)写出速度v(km/h)与时间t(h)的函数关系式;
(3)描述该出租车的行驶情况;
21世纪教育网[来源:21世纪教育网]
解:(1)由题图可知,该出租车从A地到B地,用2.5小时匀速行驶了150km,可求得速度为(km/h),出租车从B地回到A地,用3小时匀速行驶了150km,此时的速度为(km/h),,故s与t的函数关系式为
;
(2)车速v与时间t之间的函数关系是;
(3)该出租车的行驶情况是:先以60km/h的速度从A地驶向150km远处的B地,达到B地后停留1小时,再以50km/h的速度返回A地;
19.(本小题满分9分)
己知是定义在R上的奇函数,当时,(其中且)
(1)求函数的解析式;21世纪教育网
(2)当为何值时,的值的小于0?
解:(1)因为是定义在R上的奇函数,
当时,,所以,
(2)要使的值的小于0,则
(i)当时,或,解得,即;
(ii)当时,或,解得,即;
20.(本小题满分10分)
某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自独立进行为期一个月的技术攻关,同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为,被乙小组攻克的概率为,
(1)设为攻关期满时获奖的攻关小组数,求的分布列及数学期望;
(2)设为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数在定义域内单调递增”为事件C,求事件C发生的概率;
解:记“甲攻关小组获奖”为事件A,则P(A)= ,记“乙攻关小组获奖”为事件B,则P(B)= .
(1)由题意,的所有可能取值为0,1,2.
0 1 2
P 21世纪教育网
,
,
,所以的分布列为(见表):
(2)因为获奖攻关小组数的可能取值为0,1,2,相对应的没有获奖攻关小组数的取值为2,1,0.所以的可能取值为0,4.
当时,函数在定义域内单调递减;
当时,函数在定义域内单调递增;
所以,=+=;
21.(本小题满分11分)
已知函数,
(1)求函数的定义域;
(2)设,若函数在(2,3)内有且仅有一个零点,求实数的取值范围;
(3)设,求函数在[3,9]内的值域;
解:(1)由得,,故所求函数的定义域为{};
(2)因为在(2,3)内有且仅有一个零点,所以·,即·,得;
(3)易求得,在[3,9]内,,所以
可见取最小值的条件是,解得,此时,故存在实数,使得函数在[3,9]内的最小值为4;而,,故函数在[3,9]内的值域为;
开始
结束
输入x
是
否
输出x, k
第12题
第10题
否
结束
输出S
开始
S=0,n=2,i=1
是
i=i+1
n=n+2
a=7
b= -5
c=9
a=b
b=c
c=a
PRINT a,b,c
END
(第11题)
150
S(km)
O
2.5
3.5
6.5
t(h)
开始
结束
输入x
是
否
输出x, k
第12题
第10题
否
结束
输出S
开始
S=0,n=2,i=1
是
i=i+1
n=n+2
a=7
b= -5
c=9
a=b
b=c
c=a
PRINT a,b,c
END
(第11题)
150
S(km)
O
2.5
3.5
6.5
t(h)
数 学(理科)
命题:仇武君 审题:钟小霖
本试题卷共三大题21小题,全卷满分100分,考试时量120分钟.请将答案写在答卷上.
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.满足条件{1}={1,2}的集合M的个数是( )
A.1; B.2; C.3; D.4;
2.设集合,满足,则实数的取值范围是( )
A. ; B. ; C. ; D. ;
3.下列四个函数中,在区间上为增函数的是( )
A. ; B. ; C. ; D. ;
4.函数且的图象必经过点( )
A.(0,1); B.(1,1); C.(0,2); D.(2,0);
5.已知,,,,则( )
. . . .
6.若(其中且),则函数与的图象( )
.关于直线对称; .关于轴对称;
.关于轴对称; .关于原点对称;
7.已知函数,则( )
A.; B. ; C. ; D. ;
8.函数恰有三个零点,则的值为( )
A.0 B.2 C.4 D. 不存在
9.下列四种说法中错误的一项是( )
A.算法共有三种逻辑结构:顺序结构、条件结构、循环结构;
B.执行框除了具有赋值功能外,还具有计算功能;
C.用秦九韶算法求函数当时的函数值,则;
D.将十进制数77转化为八进制数为116(8);
10. 如图所示给出的是计算 的值的一个程序框图,其中判断框内可以填的条件是( )
A. B. C. D.
21世纪教育网
21世纪教育网
二、填空题(本大题共5小题,每小题3分,共15分.)11. 如图所示的程序运行后,输出的a,b,c的值分别为_ __;
12. 按如图所示的程序框图运算,若输出的值为2,则输入的取值范围是 ;
13. 函数的值域为_ __;
14.已知在6个电子原件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将两个次品全部找出的概率是 ;
15.地震的震级R与地震释放的能量E的关系为. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;
三、解答题(本大题共6小题,共55分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分8分)
(1)计算:;
(2)求的定义域;
17.(本小题满分8分)
已知集合,,
(1)若时,求实数的取值范围;
(2)若时,求实数的取值范围;
18.(本小题满分9分)
如图是某出租车在A、B两地间进行的一次业务活动中,离开A地的时间与相距A地的路程的函数图象. 其中纵轴s(km)表示该出租车与A地的距离,t(h)表示该出租车离开A地的时间.
(1)写出s与t的函数关系式;
(2)写出速度v(km/h)与时间t(h)的函数关系式;
(3)描述该出租车的行驶情况;
19.(本小题满分9分)
己知是定义在R上的奇函数,当时,(其中且)
(1)求函数的解析式;
(2)当为何值时,的值的小于0?
[来源:21世纪教育网]
20.(本小题满分10分)
某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自独立进行为期一个月的技术攻关,同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为,被乙小组攻克的概率为,
(1)设为攻关期满时获奖的攻关小组数,求的分布列及数学期望;
(2)设为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数在定义域内单调递增”为事件C,求事件C发生的概率;
21.(本小题满分11分)
已知函数,
(1)求函数的定义域;
(2)设,若函数在(2,3)内有且仅有一个零点,求实数的取值范围;
(3)设,求函数在[3,9]内的值域;
衡阳市八中高二学业水平模拟考试(2012.04.)
数 学(理科)(参考答案)
本试题卷共三大题21小题,全卷满分100分,考试时量120分钟.请将答案写在答卷上.[来源:21世纪教育网]
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.满足条件{1}={1,2}的集合M的个数是( B )
A.1; B.2; C.3; D.4;
2.设集合,满足,则实数的取值范围是(C)
A. ; B. ; C. ; D. ;
3.下列四个函数中,在区间上为增函数的是(C )
A. ; B. ; C. ; D. ;
4.函数且的图象必经过点(C)
A.(0,1); B.(1,1); C.(0,2); D.(2,0);
5.已知,,,,则(D)
. . . .
6.若(其中且),则函数与的图象(C)
.关于直线对称; .关于轴对称;
.关于轴对称; .关于原点对称;
7.已知函数,则(A)
A.; B. ; C. ; D. ;
8.函数恰有三个零点,则的值为( C)
A.0 B.2 C.4 D. 不存在
9.下列四种说法中错误的一项是( D)
A.算法共有三种逻辑结构:顺序结构、条件结构、循环结构;
B.执行框除了具有赋值功能外,还具有计算功能;
C.用秦九韶算法求函数当时的函数值,则;
D.将十进制数77转化为八进制数为116(8);
10. 如图所示给出的是计算 的值的一个程序框图,其中判断框内可以填的条件是( B )
A. B. C. D.
[来源:21世纪教育网]
二、填空题(本大题共5小题,每小题3分,共15分.)11. 如图所示的程序运行后,输出的a,b,c的值分别为_ -5,9,-5 ;
12. 按如图所示的程序框图运算,若输出的值为2,则输入的取值范围是 (28,82] ;21世纪教育网
13. 函数的值域为_ [0,1) __;
14.已知在6个电子原件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将两个次品全部找出的概率是;
15.地震的震级R与地震释放的能量E的关系为. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的倍;
三、解答题(本大题共6小题,共55分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分8分)
(1)计算:;
(2)求的定义域;
解:(1)原式=
==;
(2)由题意,得,即,
故所求定义域为,且
17.(本小题满分8分)
已知集合,,
(1)若时,求实数的取值范围;
(2)若时,求实数的取值范围;
解:
(1)由得:
则,解得,所以;
(2)当或,即或时,,
所以当时,,所以;
18.(本小题满分9分)
如图是某出租车在A、B两地间进行的一次业务活动中,离开A地的时间与相距A地的路程的函数图象. 其中纵轴s(km)表示该出租车与A地的距离,t(h)表示该出租车离开A地的时间.
(1)写出s与t的函数关系式;
(2)写出速度v(km/h)与时间t(h)的函数关系式;
(3)描述该出租车的行驶情况;
21世纪教育网[来源:21世纪教育网]
解:(1)由题图可知,该出租车从A地到B地,用2.5小时匀速行驶了150km,可求得速度为(km/h),出租车从B地回到A地,用3小时匀速行驶了150km,此时的速度为(km/h),,故s与t的函数关系式为
;
(2)车速v与时间t之间的函数关系是;
(3)该出租车的行驶情况是:先以60km/h的速度从A地驶向150km远处的B地,达到B地后停留1小时,再以50km/h的速度返回A地;
19.(本小题满分9分)
己知是定义在R上的奇函数,当时,(其中且)
(1)求函数的解析式;21世纪教育网
(2)当为何值时,的值的小于0?
解:(1)因为是定义在R上的奇函数,
当时,,所以,
(2)要使的值的小于0,则
(i)当时,或,解得,即;
(ii)当时,或,解得,即;
20.(本小题满分10分)
某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自独立进行为期一个月的技术攻关,同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为,被乙小组攻克的概率为,
(1)设为攻关期满时获奖的攻关小组数,求的分布列及数学期望;
(2)设为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数在定义域内单调递增”为事件C,求事件C发生的概率;
解:记“甲攻关小组获奖”为事件A,则P(A)= ,记“乙攻关小组获奖”为事件B,则P(B)= .
(1)由题意,的所有可能取值为0,1,2.
0 1 2
P 21世纪教育网
,
,
,所以的分布列为(见表):
(2)因为获奖攻关小组数的可能取值为0,1,2,相对应的没有获奖攻关小组数的取值为2,1,0.所以的可能取值为0,4.
当时,函数在定义域内单调递减;
当时,函数在定义域内单调递增;
所以,=+=;
21.(本小题满分11分)
已知函数,
(1)求函数的定义域;
(2)设,若函数在(2,3)内有且仅有一个零点,求实数的取值范围;
(3)设,求函数在[3,9]内的值域;
解:(1)由得,,故所求函数的定义域为{};
(2)因为在(2,3)内有且仅有一个零点,所以·,即·,得;
(3)易求得,在[3,9]内,,所以
可见取最小值的条件是,解得,此时,故存在实数,使得函数在[3,9]内的最小值为4;而,,故函数在[3,9]内的值域为;
开始
结束
输入x
是
否
输出x, k
第12题
第10题
否
结束
输出S
开始
S=0,n=2,i=1
是
i=i+1
n=n+2
a=7
b= -5
c=9
a=b
b=c
c=a
PRINT a,b,c
END
(第11题)
150
S(km)
O
2.5
3.5
6.5
t(h)
开始
结束
输入x
是
否
输出x, k
第12题
第10题
否
结束
输出S
开始
S=0,n=2,i=1
是
i=i+1
n=n+2
a=7
b= -5
c=9
a=b
b=c
c=a
PRINT a,b,c
END
(第11题)
150
S(km)
O
2.5
3.5
6.5
t(h)
同课章节目录
