2012年中考专题复习第1课时阅读理解题
文档属性
| 名称 | 2012年中考专题复习第1课时阅读理解题 |  | |
| 格式 | zip | ||
| 文件大小 | 309.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-09 16:33:28 | ||
图片预览




文档简介
第1课时 阅读理解题
所谓数学的阅读理解题,就是题目首先提供一定的材料,或介绍一个概念,或给出一种解法等,让你在理解材料的基础上,获得探索解决问题的方法,从而加以运用,解决实际问题.其目的在于考查学生的阅读理解能力、收集处理信息的能力和运用知识解决实际问题的能力.
阅读理解题的篇幅一般都较长,试题结构大致分两部分:一部分是阅读材料,别一部分是根据阅读材料需解决的有关问题.阅读材料既有选用与教材知识相关的内容的,也有广泛选用课外知识的.考查目标除了初中数学和基础知识外,更注重考查阅读理解、分析转化、范例运用、探索归纳等多方面的素质和能力.因此,这类问题需要学生通过对阅读材料的阅读理解,然后进行合情推理,就其本质进行归纳加工、猜想、类比和联想,作出合情判断和推理.
解决型阅读题的关键是首先仔细阅读信息,弄清信息所提供的数量关系,然后将信息转化为数学问题,感悟数学思想和方法,形成科学的思维方式和思维策略,进而解决问题.
类型一 模仿型阅读理解题
在已有知识的基础上,设计一个陌生的数学情景,通过阅读相关信息,根据题目引入新知识进行猜想解答的一类新题型.解题关键是理解材料中所提供的解题途径和方法,运用归纳与类比的方法 去探索新的解题方法.问题解答并不太难,虽出发点低,但落脚点高.是“学生的可持续发展”理念的体现。
例1、(2011年贵阳)[阅读]在平面直角坐标系中,以任意两点、为端点的线段中点坐标为.
[运用](1)如图,矩形的对角线相交于点,、在轴和轴上,坐标原点,点的坐标为,则点的坐标为 ;
(2)在直角坐标系中,有,,三点,另有一点与、、构成平行四边形的顶点,求点的坐标.
例2、(2011年衢州)某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?
小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为元,由题意
得 化简,整理得:
解这个方程,得:,,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系:
__________________________________________________________________
(2)请用一种与小明不相同的方法求解上述问题。
类型二 考查掌握新知识能力的阅读理解题
命题者给定一个陌生的定义或公式或方法,让你去解决新问题,这类考题能考查解题者自学能力和阅读理解能力,能考查解题者接收、加工和利用信息的能力。 ( http: / / www.21cnjy.com / )
例3、(2011年浙江)定义新运算“”如下:当时. ,当时.;若,则_________。
例4、(2011年宁波)阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
① 求证:△ACE是奇异三角形;
② 当△ACE是直角三角形时,求∠AOC的度数.
类型之三 操作型阅读理解题
操作型阅读理解题通常先提供图形变化的方法步骤.解题的时候,你只要根据题目所提供的操作步骤一步步解题即可.它能有效检测学生的创新意识和创新能力的好题型,是中考改革的必然产物.这类问题能较好地考查学生用数学的能力,具有很强的开放性并具有一定的趣味性和挑战性.
例5、(2010台州)一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
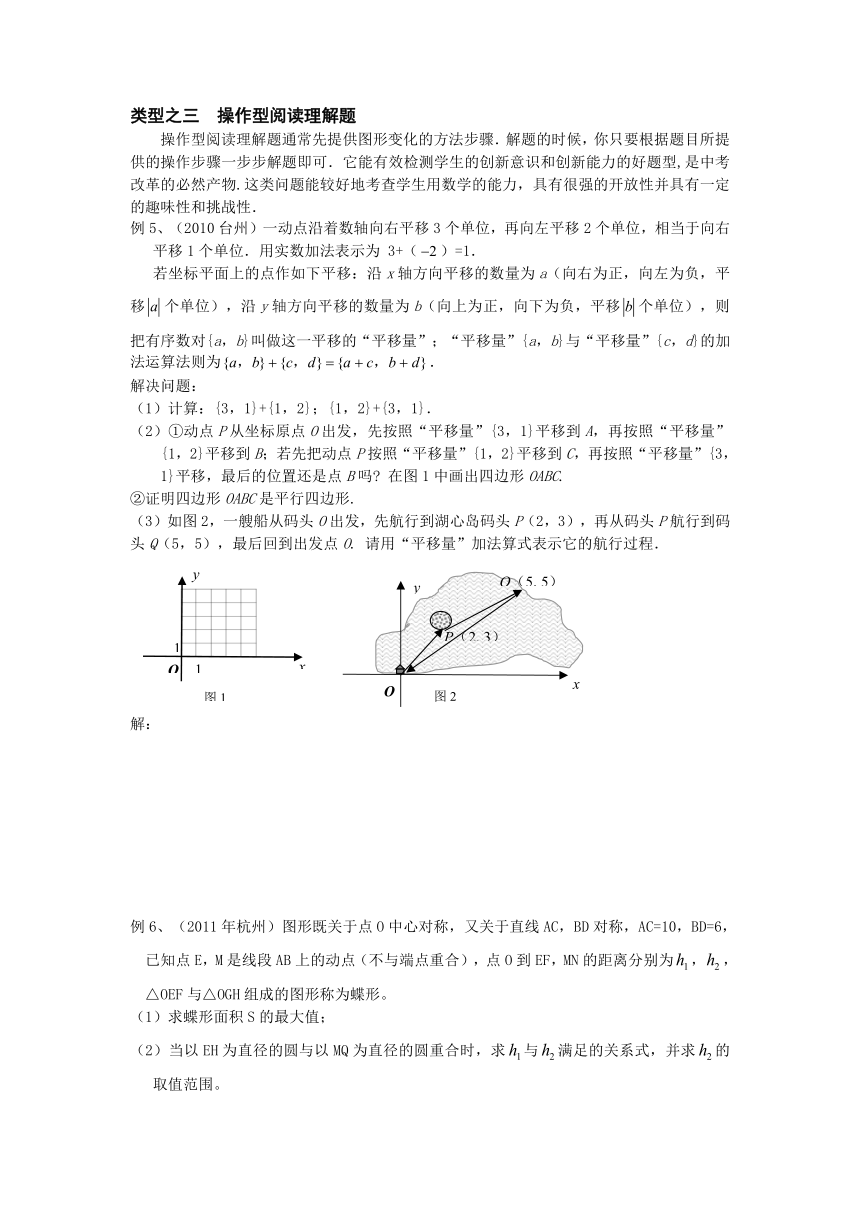
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
解:
例6、(2011年杭州)图形既关于点O中心对称,又关于直线AC,BD对称,AC=10,BD=6,已知点E,M是线段AB上的动点(不与端点重合),点O到EF,MN的距离分别为,,△OEF与△OGH组成的图形称为蝶形。
(1)求蝶形面积S的最大值;
(2)当以EH为直径的圆与以MQ为直径的圆重合时,求与满足的关系式,并求的取值范围。
例7、阅读理解:对于任意正实数a、b,∵≥0, ∴≥0,
∴ ≥,只有当a=b时,等号成立.
结论:在≥(a、b均为正实数)中,若ab为定值p,则a+b≥,
只有当a=b时,a+b有最小值.
根据上述内容,回答下列问题:
若m>0,只有当m= 时,有最小值 .
思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.
试根据图形验证≥,并指出等号成立时的条件.
探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
课后练习
1、让我们轻松一下,做一个数字游戏:
第一步:取一个自然数n1=5 ,计算n12+1得a1; ( http: / / www.21cnjy.com / )
第二步:算出a1的各位数字之和得n2,计算n22+1得a2;
第三步:算出a2的各位数字之和得n3,再计算n23+1得a3; ( http: / / www.21cnjy.com / )…………
依此类推,则a=____________.
2、用“”与“”表示一种法则:(ab)= -b,(ab)= -a,如(23)= -3,则 .
3、(珠海)我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2, (1011)2换算成十进制数应为:
按此方式,将二进制(1001)2换算成十进制数的结果是_______________.
4、符号“”称为二阶行列式,规定它的运算法则为:,请你根据上述规定求出等式中的值.
解:
5、阅读材料,解答下列问题. ( http: / / www.21cnjy.com / )
例:当时,如则,故此时的绝对值是它本身
当时,,故此时的绝对值是零
当时,如则,故此时的绝对值是它的相反数;
综合起来一个数的绝对值要分三种情况,即
这种分析方法涌透了数学的分类讨论思想. ( http: / / www.21cnjy.com / )
问:(1)请仿照例中的分类讨论的方法,分析二次根式的各种展开的情况.
(2)猜想与的大小关系.
解:
6、阅读下列材料,并解决后面的问题:
★ 阅读材料:(1) 等高线概念:在地图上,我们把地面上海拔高度相同的点连成的闭合曲线叫等高线。例如,如图1,把海拔高度是50米、100米、150米的点分别连接起来,就分别形成50米、100米、150米三条等高线。
(2) 利用等高线地形图求坡度的步骤如下:(如图2)
步骤一:根据两点A、B所在的等高线地形图,分别读出点A、B的高度;A、B两点的铅直距离=点A、B的高度差;
步骤二:量出AB在等高线地形图上的距离为d个单位,若等高线地形图的比例尺为 1:n,则A、B两点的水平距离=dn;
步骤三:AB的坡度==;
★请按照下列求解过程完成填空,并把所得结果直接写在答题卡上。
某中学学生小明和小丁生活在山城,如图3(示意图),小明每天上学从家A经过B沿着公路AB、BP到学校P,小丁每天上学从家C沿着公路CP到学校P。该山城等高线地形图的比例尺为1:50000,在等高线地形图上量得AB=1.8厘米,BP=3.6厘米,CP=4.2厘米。
(1)分别求出AB、BP、CP的坡度(同一段路中间坡度的微小变化忽略不计);
(2)若他们早晨7点同时步行从家出发,中途不停留,谁先到学校?(假设当坡度在到之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在到之间时,小明和小丁步行的平均速度均约为1米/秒)
7、在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=x+3的坐标三角形的三条边长;
(2)若函数y=x+b(b为常数)的坐标三角形周长为16,
求此三角形面积.
解:
8、请阅读下列材料:
问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连结PG,PC.若,探究PG与PC的位置关系及的值.
小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段PG与PC的位置关系及的值;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中,将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含的式子表示).
解:(1)线段与的位置关系是 ;HYPERLINK "http://www.21cnjy.com/" .
第1课时 阅读理解题答案
例1、解:(1)M=(,)=(2,1.5).
(2)根据平行四边形的对角线互相平分可得:D'(1,﹣1),D''(﹣3,5),D''(5,3).
点评:本题考查了平行四边形的性质及矩形的性质,比较简单,关键是掌握已知两点求其中点坐标的方法.
例2、解:(1)平均单株盈利株数=每盆盈利
平均单株盈利=每盆增加的株数 每盆的株数=3+每盆增加的株数
(2)解法1(列表法)
每盆植入株数 平均单株盈利(元) 每盆盈利(元)
3 3 9
4 2.5 10
5 2 10
6 1.5 9
7 1 7
… … …
答:要使每盆的盈利达到10元,每盆应该植入4株或5株;
解法2(图象法)
如图,纵轴表示平均单株盈利,横轴表示株数,则相应长方形面积表示每盆盈利。
从图象可知,每盆植入4株或5株时,相应长方形面积都是10
答:要使每盆的盈利达到10元,每盆应该植入4株或5株。
解法3(函数法)
解:设每盆花苗增加x,每盆的盈利为y元,根据题意得可得:
当y=10时,
解这个方程得:,
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
解法4(列分式方程)
解:设每盆花苗增加x株时,每盆盈利10元,根据题意,得:
解这个方程得:,
经检验,,都是所列方程的解
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
例4、解:(1) 真命题
(2) 在Rt△ABC中, ∵
∴, ∴若Rt△ABC为奇异三角形,一定有
∴ ∴ 得
∵ ∴ ∴
(3) ①∵AB是⊙O的直径 ∴∠ACB=∠ADB=90°
在Rt△ACB中, 在Rt△ADB中,
∵点D是半圆ADB的中点 ∴AD= BD ∴AD=BD
∴ ∴
又∵ ∴ ∴△是奇异三角形
②由①可得△是奇异三角形 ∴
当△是直角三角形时 由(2)可得或
(Ⅰ)当时, 即
∵ ∴ ∴
(Ⅱ)当时, 即
∵ ∴ ∴
∴的度数为.
例5、解:(1){3,1}+{1,2}={4,3}. {1,2}+{3,1}={4,3}.
(2)①画图 最后的位置仍是B.
② 证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB==,OA=BC==, ∴四边形OABC是平行四边形.
(3){2,3}+{3,2}+{-5,-5}={0, 0}.
例6、解:(1)由题意,得四边形是菱形.
由,得,,即
所以当时,.
(2)根据题意,得.
如图,作于, 关于对称线段为,
1)当点不重合时,则在的两侧,易知.
,
由,得
,即
,此时的取值范围为且
2)当点重合时,则,此时的取值范围为.
例7、解:阅读理解:m= 1 ,最小值为 2 ;
思考验证:∵AB是的直径, ∴AC⊥BC,又∵CD⊥AB,∴∠CAD=∠BCD=90°-∠B,
∴Rt△CAD∽Rt△BCD, CD2=AD·DB, ∴CD= 若点D与O不重合,连OC,在Rt△OCD中,∵OC>CD, ∴, 若点D与O重合时,OC=CD,∴
综上所述,,当CD等于半径时,等号成立.
探索应用:设, 则, ,
, 化简得:
, 只有当
∴S≥2×6+12=24, ∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.
课后练习
1、【解析】本题是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律。由题目得,a1=26;n2=8,a2=65;n3=11,a3=122;看不出什么规律,那就继续:n4=5,a4=26;…;这样就发现规 律:每三个为一个循环,÷3=669……1;即a= a1=26。答案为26。 【答案】26
2、【答案】2011
3. 9
4、解: 整理得:2×-=1 +=1 解之得:x=4 ( http: / / www.21cnjy.com / )
5、解:(1)写出类似例的文字描述 (2)
6、解:(1) AB的水平距离=1.850000=90000(厘米)=900(米),AB的坡度==;
BP的水平距离=3.650000=180000(厘米)=1800(米),BP的坡度==;
CP的水平距离=4.250000=210000(厘米)=2100(米),CP的坡度= ;
(2) 因为<<,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。
因为 ,所以小丁在路段CP上步行的平均速度约为 米/秒,斜坡AB的距离=906(米),斜坡BP的距离=1811(米),斜坡CP的距离=2121(米),所以小明从家到学校的时间==2090(秒)。小丁从家到学校的时间约为 秒。因此, 先到学校。
7、解:(1) ∵ 直线y=x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=x+3的坐标三角形的三条边长分别为3,4,5.
(2) 直线y=x+b与x轴的交点坐标为(,0),与y轴交点坐标为(0,b),
当b>0时,,得b =4,此时,坐标三角形面积为;
当b<0时,,得b =-4,此时,坐标三角形面积为.
综上,当函数y=x+b的坐标三角形周长为16时,面积为.
8、解:(1)线段PG与PC的位置关系是;.
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP交AD于点H,连结CH和CG. P是线段的中点, .
由题意可知. . ,
.,. 四边形是菱形,
,.
由,且菱形的对角线恰好与菱形的边在同一条直线上, 可得. .四边形是菱形,
. . . ,.
. 即.,,
,. .
(3).
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
单株盈利(元)
3
2.5
2
1.5
1
0.5
0
1
2
3
4
5
6
7
(3,3)
(4,2.5)
(5,2)
(6,1.5)
(7,1)
株数
所谓数学的阅读理解题,就是题目首先提供一定的材料,或介绍一个概念,或给出一种解法等,让你在理解材料的基础上,获得探索解决问题的方法,从而加以运用,解决实际问题.其目的在于考查学生的阅读理解能力、收集处理信息的能力和运用知识解决实际问题的能力.
阅读理解题的篇幅一般都较长,试题结构大致分两部分:一部分是阅读材料,别一部分是根据阅读材料需解决的有关问题.阅读材料既有选用与教材知识相关的内容的,也有广泛选用课外知识的.考查目标除了初中数学和基础知识外,更注重考查阅读理解、分析转化、范例运用、探索归纳等多方面的素质和能力.因此,这类问题需要学生通过对阅读材料的阅读理解,然后进行合情推理,就其本质进行归纳加工、猜想、类比和联想,作出合情判断和推理.
解决型阅读题的关键是首先仔细阅读信息,弄清信息所提供的数量关系,然后将信息转化为数学问题,感悟数学思想和方法,形成科学的思维方式和思维策略,进而解决问题.
类型一 模仿型阅读理解题
在已有知识的基础上,设计一个陌生的数学情景,通过阅读相关信息,根据题目引入新知识进行猜想解答的一类新题型.解题关键是理解材料中所提供的解题途径和方法,运用归纳与类比的方法 去探索新的解题方法.问题解答并不太难,虽出发点低,但落脚点高.是“学生的可持续发展”理念的体现。
例1、(2011年贵阳)[阅读]在平面直角坐标系中,以任意两点、为端点的线段中点坐标为.
[运用](1)如图,矩形的对角线相交于点,、在轴和轴上,坐标原点,点的坐标为,则点的坐标为 ;
(2)在直角坐标系中,有,,三点,另有一点与、、构成平行四边形的顶点,求点的坐标.
例2、(2011年衢州)某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?
小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为元,由题意
得 化简,整理得:
解这个方程,得:,,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系:
__________________________________________________________________
(2)请用一种与小明不相同的方法求解上述问题。
类型二 考查掌握新知识能力的阅读理解题
命题者给定一个陌生的定义或公式或方法,让你去解决新问题,这类考题能考查解题者自学能力和阅读理解能力,能考查解题者接收、加工和利用信息的能力。 ( http: / / www.21cnjy.com / )
例3、(2011年浙江)定义新运算“”如下:当时. ,当时.;若,则_________。
例4、(2011年宁波)阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
① 求证:△ACE是奇异三角形;
② 当△ACE是直角三角形时,求∠AOC的度数.
类型之三 操作型阅读理解题
操作型阅读理解题通常先提供图形变化的方法步骤.解题的时候,你只要根据题目所提供的操作步骤一步步解题即可.它能有效检测学生的创新意识和创新能力的好题型,是中考改革的必然产物.这类问题能较好地考查学生用数学的能力,具有很强的开放性并具有一定的趣味性和挑战性.
例5、(2010台州)一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
解:
例6、(2011年杭州)图形既关于点O中心对称,又关于直线AC,BD对称,AC=10,BD=6,已知点E,M是线段AB上的动点(不与端点重合),点O到EF,MN的距离分别为,,△OEF与△OGH组成的图形称为蝶形。
(1)求蝶形面积S的最大值;
(2)当以EH为直径的圆与以MQ为直径的圆重合时,求与满足的关系式,并求的取值范围。
例7、阅读理解:对于任意正实数a、b,∵≥0, ∴≥0,
∴ ≥,只有当a=b时,等号成立.
结论:在≥(a、b均为正实数)中,若ab为定值p,则a+b≥,
只有当a=b时,a+b有最小值.
根据上述内容,回答下列问题:
若m>0,只有当m= 时,有最小值 .
思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.
试根据图形验证≥,并指出等号成立时的条件.
探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
课后练习
1、让我们轻松一下,做一个数字游戏:
第一步:取一个自然数n1=5 ,计算n12+1得a1; ( http: / / www.21cnjy.com / )
第二步:算出a1的各位数字之和得n2,计算n22+1得a2;
第三步:算出a2的各位数字之和得n3,再计算n23+1得a3; ( http: / / www.21cnjy.com / )…………
依此类推,则a=____________.
2、用“”与“”表示一种法则:(ab)= -b,(ab)= -a,如(23)= -3,则 .
3、(珠海)我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2, (1011)2换算成十进制数应为:
按此方式,将二进制(1001)2换算成十进制数的结果是_______________.
4、符号“”称为二阶行列式,规定它的运算法则为:,请你根据上述规定求出等式中的值.
解:
5、阅读材料,解答下列问题. ( http: / / www.21cnjy.com / )
例:当时,如则,故此时的绝对值是它本身
当时,,故此时的绝对值是零
当时,如则,故此时的绝对值是它的相反数;
综合起来一个数的绝对值要分三种情况,即
这种分析方法涌透了数学的分类讨论思想. ( http: / / www.21cnjy.com / )
问:(1)请仿照例中的分类讨论的方法,分析二次根式的各种展开的情况.
(2)猜想与的大小关系.
解:
6、阅读下列材料,并解决后面的问题:
★ 阅读材料:(1) 等高线概念:在地图上,我们把地面上海拔高度相同的点连成的闭合曲线叫等高线。例如,如图1,把海拔高度是50米、100米、150米的点分别连接起来,就分别形成50米、100米、150米三条等高线。
(2) 利用等高线地形图求坡度的步骤如下:(如图2)
步骤一:根据两点A、B所在的等高线地形图,分别读出点A、B的高度;A、B两点的铅直距离=点A、B的高度差;
步骤二:量出AB在等高线地形图上的距离为d个单位,若等高线地形图的比例尺为 1:n,则A、B两点的水平距离=dn;
步骤三:AB的坡度==;
★请按照下列求解过程完成填空,并把所得结果直接写在答题卡上。
某中学学生小明和小丁生活在山城,如图3(示意图),小明每天上学从家A经过B沿着公路AB、BP到学校P,小丁每天上学从家C沿着公路CP到学校P。该山城等高线地形图的比例尺为1:50000,在等高线地形图上量得AB=1.8厘米,BP=3.6厘米,CP=4.2厘米。
(1)分别求出AB、BP、CP的坡度(同一段路中间坡度的微小变化忽略不计);
(2)若他们早晨7点同时步行从家出发,中途不停留,谁先到学校?(假设当坡度在到之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在到之间时,小明和小丁步行的平均速度均约为1米/秒)
7、在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=x+3的坐标三角形的三条边长;
(2)若函数y=x+b(b为常数)的坐标三角形周长为16,
求此三角形面积.
解:
8、请阅读下列材料:
问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连结PG,PC.若,探究PG与PC的位置关系及的值.
小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段PG与PC的位置关系及的值;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中,将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含的式子表示).
解:(1)线段与的位置关系是 ;HYPERLINK "http://www.21cnjy.com/" .
第1课时 阅读理解题答案
例1、解:(1)M=(,)=(2,1.5).
(2)根据平行四边形的对角线互相平分可得:D'(1,﹣1),D''(﹣3,5),D''(5,3).
点评:本题考查了平行四边形的性质及矩形的性质,比较简单,关键是掌握已知两点求其中点坐标的方法.
例2、解:(1)平均单株盈利株数=每盆盈利
平均单株盈利=每盆增加的株数 每盆的株数=3+每盆增加的株数
(2)解法1(列表法)
每盆植入株数 平均单株盈利(元) 每盆盈利(元)
3 3 9
4 2.5 10
5 2 10
6 1.5 9
7 1 7
… … …
答:要使每盆的盈利达到10元,每盆应该植入4株或5株;
解法2(图象法)
如图,纵轴表示平均单株盈利,横轴表示株数,则相应长方形面积表示每盆盈利。
从图象可知,每盆植入4株或5株时,相应长方形面积都是10
答:要使每盆的盈利达到10元,每盆应该植入4株或5株。
解法3(函数法)
解:设每盆花苗增加x,每盆的盈利为y元,根据题意得可得:
当y=10时,
解这个方程得:,
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
解法4(列分式方程)
解:设每盆花苗增加x株时,每盆盈利10元,根据题意,得:
解这个方程得:,
经检验,,都是所列方程的解
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
例4、解:(1) 真命题
(2) 在Rt△ABC中, ∵
∴, ∴若Rt△ABC为奇异三角形,一定有
∴ ∴ 得
∵ ∴ ∴
(3) ①∵AB是⊙O的直径 ∴∠ACB=∠ADB=90°
在Rt△ACB中, 在Rt△ADB中,
∵点D是半圆ADB的中点 ∴AD= BD ∴AD=BD
∴ ∴
又∵ ∴ ∴△是奇异三角形
②由①可得△是奇异三角形 ∴
当△是直角三角形时 由(2)可得或
(Ⅰ)当时, 即
∵ ∴ ∴
(Ⅱ)当时, 即
∵ ∴ ∴
∴的度数为.
例5、解:(1){3,1}+{1,2}={4,3}. {1,2}+{3,1}={4,3}.
(2)①画图 最后的位置仍是B.
② 证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB==,OA=BC==, ∴四边形OABC是平行四边形.
(3){2,3}+{3,2}+{-5,-5}={0, 0}.
例6、解:(1)由题意,得四边形是菱形.
由,得,,即
所以当时,.
(2)根据题意,得.
如图,作于, 关于对称线段为,
1)当点不重合时,则在的两侧,易知.
,
由,得
,即
,此时的取值范围为且
2)当点重合时,则,此时的取值范围为.
例7、解:阅读理解:m= 1 ,最小值为 2 ;
思考验证:∵AB是的直径, ∴AC⊥BC,又∵CD⊥AB,∴∠CAD=∠BCD=90°-∠B,
∴Rt△CAD∽Rt△BCD, CD2=AD·DB, ∴CD= 若点D与O不重合,连OC,在Rt△OCD中,∵OC>CD, ∴, 若点D与O重合时,OC=CD,∴
综上所述,,当CD等于半径时,等号成立.
探索应用:设, 则, ,
, 化简得:
, 只有当
∴S≥2×6+12=24, ∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.
课后练习
1、【解析】本题是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律。由题目得,a1=26;n2=8,a2=65;n3=11,a3=122;看不出什么规律,那就继续:n4=5,a4=26;…;这样就发现规 律:每三个为一个循环,÷3=669……1;即a= a1=26。答案为26。 【答案】26
2、【答案】2011
3. 9
4、解: 整理得:2×-=1 +=1 解之得:x=4 ( http: / / www.21cnjy.com / )
5、解:(1)写出类似例的文字描述 (2)
6、解:(1) AB的水平距离=1.850000=90000(厘米)=900(米),AB的坡度==;
BP的水平距离=3.650000=180000(厘米)=1800(米),BP的坡度==;
CP的水平距离=4.250000=210000(厘米)=2100(米),CP的坡度= ;
(2) 因为<<,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。
因为 ,所以小丁在路段CP上步行的平均速度约为 米/秒,斜坡AB的距离=906(米),斜坡BP的距离=1811(米),斜坡CP的距离=2121(米),所以小明从家到学校的时间==2090(秒)。小丁从家到学校的时间约为 秒。因此, 先到学校。
7、解:(1) ∵ 直线y=x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=x+3的坐标三角形的三条边长分别为3,4,5.
(2) 直线y=x+b与x轴的交点坐标为(,0),与y轴交点坐标为(0,b),
当b>0时,,得b =4,此时,坐标三角形面积为;
当b<0时,,得b =-4,此时,坐标三角形面积为.
综上,当函数y=x+b的坐标三角形周长为16时,面积为.
8、解:(1)线段PG与PC的位置关系是;.
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP交AD于点H,连结CH和CG. P是线段的中点, .
由题意可知. . ,
.,. 四边形是菱形,
,.
由,且菱形的对角线恰好与菱形的边在同一条直线上, 可得. .四边形是菱形,
. . . ,.
. 即.,,
,. .
(3).
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
单株盈利(元)
3
2.5
2
1.5
1
0.5
0
1
2
3
4
5
6
7
(3,3)
(4,2.5)
(5,2)
(6,1.5)
(7,1)
株数
同课章节目录
