7.5正态分布 学案-2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.5正态分布 学案-2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 21:18:17 | ||
图片预览


文档简介
高中数学人教A版(2019)选择性必修第三册7.5正态分布
学案
一、学习目标
1.
通过具体实例,了解服从正态分布的随机变量,借助频率分布直方图的几何直观,了解正态分布的特征;
2.
能够根据正态曲线的特点求随机变量在某一区间内的概率;
3.
了解正态分布的均值、方差及其含义,会用正态分布解决实际问题.
二、基础梳理
1.
对任意的,,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称为_____________,称它的图象为_____________,简称_____________.若随机变量X的概率分布密度函数为,则称随机变量X服从_____________,记为.特别地,当时,称随机变量X服从_____________.
2.
正态曲线的特点:
(1)曲线是单峰的,它关于直线__________对称;
(2)曲线在__________处达到峰值__________;
(3)当无限增大时,曲线无限接近__________轴.
3.
参数反映了正态分布的集中位置,反映了随机变量的分布相对于均值的离散程度.若,则.
三、巩固练习
1.已知随机变量X服从正态分布,且,则实数a的值为(
)
A.1
B.
C.2
D.4
2.随机变量服从正态分布,则(
)
A.0.7
B.0.4
C.0.2
D.0.15
3.某中学在高三上学期期末考试中,理科学生的数学成绩.若已知,则从该校理科生中任选一名学生,他的数学成绩大于120分的概率为(
)
A.0.86
B.0.64
C.0.36
D.0.14
4.已知随机变量,且,则(
)
A.
B.
C.
D.
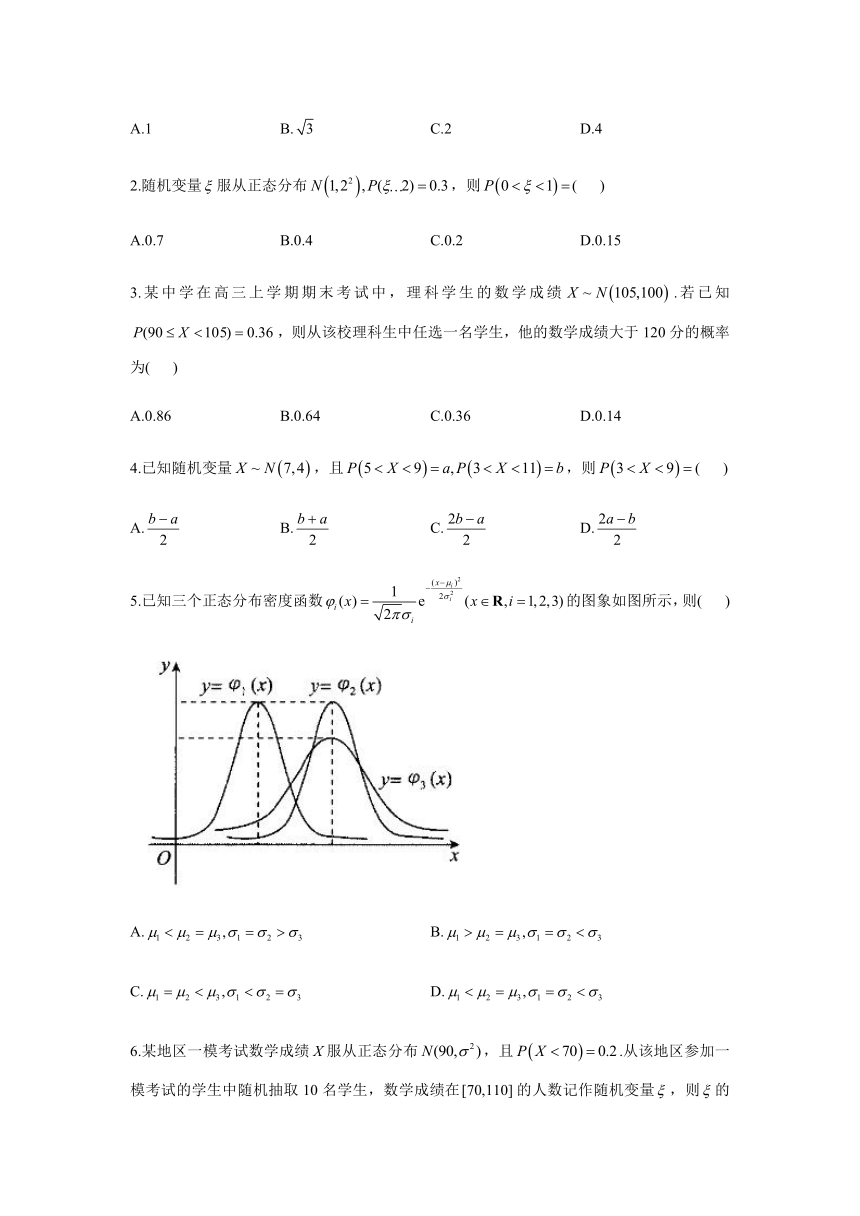
5.已知三个正态分布密度函数的图象如图所示,则(
)
A.
B.
C.
D.
6.某地区一模考试数学成绩X服从正态分布,且.从该地区参加一模考试的学生中随机抽取10名学生,数学成绩在的人数记作随机变量,则的方差为(
)
A.2
B.2.1
C.2.4
D.3
7.在一次共有10000名考生的某市高二的联考中,这些学生的数学成绩服从正态分布,且.若按成绩分层随机抽样的方式抽取100份试卷进行分析,应从120分以上的试卷中抽取(
)
A.20份
B.15份
C.10份
D.5份
8.设随机变量X服从正态分布,若,则实数_____.
9.已知随机变量X服从正态分布,若,则______.
10.某制造企业向A高校3D打印实验团队租用一台3D打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10个零件,测量其内径的数据如下(单位:).
97
97
98
102
105
107
108
109
113
114
(1)计算平均值与标准差.
(2)假设这台3D打印设备打印出的零件内径Z服从正态分布,该团队到工厂安装调试后,试打了5个零件,度量其内径分别为(单位:)86,95,103,109,118,试问此打印设备是否需要进一步调试,为什么?
参考数据:,
.
参考答案
基础梳理
正态密度曲线;正态密度曲线;正态曲线;正态分布;;标准正态分布
;;;x;;
巩固练习
1.答案:A
解析:随机变量X服从正态分布,
.由,可知.
2.答案:C
解析:由题意,随机变量服从正态分布,
∴正态曲线的对称轴是直线.
又,
,故选
C.
3.答案:D
解析:因为学生成绩X服从正态分布,所以.
因为,所以,
所以,故选D.
4.答案:B
解析:由正态曲线的对称性知,故选B.
5.答案:D
解析:正态分布密度函数为,则对应函数图象的对称轴为直线.
正态曲线关于直线对称,.
越小曲线越“瘦高”,
函数中的比函数中的要小,函数和的值相等.故选D.
6.答案:C
解析:由正态分布知,每个人数学成绩在的概率为,
所以10个学生数学成绩在的人数服从二项分布,
所以方差为,故选C.
7.答案:C
解析:由题意,数学成绩服从正态分布,且根据正态分布密度曲线的对称性,可得所以0.8)=0.1.所以按成绩分层随机抽样抽取100份试卷时,应从120分以上的试卷中抽取份,故选C.
8.答案:
解析:因为随机变量X服从正态分布且所以由正态曲线的对称性可知解得.
9.答案:0.954
解析:∵随机变量X服从正态分布,
∴正态分布密度曲线关于直线对称.
.
.
10.答案:(1)利用测量数据,即可计算平均值与标准差.
.
.
(2)需要进一步调试.服从正态分布,
,
∴内径在之外的概率为0.003,而,根据原则,需要进一步调试.
学案
一、学习目标
1.
通过具体实例,了解服从正态分布的随机变量,借助频率分布直方图的几何直观,了解正态分布的特征;
2.
能够根据正态曲线的特点求随机变量在某一区间内的概率;
3.
了解正态分布的均值、方差及其含义,会用正态分布解决实际问题.
二、基础梳理
1.
对任意的,,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称为_____________,称它的图象为_____________,简称_____________.若随机变量X的概率分布密度函数为,则称随机变量X服从_____________,记为.特别地,当时,称随机变量X服从_____________.
2.
正态曲线的特点:
(1)曲线是单峰的,它关于直线__________对称;
(2)曲线在__________处达到峰值__________;
(3)当无限增大时,曲线无限接近__________轴.
3.
参数反映了正态分布的集中位置,反映了随机变量的分布相对于均值的离散程度.若,则.
三、巩固练习
1.已知随机变量X服从正态分布,且,则实数a的值为(
)
A.1
B.
C.2
D.4
2.随机变量服从正态分布,则(
)
A.0.7
B.0.4
C.0.2
D.0.15
3.某中学在高三上学期期末考试中,理科学生的数学成绩.若已知,则从该校理科生中任选一名学生,他的数学成绩大于120分的概率为(
)
A.0.86
B.0.64
C.0.36
D.0.14
4.已知随机变量,且,则(
)
A.
B.
C.
D.
5.已知三个正态分布密度函数的图象如图所示,则(
)
A.
B.
C.
D.
6.某地区一模考试数学成绩X服从正态分布,且.从该地区参加一模考试的学生中随机抽取10名学生,数学成绩在的人数记作随机变量,则的方差为(
)
A.2
B.2.1
C.2.4
D.3
7.在一次共有10000名考生的某市高二的联考中,这些学生的数学成绩服从正态分布,且.若按成绩分层随机抽样的方式抽取100份试卷进行分析,应从120分以上的试卷中抽取(
)
A.20份
B.15份
C.10份
D.5份
8.设随机变量X服从正态分布,若,则实数_____.
9.已知随机变量X服从正态分布,若,则______.
10.某制造企业向A高校3D打印实验团队租用一台3D打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10个零件,测量其内径的数据如下(单位:).
97
97
98
102
105
107
108
109
113
114
(1)计算平均值与标准差.
(2)假设这台3D打印设备打印出的零件内径Z服从正态分布,该团队到工厂安装调试后,试打了5个零件,度量其内径分别为(单位:)86,95,103,109,118,试问此打印设备是否需要进一步调试,为什么?
参考数据:,
.
参考答案
基础梳理
正态密度曲线;正态密度曲线;正态曲线;正态分布;;标准正态分布
;;;x;;
巩固练习
1.答案:A
解析:随机变量X服从正态分布,
.由,可知.
2.答案:C
解析:由题意,随机变量服从正态分布,
∴正态曲线的对称轴是直线.
又,
,故选
C.
3.答案:D
解析:因为学生成绩X服从正态分布,所以.
因为,所以,
所以,故选D.
4.答案:B
解析:由正态曲线的对称性知,故选B.
5.答案:D
解析:正态分布密度函数为,则对应函数图象的对称轴为直线.
正态曲线关于直线对称,.
越小曲线越“瘦高”,
函数中的比函数中的要小,函数和的值相等.故选D.
6.答案:C
解析:由正态分布知,每个人数学成绩在的概率为,
所以10个学生数学成绩在的人数服从二项分布,
所以方差为,故选C.
7.答案:C
解析:由题意,数学成绩服从正态分布,且根据正态分布密度曲线的对称性,可得所以0.8)=0.1.所以按成绩分层随机抽样抽取100份试卷时,应从120分以上的试卷中抽取份,故选C.
8.答案:
解析:因为随机变量X服从正态分布且所以由正态曲线的对称性可知解得.
9.答案:0.954
解析:∵随机变量X服从正态分布,
∴正态分布密度曲线关于直线对称.
.
.
10.答案:(1)利用测量数据,即可计算平均值与标准差.
.
.
(2)需要进一步调试.服从正态分布,
,
∴内径在之外的概率为0.003,而,根据原则,需要进一步调试.
