1.4课时 空间向量的应用 课时练习 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册word含解析
文档属性
| 名称 | 1.4课时 空间向量的应用 课时练习 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册word含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 11:02:40 | ||
图片预览




文档简介
2021-2022学年高二数学(人教A版(2019)选择性必修一)
1.4课时
空间向量的应用
一、单选题。本大题共8小题,每小题只有一个选项符合题意。
1.已知向量,,且,则的值为
A.-14
B.10
C.12
D.14
2.若在直线l上,则直线l的一个方向向量为(
)
A.
B.
C.
D.
3.在平行六面体中,若,则的值等于(
)
A.
B.
C.
D.
4.若向量为两个非零向量,且,则向量与的夹角为
A.
B.
C.
D.
5.平面的一个法向量为,平面的一个法向量,则平面与平面(
)
A.平行
B.垂直
C.相交
D.不能确定
6.若平面的法向量分别为,则(
)
A.
B.与相交但不垂直
C.
D.或与重合
7.如图,设是正方形所在平面外一点,且平面,则平面与平面、平面所在平面的位置关系是(
)
A.平面与平面平面都垂直
B.它们两两垂直
C.平面与平面垂直,与平面不垂直
D.平面与平面、平面都不垂直
8.在长方体中,,,分别为棱,,的中点,,则异面直线与所成角的大小为(
)
A.
B.
C.
D.
二、多选题。本大题共4小题,每小题有两项或以上符合题意。
9.已知A,B,C三点不共线,O为平面ABC外的任一点,则“点M与点A,B,C共面”的充分条件的是(
)
A.
B.
C.
D.
10.正方体ABCD?A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则(
)
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
11.三棱锥中,平面与平面的法向量分别为,若,则二面角的大小可能为(
)
A.
B.
C.
D.
12.将正方形沿对角线折成直二面角,有如下四个结论:①;②
是等边三角形;③与平面所成的角为;④与所成的角为.其中正确的结论有(
)
A.①
B.②
C.③
D.④
三、填空题。本大题共4小题。
13.如图所示,ABCD-EFGH为边长等于1的正方体,若P点在正方体的内部且满足,则P点到直线AB的距离为________.
14.将边长为1,A=60°的菱形ABDC沿对角线BC折成直二面角,则二面角A-BD-C的正弦值为________.
15.已知分别是平面α,β,γ的法向量,则α,β,γ三个平面中互相垂直的有________对.
16.已知直线l与平面α垂直,直线l的一个方向向量为=(1,-3,z),向量=(3,-2,1)与平面α平行,则z=________.
四、解答题。本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程。
17.在多面体中,正方形和矩形互相垂直,、分别是和的中点,.
(1)求证:平面.
(2)在边所在的直线上存在一点,使得平面,求的长;
18.如图所示,平面CDEF平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,EDCD,AB=3EF=3,ED=a,AD.
(1)求证:ADBF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求的值;
19.如图,在四棱锥S﹣ABCD中,已知AB∥DC,AB⊥AD,△SAD是正三角形,且平面SAD⊥平面ABCD,AD=AB=2DC=2,F为SB的中点
(1)求异面直线SA与FC所成角的大小;
(2)在棱SB上是否存在点Q,使平面SAC与平面QAC所成的锐二面角为?若存在,求出的大小;若不存在,请说明理由.
20.如图所示,在直三棱柱ABCA1B1C1中,AB⊥BC,AB=BC=2,BB1=1,E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
21.如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
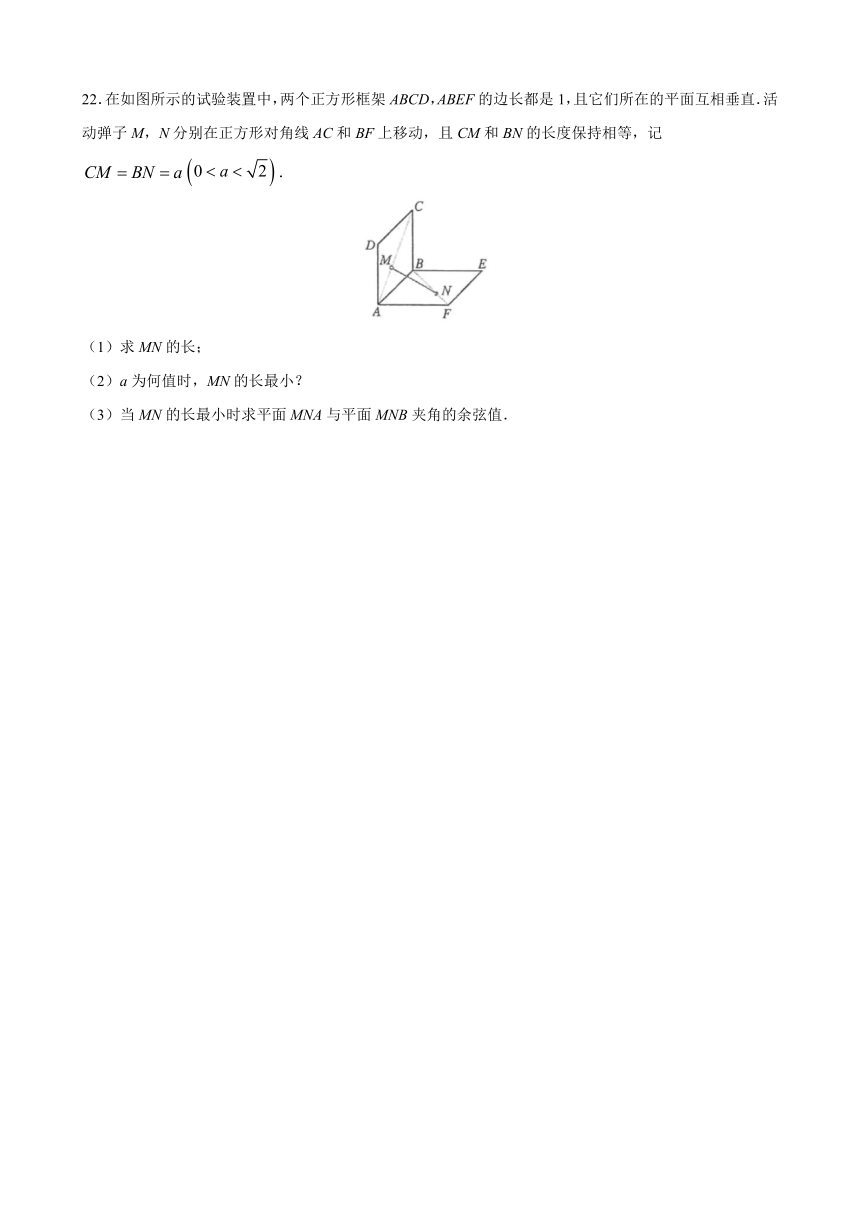
22.在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是1,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF上移动,且CM和BN的长度保持相等,记.
(1)求MN的长;
(2)a为何值时,MN的长最小?
(3)当MN的长最小时求平面MNA与平面MNB夹角的余弦值.
参考答案
1.C
【解析】由题意,向量,,且,
则,解得,故选C.
则的值为(
)
2.A
【解析】由已知得,
故选项A中的向量与共线,是直线的一个方向向量.
故选:A.
3.A
【解析】可知在平行六面体中,,
,
又,
,即,
.
故选:A.
4.A
【解析】作,以OA,OB为邻边作平行四边形OACB,
则,∠AOC为向量与的夹角.
因为,
所以△OAB是等边三角形,平行四边形OACB是菱形,
所以.选A.
5.A
【解析】解:因为平面的一个法向量为,平面的一个法向量,
所以,所以
所以.
故选:A
6.D
【解析】由题意,向量,可得,
所以平面的法向量共线,故或与重合.
故选:D.
7.A
【解析】∵平面,平面,∴.
又∵,,∴平面.
∵平面,平面平面.
∵,∴平面.
∵平面,∴平面平面.
由已知易得平面与平面不垂直,故选A.
8.C
【解析】以为坐标原点,分别以,,的方向为轴、轴、
轴的正方向建立空间直角坐标系,如图
设,则,,,,
所以,,,
所以,所以异面直线与所成角的大小为,
故选:C
9.BD
【解析】当时,可知点与点共面,
所以,
所以,
所以,
不妨令,,,且此时,
因为,,,,
由上可知:BD满足要求.
故选:BD.
10.BC
【解析】根据题意,假设直线D1D与直线AF垂直,又,平面AEF,所以平面AEF,所以,又,所以,与矛盾,所以直线D1D与直线AF不垂直,所以选项A错误;
因为A1G∥D1F,A1G?平面AEFD1,平面AEFD1,所以A1G∥平面AEFD1,故选项B正确.
平面AEF截正方体所得截面为等腰梯形AEFD1,由题得该等腰梯形的上底下底,腰长为,所以梯形面积为,故选项C正确;
假设与到平面的距离相等,即平面将平分,则平面必过的中点,连接交于,而不是中点,则假设不成立,故选项D错误.
故选:BC.
11.BC
【解析】二面角的大小与法向量的夹角相等或互补,
二面角的大小可能为或.
故选:BC.
12.ABD
【解析】解:取中点,由正方形的性质得:,
所以为二面角的平面角,
因为二面角是直二面角,
所以如图所示,建立空间直角坐标系Oxyz,
设正方形的边长为,
则
所以,,,,,
因为=0,故,①正确.
又,,,
所以为等边三角形,②正确.
对于③,为平面的一个法向量,
.
因为直线与平面所成的角的取值范围是,
所以与平面所成的角为,故③错误.
又,
因为异面直线所成的角为锐角或直角,所以与所成的角为,故④正确.
故选:ABD
13.
【解析】解析:过P作PM⊥平面ABCD于M,过M作MN⊥AB于N,连接PN,则PN即为所求,如图所示.
因为,
所以,
所以.
即P点到直线AB的距离为.
故答案为:.
14.
【解析】取BC中点O,连接AO,DO,建立如图所示的空间直角坐标系,
则A,B,D.
所以,,.
由于为平面BCD的一个法向量,
设平面ABD的一个法向量
(x,y,z),
则 所以
取x=1,则y=-,z=1,
所以
(1,-,1)是平面ABD的一个法向量,
所以,
所以二面角A-BD-C的正弦值为.
15.0
【解析】因为,
,
.
所以中任意两个向量都不垂直,即α,β,γ中任意两个平面都不垂直.
故答案为:0.
16.-9
【解析】因为l⊥α,所以⊥,所以(1,-3,z)·(3,-2,1)=0,即3+6+z=0,所以z=-9.
故答案为:-9
17.(1)证明见解析;(2).
【解析】(1)因为四边形为矩形,则,
因为平面平面,平面平面,平面,
所以,平面;
(2)因为平面,四边形为正方形,
以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、,设点,
,,,
设平面的法向量为,
由,令,可得,
要使得平面,则,所以,,解得,
则,此时,.
18.(1)证明见解析;(2).
【解析】(1)∵面CDEF面ABCD,EDCD,面,面面,
∴ED面ABCD,面,即,
过作于,过作交于,
∵CDEF为直角梯形,AB=3EF=3,
∴,即,则,且,
∴,得,即,
∴,而,即面,又面,
∴,故.
(2)以D为原点,过点D垂直于DC的直线为x轴,DC所在直线为y轴,所在直线为z轴,建立空间直角坐标系,如下图示:
∴,若,则,
设,则,
设平面BDM的法向量为,则,取x1=2,则,
若AE∥平面BDM,则,解得,
∴线段CF上存在一点M,满足AE∥平面BDM,此时.
19.(1)90°;(2)存在,1.
【解析】解:(1)∵在四棱锥S﹣ABCD中,已知AB∥DC,AB⊥AD,△SAD是正三角形,
平面SAD⊥平面ABCD,AD=AB=2DC=2,F为SB的中点,
∴以A为原点,AB为x轴,AD为y轴,过A作平面ABCD的垂线为z轴,建立空间直角坐标系,
则A(0,0,0),S(0,1,),C(1,2,0),B(2,0,0),F(1,),
(0,﹣1,),(0,,),
设异面直线SA与FC所成角为θ(0°<θ≤90°),
则cosθ0,∴θ=90°.
∴异面直线SA与FC所成角的大小为90°;
(2)假设在棱SB上存在点Q(a,b,c),λ,(0≤λ≤1),使平面SAC与平面QAC所成的锐二面角为,
则,即(a,b﹣1,c)=λ(2,﹣1,),解得a=2λ,b=1﹣λ,c,
∴Q(2λ,1﹣λ,),(2λ,1﹣λ,),(1,2,0),(0,1,),
设平面ACQ的法向量(x,y,z),
则,取x=2,得,
设平面ASC的法向量(p,q,r),
则,取p=2,得=(2,﹣1,),
∵平面SAC与平面QAC所成的锐二面角为,
∴,
整理得5λ2﹣10λ+4=0,解得λ或(舍去).
故在棱SB上存在点Q,使平面SAC与平面QAC所成的锐二面角为,此时.
20.证明见解析
【解析】由题意得AB,BC,B1B两两垂直.以B为原点,BA,BC,BB1分别为x,y,z轴,建立如图所示的空间直角坐标系.
则A(2,0,0),A1(2,0,1),C(0,2,0),C1(0,2,1),E,
则=(0,0,1),=(-2,2,0),=(-2,2,1),=.
设平面AA1C1C的一个法向量为=(x1,y1,z1).
则
令x1=1,得y1=1.∴=(1,1,0).
设平面AEC1的一个法向量为=(x2,y2,z2).
则?
令z2=4,得x2=1,y2=-1.∴=(1,-1,4).
∵=1×1+1×(-1)+0×4=0.
∴,∴平面AEC1⊥平面AA1C1C.
21.(1)证明见解析;(2)G为AD的中点,证明见解析.
【解析】(1)证明 如图,以D为原点,分别以DA,DC,DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设AD=a,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),E,P(0,0,a),F.
=,=(0,a,0).
∵=0,∴,即EF⊥CD.
(2)解:设G(x,0,z),则=,
若使GF⊥平面PCB,则需且
由=·(a,0,0)
=a=0,得x=;
由=·(0,-a,a)
=+a=0,得z=0.
∴G点坐标为,即G为AD的中点.
22.(1);(2)时,最小,最小值为;(3)
【解析】解:如图建立空间直角坐标系,
,,
,
,
,,
.
(1);
(2),
当时,最小,最小值为;
(3)由(2)可知,当,为中点时,最短,
则,0,,,,,取的中点,连接,,
则,,,
,,,,
是平面与平面的夹角或其补角.
,,
.
平面与平面夹角的余弦值是.
1.4课时
空间向量的应用
一、单选题。本大题共8小题,每小题只有一个选项符合题意。
1.已知向量,,且,则的值为
A.-14
B.10
C.12
D.14
2.若在直线l上,则直线l的一个方向向量为(
)
A.
B.
C.
D.
3.在平行六面体中,若,则的值等于(
)
A.
B.
C.
D.
4.若向量为两个非零向量,且,则向量与的夹角为
A.
B.
C.
D.
5.平面的一个法向量为,平面的一个法向量,则平面与平面(
)
A.平行
B.垂直
C.相交
D.不能确定
6.若平面的法向量分别为,则(
)
A.
B.与相交但不垂直
C.
D.或与重合
7.如图,设是正方形所在平面外一点,且平面,则平面与平面、平面所在平面的位置关系是(
)
A.平面与平面平面都垂直
B.它们两两垂直
C.平面与平面垂直,与平面不垂直
D.平面与平面、平面都不垂直
8.在长方体中,,,分别为棱,,的中点,,则异面直线与所成角的大小为(
)
A.
B.
C.
D.
二、多选题。本大题共4小题,每小题有两项或以上符合题意。
9.已知A,B,C三点不共线,O为平面ABC外的任一点,则“点M与点A,B,C共面”的充分条件的是(
)
A.
B.
C.
D.
10.正方体ABCD?A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则(
)
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
11.三棱锥中,平面与平面的法向量分别为,若,则二面角的大小可能为(
)
A.
B.
C.
D.
12.将正方形沿对角线折成直二面角,有如下四个结论:①;②
是等边三角形;③与平面所成的角为;④与所成的角为.其中正确的结论有(
)
A.①
B.②
C.③
D.④
三、填空题。本大题共4小题。
13.如图所示,ABCD-EFGH为边长等于1的正方体,若P点在正方体的内部且满足,则P点到直线AB的距离为________.
14.将边长为1,A=60°的菱形ABDC沿对角线BC折成直二面角,则二面角A-BD-C的正弦值为________.
15.已知分别是平面α,β,γ的法向量,则α,β,γ三个平面中互相垂直的有________对.
16.已知直线l与平面α垂直,直线l的一个方向向量为=(1,-3,z),向量=(3,-2,1)与平面α平行,则z=________.
四、解答题。本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程。
17.在多面体中,正方形和矩形互相垂直,、分别是和的中点,.
(1)求证:平面.
(2)在边所在的直线上存在一点,使得平面,求的长;
18.如图所示,平面CDEF平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,EDCD,AB=3EF=3,ED=a,AD.
(1)求证:ADBF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求的值;
19.如图,在四棱锥S﹣ABCD中,已知AB∥DC,AB⊥AD,△SAD是正三角形,且平面SAD⊥平面ABCD,AD=AB=2DC=2,F为SB的中点
(1)求异面直线SA与FC所成角的大小;
(2)在棱SB上是否存在点Q,使平面SAC与平面QAC所成的锐二面角为?若存在,求出的大小;若不存在,请说明理由.
20.如图所示,在直三棱柱ABCA1B1C1中,AB⊥BC,AB=BC=2,BB1=1,E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
21.如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
22.在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是1,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF上移动,且CM和BN的长度保持相等,记.
(1)求MN的长;
(2)a为何值时,MN的长最小?
(3)当MN的长最小时求平面MNA与平面MNB夹角的余弦值.
参考答案
1.C
【解析】由题意,向量,,且,
则,解得,故选C.
则的值为(
)
2.A
【解析】由已知得,
故选项A中的向量与共线,是直线的一个方向向量.
故选:A.
3.A
【解析】可知在平行六面体中,,
,
又,
,即,
.
故选:A.
4.A
【解析】作,以OA,OB为邻边作平行四边形OACB,
则,∠AOC为向量与的夹角.
因为,
所以△OAB是等边三角形,平行四边形OACB是菱形,
所以.选A.
5.A
【解析】解:因为平面的一个法向量为,平面的一个法向量,
所以,所以
所以.
故选:A
6.D
【解析】由题意,向量,可得,
所以平面的法向量共线,故或与重合.
故选:D.
7.A
【解析】∵平面,平面,∴.
又∵,,∴平面.
∵平面,平面平面.
∵,∴平面.
∵平面,∴平面平面.
由已知易得平面与平面不垂直,故选A.
8.C
【解析】以为坐标原点,分别以,,的方向为轴、轴、
轴的正方向建立空间直角坐标系,如图
设,则,,,,
所以,,,
所以,所以异面直线与所成角的大小为,
故选:C
9.BD
【解析】当时,可知点与点共面,
所以,
所以,
所以,
不妨令,,,且此时,
因为,,,,
由上可知:BD满足要求.
故选:BD.
10.BC
【解析】根据题意,假设直线D1D与直线AF垂直,又,平面AEF,所以平面AEF,所以,又,所以,与矛盾,所以直线D1D与直线AF不垂直,所以选项A错误;
因为A1G∥D1F,A1G?平面AEFD1,平面AEFD1,所以A1G∥平面AEFD1,故选项B正确.
平面AEF截正方体所得截面为等腰梯形AEFD1,由题得该等腰梯形的上底下底,腰长为,所以梯形面积为,故选项C正确;
假设与到平面的距离相等,即平面将平分,则平面必过的中点,连接交于,而不是中点,则假设不成立,故选项D错误.
故选:BC.
11.BC
【解析】二面角的大小与法向量的夹角相等或互补,
二面角的大小可能为或.
故选:BC.
12.ABD
【解析】解:取中点,由正方形的性质得:,
所以为二面角的平面角,
因为二面角是直二面角,
所以如图所示,建立空间直角坐标系Oxyz,
设正方形的边长为,
则
所以,,,,,
因为=0,故,①正确.
又,,,
所以为等边三角形,②正确.
对于③,为平面的一个法向量,
.
因为直线与平面所成的角的取值范围是,
所以与平面所成的角为,故③错误.
又,
因为异面直线所成的角为锐角或直角,所以与所成的角为,故④正确.
故选:ABD
13.
【解析】解析:过P作PM⊥平面ABCD于M,过M作MN⊥AB于N,连接PN,则PN即为所求,如图所示.
因为,
所以,
所以.
即P点到直线AB的距离为.
故答案为:.
14.
【解析】取BC中点O,连接AO,DO,建立如图所示的空间直角坐标系,
则A,B,D.
所以,,.
由于为平面BCD的一个法向量,
设平面ABD的一个法向量
(x,y,z),
则 所以
取x=1,则y=-,z=1,
所以
(1,-,1)是平面ABD的一个法向量,
所以,
所以二面角A-BD-C的正弦值为.
15.0
【解析】因为,
,
.
所以中任意两个向量都不垂直,即α,β,γ中任意两个平面都不垂直.
故答案为:0.
16.-9
【解析】因为l⊥α,所以⊥,所以(1,-3,z)·(3,-2,1)=0,即3+6+z=0,所以z=-9.
故答案为:-9
17.(1)证明见解析;(2).
【解析】(1)因为四边形为矩形,则,
因为平面平面,平面平面,平面,
所以,平面;
(2)因为平面,四边形为正方形,
以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、,设点,
,,,
设平面的法向量为,
由,令,可得,
要使得平面,则,所以,,解得,
则,此时,.
18.(1)证明见解析;(2).
【解析】(1)∵面CDEF面ABCD,EDCD,面,面面,
∴ED面ABCD,面,即,
过作于,过作交于,
∵CDEF为直角梯形,AB=3EF=3,
∴,即,则,且,
∴,得,即,
∴,而,即面,又面,
∴,故.
(2)以D为原点,过点D垂直于DC的直线为x轴,DC所在直线为y轴,所在直线为z轴,建立空间直角坐标系,如下图示:
∴,若,则,
设,则,
设平面BDM的法向量为,则,取x1=2,则,
若AE∥平面BDM,则,解得,
∴线段CF上存在一点M,满足AE∥平面BDM,此时.
19.(1)90°;(2)存在,1.
【解析】解:(1)∵在四棱锥S﹣ABCD中,已知AB∥DC,AB⊥AD,△SAD是正三角形,
平面SAD⊥平面ABCD,AD=AB=2DC=2,F为SB的中点,
∴以A为原点,AB为x轴,AD为y轴,过A作平面ABCD的垂线为z轴,建立空间直角坐标系,
则A(0,0,0),S(0,1,),C(1,2,0),B(2,0,0),F(1,),
(0,﹣1,),(0,,),
设异面直线SA与FC所成角为θ(0°<θ≤90°),
则cosθ0,∴θ=90°.
∴异面直线SA与FC所成角的大小为90°;
(2)假设在棱SB上存在点Q(a,b,c),λ,(0≤λ≤1),使平面SAC与平面QAC所成的锐二面角为,
则,即(a,b﹣1,c)=λ(2,﹣1,),解得a=2λ,b=1﹣λ,c,
∴Q(2λ,1﹣λ,),(2λ,1﹣λ,),(1,2,0),(0,1,),
设平面ACQ的法向量(x,y,z),
则,取x=2,得,
设平面ASC的法向量(p,q,r),
则,取p=2,得=(2,﹣1,),
∵平面SAC与平面QAC所成的锐二面角为,
∴,
整理得5λ2﹣10λ+4=0,解得λ或(舍去).
故在棱SB上存在点Q,使平面SAC与平面QAC所成的锐二面角为,此时.
20.证明见解析
【解析】由题意得AB,BC,B1B两两垂直.以B为原点,BA,BC,BB1分别为x,y,z轴,建立如图所示的空间直角坐标系.
则A(2,0,0),A1(2,0,1),C(0,2,0),C1(0,2,1),E,
则=(0,0,1),=(-2,2,0),=(-2,2,1),=.
设平面AA1C1C的一个法向量为=(x1,y1,z1).
则
令x1=1,得y1=1.∴=(1,1,0).
设平面AEC1的一个法向量为=(x2,y2,z2).
则?
令z2=4,得x2=1,y2=-1.∴=(1,-1,4).
∵=1×1+1×(-1)+0×4=0.
∴,∴平面AEC1⊥平面AA1C1C.
21.(1)证明见解析;(2)G为AD的中点,证明见解析.
【解析】(1)证明 如图,以D为原点,分别以DA,DC,DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设AD=a,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),E,P(0,0,a),F.
=,=(0,a,0).
∵=0,∴,即EF⊥CD.
(2)解:设G(x,0,z),则=,
若使GF⊥平面PCB,则需且
由=·(a,0,0)
=a=0,得x=;
由=·(0,-a,a)
=+a=0,得z=0.
∴G点坐标为,即G为AD的中点.
22.(1);(2)时,最小,最小值为;(3)
【解析】解:如图建立空间直角坐标系,
,,
,
,
,,
.
(1);
(2),
当时,最小,最小值为;
(3)由(2)可知,当,为中点时,最短,
则,0,,,,,取的中点,连接,,
则,,,
,,,,
是平面与平面的夹角或其补角.
,,
.
平面与平面夹角的余弦值是.
