坐标系与参数方程学案
图片预览




文档简介
极坐标系的概念
如图,在平面上取一定点,从引一条射线,再取定一个单位长度并规定旋转的正方向,这样就构成了一个极坐标系,点称为极点,射线称为极轴
设为平面上任意一点,连接令,表示从到的角,称为点的极径,称为点的极角,这一对有序实数与称为点的极坐标 记做:
和的性质
当时表示极点,时表示极轴上的点
当时,在角的终边上取点使
当时,则在角的终边的反向延长线上取点,使如下图
巩固练习 请自己建立极坐标系,分别标出四个点,并观察它们的位置关系
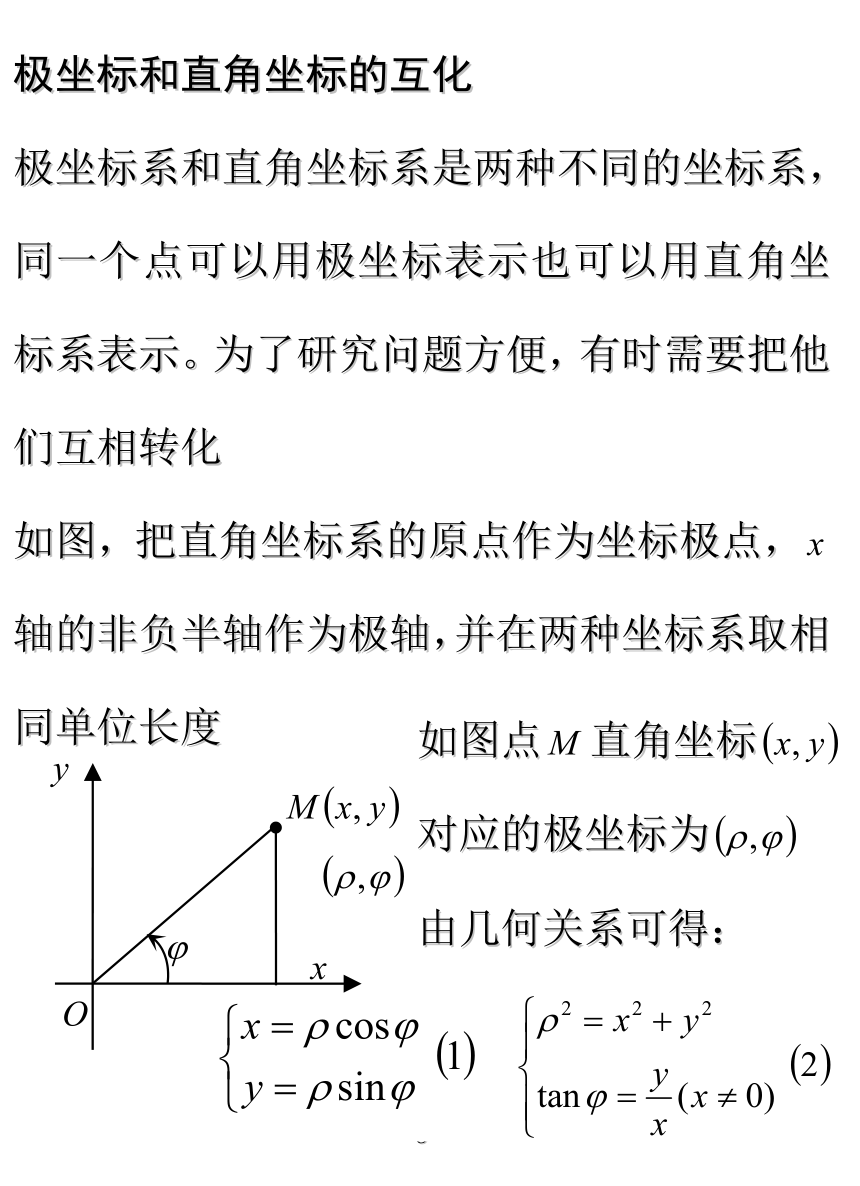
极坐标和直角坐标的互化
极坐标系和直角坐标系是两种不同的坐标系,同一个点可以用极坐标表示也可以用直角坐标系表示。为了研究问题方便,有时需要把他们互相转化
如图,把直角坐标系的原点作为坐标极点,轴的非负半轴作为极轴,并在两种坐标系取相同单位长度
坐标互化与方程互化方法
极系坐标化成直角系坐标——利用公式(1)
直角系坐标化成极系坐标——利用公式(2)
直系方程化成极系方程——代换法
极系方程化成直系方程——拼凑法
巩固练习 在极坐标系中,已知两点 ,,求两点间的距离
设点对应的复数为,以原点为极点,实轴正半轴为极轴建立极坐标系,求点的极坐标
例:将圆化为极坐标方程
解:由公式(1)得:
(代换法)
所以 或
因为表示点圆与矛盾,(舍去)
所求极坐标方程为
例:将极坐标方程化为直角坐标方程
解:将 两边同乘以得:
即 (拼凑法)
巩固练习 已知直线的极坐标方程为 ,求点到直线的距离
简单曲线的极坐标方程
1.求极坐标方程表示的曲线
2.已知点的极坐标是,则过点且垂直极轴的直线方程是( )
B. C. D.
3.如果直线与直线关于极轴对称,则直线的极坐标方程是( )
A. B.
C. D.
提示:两直线关于极轴对称,说明两直线极角一正一负,即两直线的斜率互为相反数
设过原点的直线与圆的一个交点为,点为线段的中点。
(I)求圆的极坐标方程;(II)求点的轨迹方程,并说明它是什么曲线
提示:(I)容易得圆的极坐标方程为(II)设点和的极坐标分别为
因点为线段的中点,所以
将代入,得
所以点轨迹的极坐标方程为
它表示圆心在,半径为的圆
学习解答此题的步骤,培养规范的做题习惯
在直角坐标系中,以为极点,轴的正半轴为极轴的极坐标系中,曲线的极坐标方程为,曲线的极坐标方程为,射线与的异于极点的交点为,与的异于极点的交点为,求
提示:
射线与的交点的极径为
射线与的交点的极径为
由极径的几何意义可知:
准确理解定义及几何意义,高中阶段考察重点
在直角坐标系中,以为极点,轴的正半轴为极轴的极坐标系中,曲线的极坐标方程为,分别为与轴和轴的交点。(I)写出的直角坐标方程,并求两点的极坐标;(II)设的中点为,求直线的极坐标方程
提示:(I)的直角坐标方程为
当时所以同理求得
(II)直线的极坐标方程:
综合题考察的是我们对基础知识运用能力
能力提升 抛物线的极坐标方程为,过原点作互相垂直的两条直线分别交此抛物线于和四点,当两条直线的倾斜角为何值时,有最小值?并求出这个最小值
提示:设
则
所以当即或时
有最小值16
题型练习提炼总结形成通性思维得分参数方程
在实际应用中有些曲线用直角坐标系或极坐标系内的流动坐标或来表示比较困难,也就是说很难找到曲线所满足的或的式子,为此我们引入一个新的变量来表示曲线方程,即:参数方程
例:如12页图,建立直角坐标系,设点为炮弹在运动中的任意位置,可以看出要有和之间的直接关系来表示炮弹运动的轨迹方程比较困难。
但我们发现: 炮弹运动的轨迹由炮弹在各时刻的位置所决定的
分析炮弹在任意位置的坐标和与时刻之间的关系.
其中表示重力加速度,是炮弹落地的时刻;
在上连续变化时,就描绘了炮弹运动的轨迹。
用流动坐标或和另一个变量表示的方程,叫参数方程
参数方程与普通方程的互化
普通方程化参数方程在曲线中应用较少,但在直线方程中却有很好的应用
消参时需掌握的几点:
(I)曲线参数方程中,注意利用
(II)消参时注意取值范围的限定
(III)几种需先平方后消参的参数方程
1.下列在曲线上的点
B. C. D.
提示:需先将参数方程化成普通方程,对
平方,易得方程,代入验证
求下列参数方程的普通方程
I. II.
提示:注参数本身的取值范围和对的限定
参数方程为表示什么图形
提示:表示平行于轴的两条射线
参数方程表示的曲线是
提示:化成普通方程为
方程的曲线是
提示:根据的限定范围可得
参数方程表示什么曲线
提示:根据三角恒等消参法容易算出
直线截所得的弦长
提示:常规方法将直线化成普通方程与圆方程联立求得两点坐标,再利用两点距离公式
那么你能想出更简单的方法么
圆和椭圆的参数方程见教材
圆的参数方程为:
,参数表示终边转角
椭圆椭圆参数方程为:
,参数表示离心角
已知点是圆上的动点.
求的取值范围
若恒成立,求实数的取值范围
提示:设圆的参数方程为利用三角函数式求的最小值,求得
基础题不一定做得正确,要重视知识的连贯性
2.已知是椭圆与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点,使四边形的面积最大
提示:,其中为定值只需为最大值,即找一点到的距离最大
即时最大,求得
认真审题,锤炼自己的通性思维更敏捷准确
直线的参数方程
直线参数几何意义应用时需注意的几个问题
直线的标准式参数方程里:直线恒过定点,倾斜角为,参数的绝对值等于直线上动点到定点的距离即,此时若,则
的方向向上,若,则的方向向下
认清直线参数方程的标准式和一般式里参数的几何意义;一般式的参数方程里,当时
抓住问题的实质,在做题时就不会模棱两可
直线参数方程标准式的常用结论
设过点倾斜角为的直线的参数方程为若是上两点
则有:(I) (II)线段中点到定点的距离 (III)若是线段的中点,则
例:再回头来看第七题
解:将代入
得 弦长为
厘清解题方法,有助于提高做答速度和准确率
已知直线与抛物线交于两点,求点到两点的距离积
提示:设的参数方程为 那么点到两点的距离积为
2. 经过点作直线,交椭圆于两点,如果点恰好为线段的中点,求直线的方程
提示:首先设直线的参数方程然后代入椭圆
由题意得,求倾斜角再求直线方程
千里之行始于足下,在学习中培养做事的态度
如图点直角坐标
对应的极坐标为
由几何关系可得:
1
如图,在平面上取一定点,从引一条射线,再取定一个单位长度并规定旋转的正方向,这样就构成了一个极坐标系,点称为极点,射线称为极轴
设为平面上任意一点,连接令,表示从到的角,称为点的极径,称为点的极角,这一对有序实数与称为点的极坐标 记做:
和的性质
当时表示极点,时表示极轴上的点
当时,在角的终边上取点使
当时,则在角的终边的反向延长线上取点,使如下图
巩固练习 请自己建立极坐标系,分别标出四个点,并观察它们的位置关系
极坐标和直角坐标的互化
极坐标系和直角坐标系是两种不同的坐标系,同一个点可以用极坐标表示也可以用直角坐标系表示。为了研究问题方便,有时需要把他们互相转化
如图,把直角坐标系的原点作为坐标极点,轴的非负半轴作为极轴,并在两种坐标系取相同单位长度
坐标互化与方程互化方法
极系坐标化成直角系坐标——利用公式(1)
直角系坐标化成极系坐标——利用公式(2)
直系方程化成极系方程——代换法
极系方程化成直系方程——拼凑法
巩固练习 在极坐标系中,已知两点 ,,求两点间的距离
设点对应的复数为,以原点为极点,实轴正半轴为极轴建立极坐标系,求点的极坐标
例:将圆化为极坐标方程
解:由公式(1)得:
(代换法)
所以 或
因为表示点圆与矛盾,(舍去)
所求极坐标方程为
例:将极坐标方程化为直角坐标方程
解:将 两边同乘以得:
即 (拼凑法)
巩固练习 已知直线的极坐标方程为 ,求点到直线的距离
简单曲线的极坐标方程
1.求极坐标方程表示的曲线
2.已知点的极坐标是,则过点且垂直极轴的直线方程是( )
B. C. D.
3.如果直线与直线关于极轴对称,则直线的极坐标方程是( )
A. B.
C. D.
提示:两直线关于极轴对称,说明两直线极角一正一负,即两直线的斜率互为相反数
设过原点的直线与圆的一个交点为,点为线段的中点。
(I)求圆的极坐标方程;(II)求点的轨迹方程,并说明它是什么曲线
提示:(I)容易得圆的极坐标方程为(II)设点和的极坐标分别为
因点为线段的中点,所以
将代入,得
所以点轨迹的极坐标方程为
它表示圆心在,半径为的圆
学习解答此题的步骤,培养规范的做题习惯
在直角坐标系中,以为极点,轴的正半轴为极轴的极坐标系中,曲线的极坐标方程为,曲线的极坐标方程为,射线与的异于极点的交点为,与的异于极点的交点为,求
提示:
射线与的交点的极径为
射线与的交点的极径为
由极径的几何意义可知:
准确理解定义及几何意义,高中阶段考察重点
在直角坐标系中,以为极点,轴的正半轴为极轴的极坐标系中,曲线的极坐标方程为,分别为与轴和轴的交点。(I)写出的直角坐标方程,并求两点的极坐标;(II)设的中点为,求直线的极坐标方程
提示:(I)的直角坐标方程为
当时所以同理求得
(II)直线的极坐标方程:
综合题考察的是我们对基础知识运用能力
能力提升 抛物线的极坐标方程为,过原点作互相垂直的两条直线分别交此抛物线于和四点,当两条直线的倾斜角为何值时,有最小值?并求出这个最小值
提示:设
则
所以当即或时
有最小值16
题型练习提炼总结形成通性思维得分参数方程
在实际应用中有些曲线用直角坐标系或极坐标系内的流动坐标或来表示比较困难,也就是说很难找到曲线所满足的或的式子,为此我们引入一个新的变量来表示曲线方程,即:参数方程
例:如12页图,建立直角坐标系,设点为炮弹在运动中的任意位置,可以看出要有和之间的直接关系来表示炮弹运动的轨迹方程比较困难。
但我们发现: 炮弹运动的轨迹由炮弹在各时刻的位置所决定的
分析炮弹在任意位置的坐标和与时刻之间的关系.
其中表示重力加速度,是炮弹落地的时刻;
在上连续变化时,就描绘了炮弹运动的轨迹。
用流动坐标或和另一个变量表示的方程,叫参数方程
参数方程与普通方程的互化
普通方程化参数方程在曲线中应用较少,但在直线方程中却有很好的应用
消参时需掌握的几点:
(I)曲线参数方程中,注意利用
(II)消参时注意取值范围的限定
(III)几种需先平方后消参的参数方程
1.下列在曲线上的点
B. C. D.
提示:需先将参数方程化成普通方程,对
平方,易得方程,代入验证
求下列参数方程的普通方程
I. II.
提示:注参数本身的取值范围和对的限定
参数方程为表示什么图形
提示:表示平行于轴的两条射线
参数方程表示的曲线是
提示:化成普通方程为
方程的曲线是
提示:根据的限定范围可得
参数方程表示什么曲线
提示:根据三角恒等消参法容易算出
直线截所得的弦长
提示:常规方法将直线化成普通方程与圆方程联立求得两点坐标,再利用两点距离公式
那么你能想出更简单的方法么
圆和椭圆的参数方程见教材
圆的参数方程为:
,参数表示终边转角
椭圆椭圆参数方程为:
,参数表示离心角
已知点是圆上的动点.
求的取值范围
若恒成立,求实数的取值范围
提示:设圆的参数方程为利用三角函数式求的最小值,求得
基础题不一定做得正确,要重视知识的连贯性
2.已知是椭圆与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点,使四边形的面积最大
提示:,其中为定值只需为最大值,即找一点到的距离最大
即时最大,求得
认真审题,锤炼自己的通性思维更敏捷准确
直线的参数方程
直线参数几何意义应用时需注意的几个问题
直线的标准式参数方程里:直线恒过定点,倾斜角为,参数的绝对值等于直线上动点到定点的距离即,此时若,则
的方向向上,若,则的方向向下
认清直线参数方程的标准式和一般式里参数的几何意义;一般式的参数方程里,当时
抓住问题的实质,在做题时就不会模棱两可
直线参数方程标准式的常用结论
设过点倾斜角为的直线的参数方程为若是上两点
则有:(I) (II)线段中点到定点的距离 (III)若是线段的中点,则
例:再回头来看第七题
解:将代入
得 弦长为
厘清解题方法,有助于提高做答速度和准确率
已知直线与抛物线交于两点,求点到两点的距离积
提示:设的参数方程为 那么点到两点的距离积为
2. 经过点作直线,交椭圆于两点,如果点恰好为线段的中点,求直线的方程
提示:首先设直线的参数方程然后代入椭圆
由题意得,求倾斜角再求直线方程
千里之行始于足下,在学习中培养做事的态度
如图点直角坐标
对应的极坐标为
由几何关系可得:
1
