【精品练习】人教A版 数学 选修2第1章1.7.2知能优化训练
文档属性
| 名称 | 【精品练习】人教A版 数学 选修2第1章1.7.2知能优化训练 |
|
|
| 格式 | zip | ||
| 文件大小 | 148.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-09 00:00:00 | ||
图片预览

文档简介
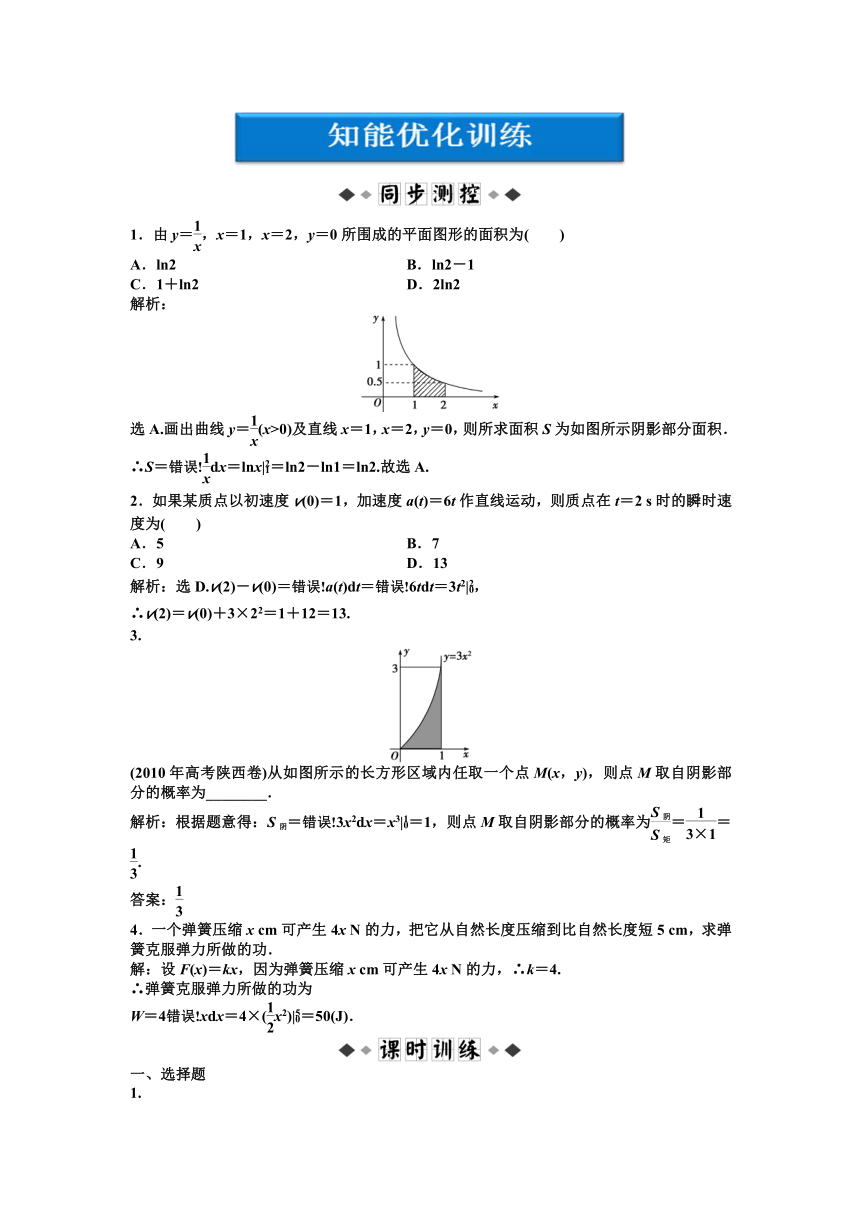
1.由y=,x=1,x=2,y=0所围成的平面图形的面积为( )
A.ln2 B.ln2-1
C.1+ln2 D.2ln2
解析:
选A.画出曲线y=(x>0)及直线x=1,x=2,y=0,则所求面积S为如图所示阴影部分面积.
∴S=dx=lnx|=ln2-ln1=ln2.故选A.
2.如果某质点以初速度v(0)=1,加速度a(t)=6t作直线运动,则质点在t=2 s时的瞬时速度为( )
A.5 B.7
C.9 D.13
解析:选D.v(2)-v(0)=a(t)dt=6tdt=3t2|,
∴v(2)=v(0)+3×22=1+12=13.
3.
(2010年高考陕西卷)从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为________.
解析:根据题意得:S阴=3x2dx=x3|=1,则点M取自阴影部分的概率为==.
答案:
4.一个弹簧压缩x cm可产生4x N的力,把它从自然长度压缩到比自然长度短5 cm,求弹簧克服弹力所做的功.
解:设F(x)=kx,因为弹簧压缩x cm可产生4x N的力,∴k=4.
∴弹簧克服弹力所做的功为
W=4xdx=4×(x2)|=50(J).
一、选择题
1.
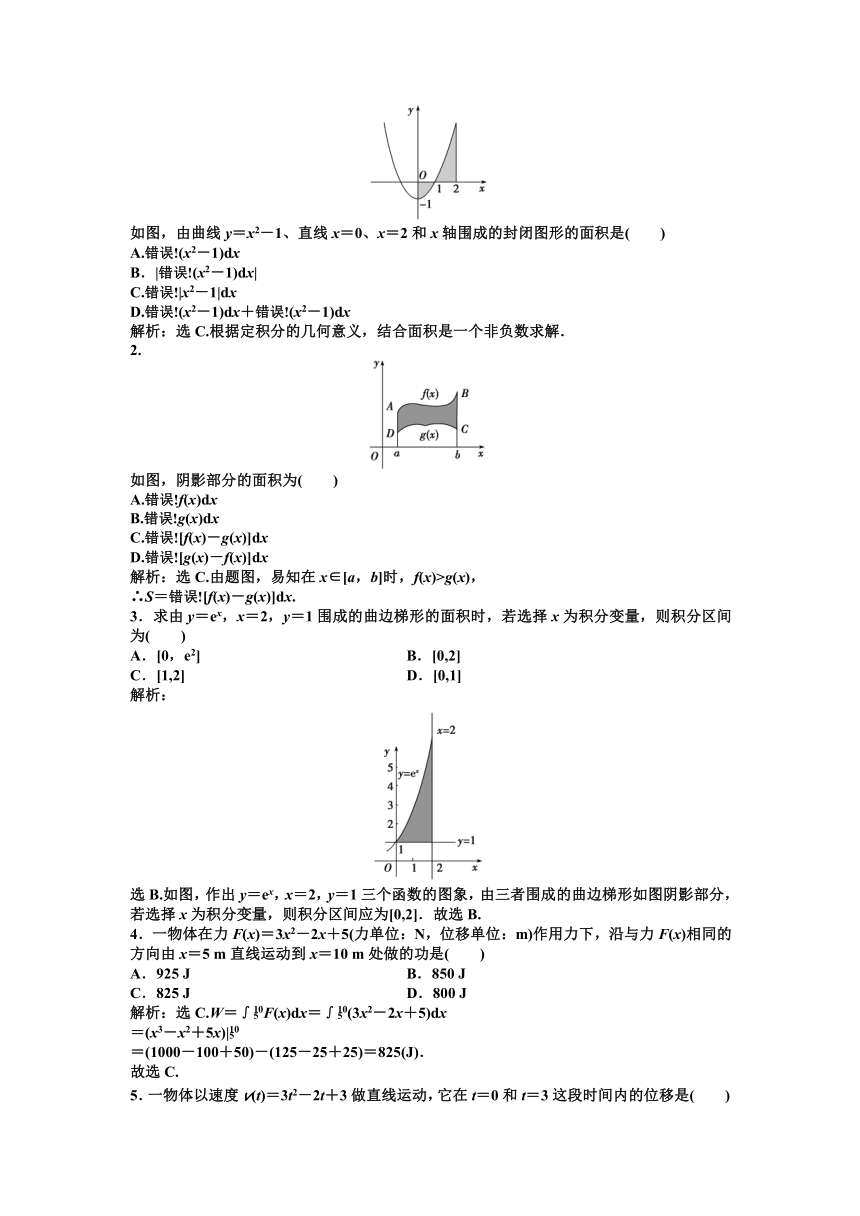
如图,由曲线y=x2-1、直线x=0、x=2和x轴围成的封闭图形的面积是( )
A.(x2-1)dx
B.|(x2-1)dx|
C.|x2-1|dx
D.(x2-1)dx+(x2-1)dx
解析:选C.根据定积分的几何意义,结合面积是一个非负数求解.
2.
如图,阴影部分的面积为( )
A.f(x)dx
B.g(x)dx
C.[f(x)-g(x)]dx
D.[g(x)-f(x)]dx
解析:选C.由题图,易知在x∈[a,b]时,f(x)>g(x),
∴S=[f(x)-g(x)]dx.
3.求由y=ex,x=2,y=1围成的曲边梯形的面积时,若选择x为积分变量,则积分区间为( )
A.[0,e2] B.[0,2]
C.[1,2] D.[0,1]
解析:
选B.如图,作出y=ex,x=2,y=1三个函数的图象,由三者围成的曲边梯形如图阴影部分,若选择x为积分变量,则积分区间应为[0,2].故选B.
4.一物体在力F(x)=3x2-2x+5(力单位:N,位移单位:m)作用力下,沿与力F(x)相同的方向由x=5 m直线运动到x=10 m处做的功是( )
A.925 J B.850 J
C.825 J D.800 J
解析:选C.W=∫F(x)dx=∫(3x2-2x+5)dx
=(x3-x2+5x)|
=(1000-100+50)-(125-25+25)=825(J).
故选C.
5.一物体以速度v(t)=3t2-2t+3做直线运动,它在t=0和t=3这段时间内的位移是( )
A.9 B.18
C.27 D.36
解析:选C.s=v(t)dt=(3t2-2t+3)dt=(t3-t2+3t)|=33-32+3×3-0=27.故选C.
6.一物体在力F(x)=(单位:N)的作用下沿与力F相同的方向作直线运动,从x=0处运动到x=4(单位:m)处,则力F(x)作的功为( )
A.44 J B.46 J
C.48 J D.50 J
解析:选B.W=F(x)dx=10dx+(3x+4)dx=10x|+(x2+4x)|=46(J).故选B.
二、填空题
7.若1 N的力能使弹簧伸长2 cm,则使弹簧伸长12 cm时克服弹力所作的功为________.
解析:弹簧的伸长与所受到的拉力成正比,设F=kx,求得k=50,∴F(x)=50x.
∴W=∫50xdx=25x2|=0.36(J).
答案:0.36 J
8.有一横截面的面积为4 cm2的水管控制往外流水,打开水管后t秒末的流速为v(t)=6t-t2(单位:cm/s)(0≤t≤6).则t=0到t=6这段时间内流出的水量为________.
解析:由题意可得t=0到t=6这段时间内流出的水量V=4(6t-t2)dt=4(6t-t2)dt=4(3t2-t3)|=144(cm3).故t=0到t=6这段时间内流出的水量为144 cm3.
答案:144 cm3
9.由曲线y=x2+4与直线y=5x,x=0,x=4所围成平面图形的面积是________.
解析:
由得x=1或x=4.
所求面积为S=(x2+4-5x)dx+(5x-x2-4)dx
=(x3+4x-x2)|+(x2-x3-4x)|=.
答案:
三、解答题
10.
一物体做变速直线运动,其v-t曲线如图所示,求该物体在 s~6 s间的运动路程.
解:由题意,得
v(t)=
由变速直线运动的路程公式,可得:
s=v(t)dt=2tdt+2dt+(t+1)dt
=t2|+2t|+(t2+t)|=(m).
所以该物体在 s~6 s间的运动路程是 m.
11.求由曲线y=(x+2)2,x轴与直线y=4-x所围成的平面图形的面积.
解:
在同一坐标系内先画出曲线y=(x+2)2与直线y=4-x的图象(如图).
在方程y=(x+2)2中,令y=0,解得曲线与x轴的交点为A(-2,0).
同时,在y=4-x中,令y=0,解得直线与x轴的交点为B(4,0),再求得曲线y=(x+2)2与直线y=4-x的交点为C(0,4).
由图可以看出,所求图形的面积由S1与S2两部分(即图中的阴影部分)组成.
故所求的面积为:
S=S1+S2=(x+2)2dx+(4-x)dx
=(x+2)3|+(4x-x2)|=+8=.
12.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.
解:(1)设f(x)=ax2+bx+c(a≠0),
则f′(x)=2ax+b.
又f′(x)=2x+2,所以a=1,b=2.
∴f(x)=x2+2x+c.
又方程f(x)=0有两个相等实根,
即x2+2x+c=0有两个相等实根,
所以Δ=4-4c=0,即c=1.
故f(x)=x2+2x+1.
(2)依题意,所求面积为S=(x2+2x+1)dx,
取F(x)=x3+x2+x,则F′(x)=x2+2x+1,
∴S=(x2+2x+1)dx=F(0)-F(-1)=.
A.ln2 B.ln2-1
C.1+ln2 D.2ln2
解析:
选A.画出曲线y=(x>0)及直线x=1,x=2,y=0,则所求面积S为如图所示阴影部分面积.
∴S=dx=lnx|=ln2-ln1=ln2.故选A.
2.如果某质点以初速度v(0)=1,加速度a(t)=6t作直线运动,则质点在t=2 s时的瞬时速度为( )
A.5 B.7
C.9 D.13
解析:选D.v(2)-v(0)=a(t)dt=6tdt=3t2|,
∴v(2)=v(0)+3×22=1+12=13.
3.
(2010年高考陕西卷)从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为________.
解析:根据题意得:S阴=3x2dx=x3|=1,则点M取自阴影部分的概率为==.
答案:
4.一个弹簧压缩x cm可产生4x N的力,把它从自然长度压缩到比自然长度短5 cm,求弹簧克服弹力所做的功.
解:设F(x)=kx,因为弹簧压缩x cm可产生4x N的力,∴k=4.
∴弹簧克服弹力所做的功为
W=4xdx=4×(x2)|=50(J).
一、选择题
1.
如图,由曲线y=x2-1、直线x=0、x=2和x轴围成的封闭图形的面积是( )
A.(x2-1)dx
B.|(x2-1)dx|
C.|x2-1|dx
D.(x2-1)dx+(x2-1)dx
解析:选C.根据定积分的几何意义,结合面积是一个非负数求解.
2.
如图,阴影部分的面积为( )
A.f(x)dx
B.g(x)dx
C.[f(x)-g(x)]dx
D.[g(x)-f(x)]dx
解析:选C.由题图,易知在x∈[a,b]时,f(x)>g(x),
∴S=[f(x)-g(x)]dx.
3.求由y=ex,x=2,y=1围成的曲边梯形的面积时,若选择x为积分变量,则积分区间为( )
A.[0,e2] B.[0,2]
C.[1,2] D.[0,1]
解析:
选B.如图,作出y=ex,x=2,y=1三个函数的图象,由三者围成的曲边梯形如图阴影部分,若选择x为积分变量,则积分区间应为[0,2].故选B.
4.一物体在力F(x)=3x2-2x+5(力单位:N,位移单位:m)作用力下,沿与力F(x)相同的方向由x=5 m直线运动到x=10 m处做的功是( )
A.925 J B.850 J
C.825 J D.800 J
解析:选C.W=∫F(x)dx=∫(3x2-2x+5)dx
=(x3-x2+5x)|
=(1000-100+50)-(125-25+25)=825(J).
故选C.
5.一物体以速度v(t)=3t2-2t+3做直线运动,它在t=0和t=3这段时间内的位移是( )
A.9 B.18
C.27 D.36
解析:选C.s=v(t)dt=(3t2-2t+3)dt=(t3-t2+3t)|=33-32+3×3-0=27.故选C.
6.一物体在力F(x)=(单位:N)的作用下沿与力F相同的方向作直线运动,从x=0处运动到x=4(单位:m)处,则力F(x)作的功为( )
A.44 J B.46 J
C.48 J D.50 J
解析:选B.W=F(x)dx=10dx+(3x+4)dx=10x|+(x2+4x)|=46(J).故选B.
二、填空题
7.若1 N的力能使弹簧伸长2 cm,则使弹簧伸长12 cm时克服弹力所作的功为________.
解析:弹簧的伸长与所受到的拉力成正比,设F=kx,求得k=50,∴F(x)=50x.
∴W=∫50xdx=25x2|=0.36(J).
答案:0.36 J
8.有一横截面的面积为4 cm2的水管控制往外流水,打开水管后t秒末的流速为v(t)=6t-t2(单位:cm/s)(0≤t≤6).则t=0到t=6这段时间内流出的水量为________.
解析:由题意可得t=0到t=6这段时间内流出的水量V=4(6t-t2)dt=4(6t-t2)dt=4(3t2-t3)|=144(cm3).故t=0到t=6这段时间内流出的水量为144 cm3.
答案:144 cm3
9.由曲线y=x2+4与直线y=5x,x=0,x=4所围成平面图形的面积是________.
解析:
由得x=1或x=4.
所求面积为S=(x2+4-5x)dx+(5x-x2-4)dx
=(x3+4x-x2)|+(x2-x3-4x)|=.
答案:
三、解答题
10.
一物体做变速直线运动,其v-t曲线如图所示,求该物体在 s~6 s间的运动路程.
解:由题意,得
v(t)=
由变速直线运动的路程公式,可得:
s=v(t)dt=2tdt+2dt+(t+1)dt
=t2|+2t|+(t2+t)|=(m).
所以该物体在 s~6 s间的运动路程是 m.
11.求由曲线y=(x+2)2,x轴与直线y=4-x所围成的平面图形的面积.
解:
在同一坐标系内先画出曲线y=(x+2)2与直线y=4-x的图象(如图).
在方程y=(x+2)2中,令y=0,解得曲线与x轴的交点为A(-2,0).
同时,在y=4-x中,令y=0,解得直线与x轴的交点为B(4,0),再求得曲线y=(x+2)2与直线y=4-x的交点为C(0,4).
由图可以看出,所求图形的面积由S1与S2两部分(即图中的阴影部分)组成.
故所求的面积为:
S=S1+S2=(x+2)2dx+(4-x)dx
=(x+2)3|+(4x-x2)|=+8=.
12.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.
解:(1)设f(x)=ax2+bx+c(a≠0),
则f′(x)=2ax+b.
又f′(x)=2x+2,所以a=1,b=2.
∴f(x)=x2+2x+c.
又方程f(x)=0有两个相等实根,
即x2+2x+c=0有两个相等实根,
所以Δ=4-4c=0,即c=1.
故f(x)=x2+2x+1.
(2)依题意,所求面积为S=(x2+2x+1)dx,
取F(x)=x3+x2+x,则F′(x)=x2+2x+1,
∴S=(x2+2x+1)dx=F(0)-F(-1)=.
