常用逻辑用语 课件(新课标A版)
文档属性
| 名称 | 常用逻辑用语 课件(新课标A版) |

|
|
| 格式 | zip | ||
| 文件大小 | 448.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-09 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
常用逻辑用语
1.命题的概念
在数学中用语言、符号或式子表达的,可以 的陈述句叫做命题.其中 的语句叫真命题,
的语句叫假命题.
2.四种命题及其关系
(1)四种命题
判断真假
判断为真
判断为假
命 题 表述形式
原命题
若p,则q
逆命题
否命题
逆否命题
若q ,则 p
若 p,则 q
若 q,则 p
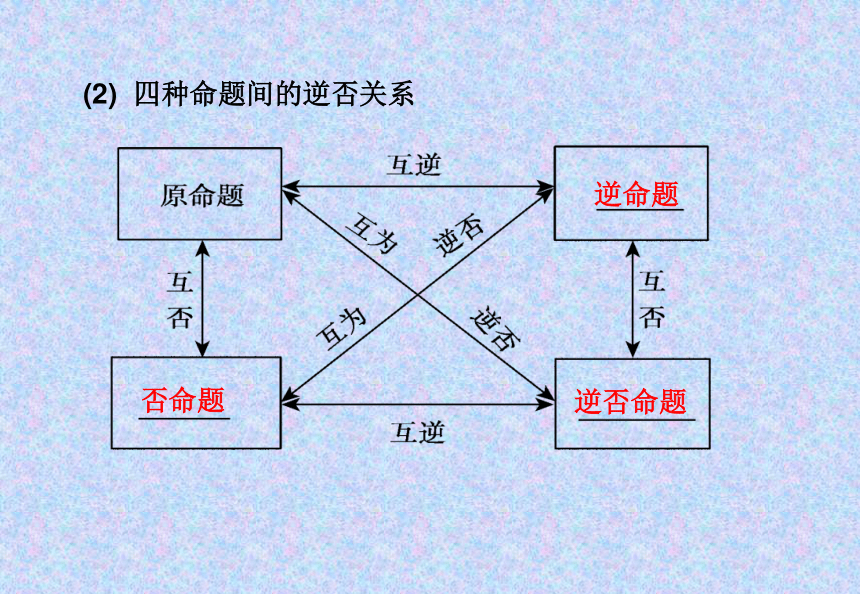
(2) 四种命题间的逆否关系
逆命题
否命题
逆否命题
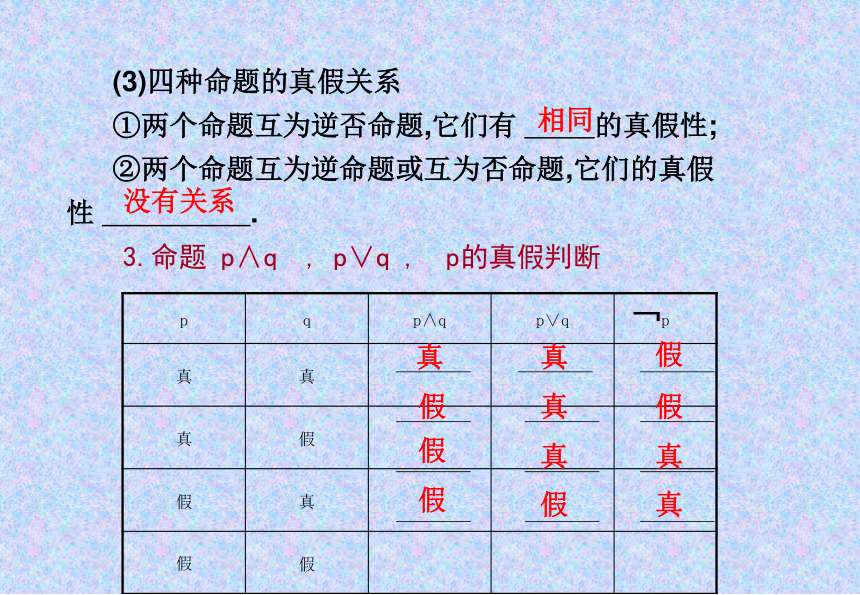
(3)四种命题的真假关系
①两个命题互为逆否命题,它们有 的真假性;
②两个命题互为逆命题或互为否命题,它们的真假
性 .
3.命题 p∧q , p∨q ,?p的真假判断
相同
没有关系
p q p∧q p∨q p
真 真
真 假
假 真
假 假
真
真
真
真
真
真
假
假
假
假
假
假
4.含有一个量词的命题的否定
?
5.充分条件与必要条件
(1)如果p? q,则p是q的 ,q是p ;
(2)如果p? q,q ?p,则p是q的 .
6.特别注意:命题的否命题是既否定命题的条件,又否
定命题的结论;而命题的否定是只否定命题的结论.
命 题 命题的否定
?x∈M,P(x)
x∈M,P(x)
充要条件
充分条件
必要条件
x∈M,? P(x)
x∈M,? P(x)
考点一 判断含有逻辑联结词的命题的真假
分别写出由下列各组命题构成的“p∨q”“p∧q”“ p”形式的命题的真假.
(1) p:3是9的约数,q:3是18的约数;
(2) p:菱形的对角线相等,q :菱形的对角线互相垂直;
(3) p:方程x2+x-1=0的两实根符号相同, q : 方程x2+x-
1=0的两实根绝对值相等;
(4) p:π是有理数,q:π是无理数.
【分析】由含逻辑联结词 “或” “且” “非” 的命
题的形式及其真值表直接判断.
【解析】 (1) ∵p是真命题,q是真命题,
∴p∨q是真命题,p∧q是真命题, p是假命题.
(2) ∵p是假命题,q是真命题,
∴p∨q是真命题,p∧q是假命题, p是真命题.
(3) ∵p是假命题,q是假命题,
∴p∨q是假命题,p∧q是假命题, p是真命题.
(4) ∵p是假命题,q是真命题,
∴p∨q是真命题,p∧q是假命题, p是真命题.
【评析】判断含有逻辑联结词“或”“且”“非”的命题的真假:①必须弄清构成它的命题的真假;②弄清结构形式;③由真值表判断真假.
分别指出由下列命题构成的“p∨q”“p∧q”“ p”形式的命题的真假.
(1) p:4∈{2,3},q:2∈{2,3};
(2) p:1是奇数,q:1 是质数;
(3) p:0∈?,q:{x|x2-3x-5<0}?R;
(4) p:5≤5,q:27不是质数.
*对应演练*
(1) ∵p是假命题,q是真命题,
∴p∨q为真命题 , p∧q为假命题, p为真命题.
(2) ∵1是奇数,∴p是真命题,
又∵1不是质数,∴q是假命题,
因此p∨q为真命题,p∧q为假命题, p为假命题.
(3) ∵0?? ,∴p为假命题,
又∵x2-3x-5<0?
∴{x|x2-3x-5<0}
= 成立.∴q为真命题.
∴p∨q为真命题, p∧q为假命题, p为真命题.
(4)显然p:5≤5为真命题,q: 27不是质数为真命题,
∴p∨q为真命题,p∧q为真命题, p为假命题.
考点二 判断命题的“否定”的真假
写出下列命题的否定,并判断其真假.
p:?x∈R,
q:所有的正方形都是矩形;
(3) r:?x∈R,x2+2x+2≤0;
(4)s:至少有一个实数x,使x3+1=0.
【分析】在全称命题和特称命题的否定中,应明确全称量词与存在量词是如何对应转换的, 全称命题的否定是特称命题,而特称命题的否定是全称命题.
【解析】 (1) p:?x∈R, x2-x+ <0.(假)
这是由于?x∈R, x2-x+ =(x- )2≥0恒成立.
(2) q:至少存在一个正方形不是矩形.(假)
(3) r: x∈R,x2+2x+2>0.(真)
(4) s: x∈R,x3+1≠0.(假)
【评析】命题的“否定”与一个命题的“否命题”是两个不同的概念,对命题 p 的否定是否定命题所作的判断, 而“否命题”是对“若p,则q”形式的命题而言,既要否定条件也要否定结论.
*对应演练*
写出下列命题的否定,并判定真假.
(1) 所有的矩形都是平行四边形;
(2) 有些实数的绝对值是正数.
(1) 至少存在一个矩形不是平行四边形(假).
(2) 所有实数的绝对值都是正数(假).
考点三 四种命题及真假的判断
把下列命题改写成“若p ,则 q”的形式 ,并写出它们
的 逆命题、否命题、逆否命题.
(1)正三角形的三内角相等;
(2)全等三角形的面积相等;
(3)已知a,b,c,d是实数,若a=b,c=d,则a+c=b+d.
【分析】 先找出原命题的条件p和结论q , 然后根
据四种命题之间的关系直接写出.
【解析】 (1) 原命题 : 若一个三角形是正三角形, 则 它的三个内角相等.
逆命题:若一个三角形的三个内角相等,则这个三角形是正三角形(或写成 : 三个内角相等的三角形是正三角形).
否命题:若一个三角形不是正三角形,则它的三个内角不全相等.
逆否命题:若一个三角形的三个内角不全相等,那么这个三角形不是正三角形 (或写成 :三个内角不全相等的三角形不是正三角形).
(2)原命题:若两个三角形全等 , 则它们的面积相等.
逆命题:若两个三角形面积相等,则这两个三角形全等(或写成:面积相等的三角形全等).
否命题:若两个三角形不全等,则这两个三角形面积不相等(或写成:不全等的三角形面积不相等).
逆否命题:若两个三角形面积不相等, 则这两个三角形不全等.
(3)原命题:已知a,b,c,d是实数,若a=b,c=d,则a+c=b+d.其中“已知a,b,c,d是实数”是大前提, “a与b, c与d都相等”是条件p,“a+c=b+d”是结论q,所以
逆命题:已知a,b,c,d是实数,若a+c=b+d , 则a 与b,c与d都相等.
否命题:已知a,b,c,d是实数,若a与b,c与d不都相等,则a+c≠b+d.
逆否命题:已知a,b,c,d是实数,若a+c≠b+d,则a与b, c与d不都相等.
【评析】已知原命题,写出它的其他三种命题,首先把原命题改写成“若p,则q”的形式,然后找出其条件p和结论q,再根据四种命题的定义写出其他命题.
逆命题:“若q,则p”;否命题:“若 p,则 q”;
逆否命题:“若 q,则 p”,对写出的命题也可简洁表述;对于含有大前提的命题,在改写命题形式时,大前提不要动.
把下列命题写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题,并判断其真假.
(1)当x=2时,x2-3x+2=0;
(2)对顶角相等.
*对应演练*
返回目录
(1)原命题:若x=2,则x2-3x+2=0.为真命题.
逆命题:若x2-3x+2=0,则x=2.为假命题.
否命题:若x≠2,则x2-3x+2≠0.为假命题.
逆否命题:若x2-3x+2≠0,则x≠2.为真命题.
(2)原命题:若两个角是对顶角,则它们相等.为真命题.
逆命题:若两个角相等,则它们是对顶角.为假命题.
否命题:若两个角不是对顶角,则它们不相等.为假命题.
逆否命题:若两个角不相等,则它们不是对顶角.为真命题.
考点四 充要条件的判断
给出下列命题:
①p:x-2=0;q:(x-2)(x-3)=0;
②p:两个三角形相似;q:两个三角形全等;
③p:m<-2;q:方程x2-x-m=0无实根;
④p:一个四边形是矩形;q:四边形的对角线相等.
试分别指出p是q的什么条件.
【分析】 (1)首先分清条件和结论.(2)再看条件
能否推出结论,结论能否推出条件.
【解析】①∵x-2=0?(x-2)(x-3)=0,
而(x-2)(x-3)=0?/ x-2=0,
∴p是q的充分不必要条件.
②∵两个三角形相似?/ 两个三角形全等,
但两个三角形全等? 两个三角形相似,
∴p是q的必要不充分条件.
③∵m<-2?方程x2-x-m=0无实根,
方程x2-x-m=0无实根?/ m<-2,
∴p是q的充分不必要条件.
④∵矩形的对角线相等,∴p q,
而对角线相等的四边形不一定是矩形,
∴q / p,∴p是q的充分不必要条件.
【评析】 (1)判断p 是q 的什么条件 , 关键是看p能否推出q,q能否推出p.
(2)若“p? q” 是否成立,不能判断或不好处理 ,则可看它的逆否命题是否成立.
(3)否定一个结论时,只需举一个反例即可.
*对应演练*
指出下列命题中,p是q的什么条件(在“充分不必要条件”
“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答).
(1)在△ABC中, p:∠A=∠B,q:sinA=sinB;
(2)对于实数x,y, p:x+y≠8,q:x≠2或y≠6;
(3)非空集合A,B中, p:x∈A∪B,q:x∈B;
(4)已知x,y∈R, p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
(2)易知, p:x+y=8, q:x=2且y=6,显然 q? p, 但
p / q,即 q是 p的充分不必要条件,根据原命题和逆否命题的等价性知,p是q的充分不必要条件.
(3)显然x∈A∪B不一定有x∈B,但x∈B一定有x∈A∪B,所以p是q的必要不充分条件.
(4)条件p:x=1且y=2,条件q:x=1或y=2,
所以p? q但q / p,故p是q的充分不必要条件.
(1)在△ABC中,∠A=∠B sinA=sinB,反之,若sinA=
sinB,因为A与B不可能互补(因为三角形三个内角和为180°),所以只有A=B.故p是q的充要条件.
考点五 充要条件的证明
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0.
【分析】 此类问题需证明两个命题,即充分性与必要性,故应分清谁是条件,谁是结论,然后再分别证明.
【证明】 (必要性)
∵a+b=1,∴a+b-1=0,∴a3+b3+ab-a2-b2
=(a+b)(a2-ab+b2)-(a2-ab+b2)=(a+b-1)(a2-ab+b2)=0.
(充分性)
∵a3+b3+ab-a2-b2=0, 即(a+b-1)(a2-ab+b2)=0,
又ab≠0,∴a≠0且b≠0,
∴a2-ab+b2=(a- )2+ >0,
∴a+b-1=0,即a+b=1.
综上可知,当ab≠0时,a+b=1的充要条件是a3+b3+ab- a2
-b2=0.
【评析】有关充要条件的证明问题,要分清哪个是条件,哪个是结论,由“条件”? “结论”是证明命题的充分性,由“结论”?“条件”是证明命题的必要性. 证明要分两个环节:一是充分性;二是必要性.
*对应演练*
证明一元二次方程ax2 + bx +c=0有一正根和一负根的充
要条件是ac<0.
证明:充分性:若ac<0,则b2-4ac>0,且ca<0,
∴方程ax2+bx+c=0有两个相异实根, 且两根异号, 即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则Δ=b2-4ac>0,x1x2=ca<0,∴ac<0.
综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
考点六 利用复合命题的真假求参数的值或范围
已知p:方程x2+mx+1=0有两个不等的负根;q : 方程4x2+4(m-2)x+1=0无实根 .若 p或q为真,p 且 q为假,
求m的取值范围.
【分析】(1)“p∧q”为假,包括“p真q假”“p假q真”
“p假q假”;
(2)“p∨q”为假,则“p假q假”;
(3)“ p”为假,则“p真”.
【解析】若方程x2+mx+1=0有两个不等的负根,则
Δ=m2- 4>0
m>0,
若方程4x2+4(m-2)x+1=0无实根,
则Δ=16(m-2)2-16=16(m2-4m+3)<0,
解得1因为p或q为真,所以p,q至少有一个为真.
又p且q为假,所以p,q至少有一个为假.
因此,p,q两命题应一真一假,
即p为真,q为假或p为假,q为真.
m>2 m≤2
m≤1或m≥3 1解得m>2,即p:m>2.
或
所以
【评析】 (1)由简单命题和逻辑联结词构成的复合命题的真假可以用真值表来判断,反之根据复合命题的真假也可以判断简单命题的真假.假若p且q真,则p 真,q也真;若p或q真,则p,q至少有一个真;若p且q假,则p,q至少有一个假.
(2)可把“p或q”为真命题转化为并集的运算;把“p且q”为真命题转化为交集的运算.
由 ,得 ≤0,即 ≤0,得0≤m< 3 ,
∴p:? m∈R,0≤m<3.
由关于x的不等式x2-4x+m2≤0的解集是空集得Δ=16-4m2<0, ∴m>2或m<-2,∴q:?m∈R,m>2或m<-2,
*对应演练*
(2011年唐山一模)设p: ;q:关于x的不等式x2-4x+m2≤0 的解集是空集,若“p∨q”为真命题,“p∧q”为假命题,求m的取值范围.
∵p∨q为真,p∧q为假,
∴p,q有且只有一个为真.
①若p真q假,则0≤m<3且-2≤m≤2,
∴0≤m≤2.
②若p假q真,则m<0或m≥3,同时m<-2或m>2,
∴m<-2或m≥3.
∴m的取值范围是(-∞,-2)∪[0,2]∪[3,+∞).
1.命题的否定与否命题是完全不同的概念
(1) 任何命题均有否定 ,无论是真命题还是假命题 ;而否命题仅针对命题“若p,则q”提出来的.
(2)命题的否定是原命题的矛盾命题,两者的真假性必然是一真一假 ;而否命题与原命题可能是同真同 假,也可能是一真一假.
2.一个命题的原命题与其逆否命题同真假;原命题的逆命题与否命题互为逆否关系,也同真假.有时一个命题的真假不易被判断时, 可以通过判断它的逆否命题的真假,从而得知原命题的真假.
3.“p∨q”为真,当且仅当p和q中至少一个为真(一真为真);“p∧q”为假,当且仅当p和q中至少一个为假(一假为假);p与 p真假相反.
4.A是B的充分不必要条件是指:A?B 且 B / A;
5.A的充分不必要条件是B,是指:B?A且 A / B.这两种说法是在充分必要条件推理判断中经常出现且容易混淆的说法 ,在解题中一定要根据问题的设问方式 ,弄清它们的区别,以免出现判断错误.
常用逻辑用语
1.命题的概念
在数学中用语言、符号或式子表达的,可以 的陈述句叫做命题.其中 的语句叫真命题,
的语句叫假命题.
2.四种命题及其关系
(1)四种命题
判断真假
判断为真
判断为假
命 题 表述形式
原命题
若p,则q
逆命题
否命题
逆否命题
若q ,则 p
若 p,则 q
若 q,则 p
(2) 四种命题间的逆否关系
逆命题
否命题
逆否命题
(3)四种命题的真假关系
①两个命题互为逆否命题,它们有 的真假性;
②两个命题互为逆命题或互为否命题,它们的真假
性 .
3.命题 p∧q , p∨q ,?p的真假判断
相同
没有关系
p q p∧q p∨q p
真 真
真 假
假 真
假 假
真
真
真
真
真
真
假
假
假
假
假
假
4.含有一个量词的命题的否定
?
5.充分条件与必要条件
(1)如果p? q,则p是q的 ,q是p ;
(2)如果p? q,q ?p,则p是q的 .
6.特别注意:命题的否命题是既否定命题的条件,又否
定命题的结论;而命题的否定是只否定命题的结论.
命 题 命题的否定
?x∈M,P(x)
x∈M,P(x)
充要条件
充分条件
必要条件
x∈M,? P(x)
x∈M,? P(x)
考点一 判断含有逻辑联结词的命题的真假
分别写出由下列各组命题构成的“p∨q”“p∧q”“ p”形式的命题的真假.
(1) p:3是9的约数,q:3是18的约数;
(2) p:菱形的对角线相等,q :菱形的对角线互相垂直;
(3) p:方程x2+x-1=0的两实根符号相同, q : 方程x2+x-
1=0的两实根绝对值相等;
(4) p:π是有理数,q:π是无理数.
【分析】由含逻辑联结词 “或” “且” “非” 的命
题的形式及其真值表直接判断.
【解析】 (1) ∵p是真命题,q是真命题,
∴p∨q是真命题,p∧q是真命题, p是假命题.
(2) ∵p是假命题,q是真命题,
∴p∨q是真命题,p∧q是假命题, p是真命题.
(3) ∵p是假命题,q是假命题,
∴p∨q是假命题,p∧q是假命题, p是真命题.
(4) ∵p是假命题,q是真命题,
∴p∨q是真命题,p∧q是假命题, p是真命题.
【评析】判断含有逻辑联结词“或”“且”“非”的命题的真假:①必须弄清构成它的命题的真假;②弄清结构形式;③由真值表判断真假.
分别指出由下列命题构成的“p∨q”“p∧q”“ p”形式的命题的真假.
(1) p:4∈{2,3},q:2∈{2,3};
(2) p:1是奇数,q:1 是质数;
(3) p:0∈?,q:{x|x2-3x-5<0}?R;
(4) p:5≤5,q:27不是质数.
*对应演练*
(1) ∵p是假命题,q是真命题,
∴p∨q为真命题 , p∧q为假命题, p为真命题.
(2) ∵1是奇数,∴p是真命题,
又∵1不是质数,∴q是假命题,
因此p∨q为真命题,p∧q为假命题, p为假命题.
(3) ∵0?? ,∴p为假命题,
又∵x2-3x-5<0?
∴{x|x2-3x-5<0}
= 成立.∴q为真命题.
∴p∨q为真命题, p∧q为假命题, p为真命题.
(4)显然p:5≤5为真命题,q: 27不是质数为真命题,
∴p∨q为真命题,p∧q为真命题, p为假命题.
考点二 判断命题的“否定”的真假
写出下列命题的否定,并判断其真假.
p:?x∈R,
q:所有的正方形都是矩形;
(3) r:?x∈R,x2+2x+2≤0;
(4)s:至少有一个实数x,使x3+1=0.
【分析】在全称命题和特称命题的否定中,应明确全称量词与存在量词是如何对应转换的, 全称命题的否定是特称命题,而特称命题的否定是全称命题.
【解析】 (1) p:?x∈R, x2-x+ <0.(假)
这是由于?x∈R, x2-x+ =(x- )2≥0恒成立.
(2) q:至少存在一个正方形不是矩形.(假)
(3) r: x∈R,x2+2x+2>0.(真)
(4) s: x∈R,x3+1≠0.(假)
【评析】命题的“否定”与一个命题的“否命题”是两个不同的概念,对命题 p 的否定是否定命题所作的判断, 而“否命题”是对“若p,则q”形式的命题而言,既要否定条件也要否定结论.
*对应演练*
写出下列命题的否定,并判定真假.
(1) 所有的矩形都是平行四边形;
(2) 有些实数的绝对值是正数.
(1) 至少存在一个矩形不是平行四边形(假).
(2) 所有实数的绝对值都是正数(假).
考点三 四种命题及真假的判断
把下列命题改写成“若p ,则 q”的形式 ,并写出它们
的 逆命题、否命题、逆否命题.
(1)正三角形的三内角相等;
(2)全等三角形的面积相等;
(3)已知a,b,c,d是实数,若a=b,c=d,则a+c=b+d.
【分析】 先找出原命题的条件p和结论q , 然后根
据四种命题之间的关系直接写出.
【解析】 (1) 原命题 : 若一个三角形是正三角形, 则 它的三个内角相等.
逆命题:若一个三角形的三个内角相等,则这个三角形是正三角形(或写成 : 三个内角相等的三角形是正三角形).
否命题:若一个三角形不是正三角形,则它的三个内角不全相等.
逆否命题:若一个三角形的三个内角不全相等,那么这个三角形不是正三角形 (或写成 :三个内角不全相等的三角形不是正三角形).
(2)原命题:若两个三角形全等 , 则它们的面积相等.
逆命题:若两个三角形面积相等,则这两个三角形全等(或写成:面积相等的三角形全等).
否命题:若两个三角形不全等,则这两个三角形面积不相等(或写成:不全等的三角形面积不相等).
逆否命题:若两个三角形面积不相等, 则这两个三角形不全等.
(3)原命题:已知a,b,c,d是实数,若a=b,c=d,则a+c=b+d.其中“已知a,b,c,d是实数”是大前提, “a与b, c与d都相等”是条件p,“a+c=b+d”是结论q,所以
逆命题:已知a,b,c,d是实数,若a+c=b+d , 则a 与b,c与d都相等.
否命题:已知a,b,c,d是实数,若a与b,c与d不都相等,则a+c≠b+d.
逆否命题:已知a,b,c,d是实数,若a+c≠b+d,则a与b, c与d不都相等.
【评析】已知原命题,写出它的其他三种命题,首先把原命题改写成“若p,则q”的形式,然后找出其条件p和结论q,再根据四种命题的定义写出其他命题.
逆命题:“若q,则p”;否命题:“若 p,则 q”;
逆否命题:“若 q,则 p”,对写出的命题也可简洁表述;对于含有大前提的命题,在改写命题形式时,大前提不要动.
把下列命题写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题,并判断其真假.
(1)当x=2时,x2-3x+2=0;
(2)对顶角相等.
*对应演练*
返回目录
(1)原命题:若x=2,则x2-3x+2=0.为真命题.
逆命题:若x2-3x+2=0,则x=2.为假命题.
否命题:若x≠2,则x2-3x+2≠0.为假命题.
逆否命题:若x2-3x+2≠0,则x≠2.为真命题.
(2)原命题:若两个角是对顶角,则它们相等.为真命题.
逆命题:若两个角相等,则它们是对顶角.为假命题.
否命题:若两个角不是对顶角,则它们不相等.为假命题.
逆否命题:若两个角不相等,则它们不是对顶角.为真命题.
考点四 充要条件的判断
给出下列命题:
①p:x-2=0;q:(x-2)(x-3)=0;
②p:两个三角形相似;q:两个三角形全等;
③p:m<-2;q:方程x2-x-m=0无实根;
④p:一个四边形是矩形;q:四边形的对角线相等.
试分别指出p是q的什么条件.
【分析】 (1)首先分清条件和结论.(2)再看条件
能否推出结论,结论能否推出条件.
【解析】①∵x-2=0?(x-2)(x-3)=0,
而(x-2)(x-3)=0?/ x-2=0,
∴p是q的充分不必要条件.
②∵两个三角形相似?/ 两个三角形全等,
但两个三角形全等? 两个三角形相似,
∴p是q的必要不充分条件.
③∵m<-2?方程x2-x-m=0无实根,
方程x2-x-m=0无实根?/ m<-2,
∴p是q的充分不必要条件.
④∵矩形的对角线相等,∴p q,
而对角线相等的四边形不一定是矩形,
∴q / p,∴p是q的充分不必要条件.
【评析】 (1)判断p 是q 的什么条件 , 关键是看p能否推出q,q能否推出p.
(2)若“p? q” 是否成立,不能判断或不好处理 ,则可看它的逆否命题是否成立.
(3)否定一个结论时,只需举一个反例即可.
*对应演练*
指出下列命题中,p是q的什么条件(在“充分不必要条件”
“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答).
(1)在△ABC中, p:∠A=∠B,q:sinA=sinB;
(2)对于实数x,y, p:x+y≠8,q:x≠2或y≠6;
(3)非空集合A,B中, p:x∈A∪B,q:x∈B;
(4)已知x,y∈R, p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
(2)易知, p:x+y=8, q:x=2且y=6,显然 q? p, 但
p / q,即 q是 p的充分不必要条件,根据原命题和逆否命题的等价性知,p是q的充分不必要条件.
(3)显然x∈A∪B不一定有x∈B,但x∈B一定有x∈A∪B,所以p是q的必要不充分条件.
(4)条件p:x=1且y=2,条件q:x=1或y=2,
所以p? q但q / p,故p是q的充分不必要条件.
(1)在△ABC中,∠A=∠B sinA=sinB,反之,若sinA=
sinB,因为A与B不可能互补(因为三角形三个内角和为180°),所以只有A=B.故p是q的充要条件.
考点五 充要条件的证明
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0.
【分析】 此类问题需证明两个命题,即充分性与必要性,故应分清谁是条件,谁是结论,然后再分别证明.
【证明】 (必要性)
∵a+b=1,∴a+b-1=0,∴a3+b3+ab-a2-b2
=(a+b)(a2-ab+b2)-(a2-ab+b2)=(a+b-1)(a2-ab+b2)=0.
(充分性)
∵a3+b3+ab-a2-b2=0, 即(a+b-1)(a2-ab+b2)=0,
又ab≠0,∴a≠0且b≠0,
∴a2-ab+b2=(a- )2+ >0,
∴a+b-1=0,即a+b=1.
综上可知,当ab≠0时,a+b=1的充要条件是a3+b3+ab- a2
-b2=0.
【评析】有关充要条件的证明问题,要分清哪个是条件,哪个是结论,由“条件”? “结论”是证明命题的充分性,由“结论”?“条件”是证明命题的必要性. 证明要分两个环节:一是充分性;二是必要性.
*对应演练*
证明一元二次方程ax2 + bx +c=0有一正根和一负根的充
要条件是ac<0.
证明:充分性:若ac<0,则b2-4ac>0,且ca<0,
∴方程ax2+bx+c=0有两个相异实根, 且两根异号, 即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则Δ=b2-4ac>0,x1x2=ca<0,∴ac<0.
综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
考点六 利用复合命题的真假求参数的值或范围
已知p:方程x2+mx+1=0有两个不等的负根;q : 方程4x2+4(m-2)x+1=0无实根 .若 p或q为真,p 且 q为假,
求m的取值范围.
【分析】(1)“p∧q”为假,包括“p真q假”“p假q真”
“p假q假”;
(2)“p∨q”为假,则“p假q假”;
(3)“ p”为假,则“p真”.
【解析】若方程x2+mx+1=0有两个不等的负根,则
Δ=m2- 4>0
m>0,
若方程4x2+4(m-2)x+1=0无实根,
则Δ=16(m-2)2-16=16(m2-4m+3)<0,
解得1
又p且q为假,所以p,q至少有一个为假.
因此,p,q两命题应一真一假,
即p为真,q为假或p为假,q为真.
m>2 m≤2
m≤1或m≥3 1
或
所以
【评析】 (1)由简单命题和逻辑联结词构成的复合命题的真假可以用真值表来判断,反之根据复合命题的真假也可以判断简单命题的真假.假若p且q真,则p 真,q也真;若p或q真,则p,q至少有一个真;若p且q假,则p,q至少有一个假.
(2)可把“p或q”为真命题转化为并集的运算;把“p且q”为真命题转化为交集的运算.
由 ,得 ≤0,即 ≤0,得0≤m< 3 ,
∴p:? m∈R,0≤m<3.
由关于x的不等式x2-4x+m2≤0的解集是空集得Δ=16-4m2<0, ∴m>2或m<-2,∴q:?m∈R,m>2或m<-2,
*对应演练*
(2011年唐山一模)设p: ;q:关于x的不等式x2-4x+m2≤0 的解集是空集,若“p∨q”为真命题,“p∧q”为假命题,求m的取值范围.
∵p∨q为真,p∧q为假,
∴p,q有且只有一个为真.
①若p真q假,则0≤m<3且-2≤m≤2,
∴0≤m≤2.
②若p假q真,则m<0或m≥3,同时m<-2或m>2,
∴m<-2或m≥3.
∴m的取值范围是(-∞,-2)∪[0,2]∪[3,+∞).
1.命题的否定与否命题是完全不同的概念
(1) 任何命题均有否定 ,无论是真命题还是假命题 ;而否命题仅针对命题“若p,则q”提出来的.
(2)命题的否定是原命题的矛盾命题,两者的真假性必然是一真一假 ;而否命题与原命题可能是同真同 假,也可能是一真一假.
2.一个命题的原命题与其逆否命题同真假;原命题的逆命题与否命题互为逆否关系,也同真假.有时一个命题的真假不易被判断时, 可以通过判断它的逆否命题的真假,从而得知原命题的真假.
3.“p∨q”为真,当且仅当p和q中至少一个为真(一真为真);“p∧q”为假,当且仅当p和q中至少一个为假(一假为假);p与 p真假相反.
4.A是B的充分不必要条件是指:A?B 且 B / A;
5.A的充分不必要条件是B,是指:B?A且 A / B.这两种说法是在充分必要条件推理判断中经常出现且容易混淆的说法 ,在解题中一定要根据问题的设问方式 ,弄清它们的区别,以免出现判断错误.
