北京四中2011~2012学年度第二学期期中检测初二年级数学学科及答案
文档属性
| 名称 | 北京四中2011~2012学年度第二学期期中检测初二年级数学学科及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-09 00:00:00 | ||
图片预览




文档简介
北京四中2011~2012学年度第二学期期中检测初二年级数学学科 第 1 页 共6页
数 学 试 卷
(考试时间为100分钟,试卷满分为100分)
班级 学号 姓名 分数
一.选择题(本题共30分,每小题3分)
1.对于函数,若时,,则这个函数的解析式是( )
A. B. C. D.
2.下列各式中,运算正确的是( )
A. B.
C. ( http: / / www. / ) D.
3.下列说法中正确的是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相垂直且相等的四边形是正方形
D.两条对角线互相平分的四边形是平行四边形
4. 图象上有两点A(x1,y1)和 B(x2,y2),若y1A.0 < x1 < x2 B.0 > x1 > x2 C.x1 < x2 < 0 D.x1 > x2> 0
5. 如图,□ABCD中,∠DAB的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
A.1 B.1.5 C.2 D.3
6. 若一个等腰梯形的周长为30cm,腰长为6cm, 则它的中位线长为( )
A. 12cm B. 6cm C. 18cm D. 9cm
7.下列三角形中,不是直角三角形的是( )
A.三个内角之比为5∶6∶1 B. 一边上的中线等于这一边的一半
C.三边之长为20、21、29 D. 三边之比为1.5 : 2 : 3
8.如图,数轴上点A所表示的数为a,则a的值是( )
A.-1 B.-+1 C.+1 D.
9.如图,菱形ABCD中,E、F分别是AB、AC的中点,
若EF=3,则菱形ABCD的周长是( )
A.12 B.16
C.20 D.24
10.如图,矩形AOBC中,点A的坐标为(0,8),点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
30 B.32 C.34 D.16
二.填空题(本题共16分,每小题2分)
11.函数y =中自变量x的取值范围是_______.
12.在□ABCD中,∠A=70°,∠D=________ .
13. 比较大小: .
14.若是关于的方程的一个根,则_______.
15.矩形的两条对角线所夹的锐角为60,较短的边长为12,则对角线长为_______.
16.顺次连接等腰梯形各边中点得到的四边形是_________________.
17.如图,如果曲线l1是反比例函数在第一象限内的图象,且过点A (2,1), 那么与l1关于x轴对称的曲线l2的解析式为 (x>0).
18.如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边做垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为__________.
三.计算(本题共20分,第19题12分,第20题8分)
19.计算:
(1) (2)
解:原式= 解:原式=
(3)
解:原式=
20.解关于x的方程
(1); (2)(其中k为常数).
解: 解:
四.解答题(本题共22分,第21,22题6分,第23,24题每题5分)
21. 在□ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
22.甲乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时.问二人每小时各走几千米?
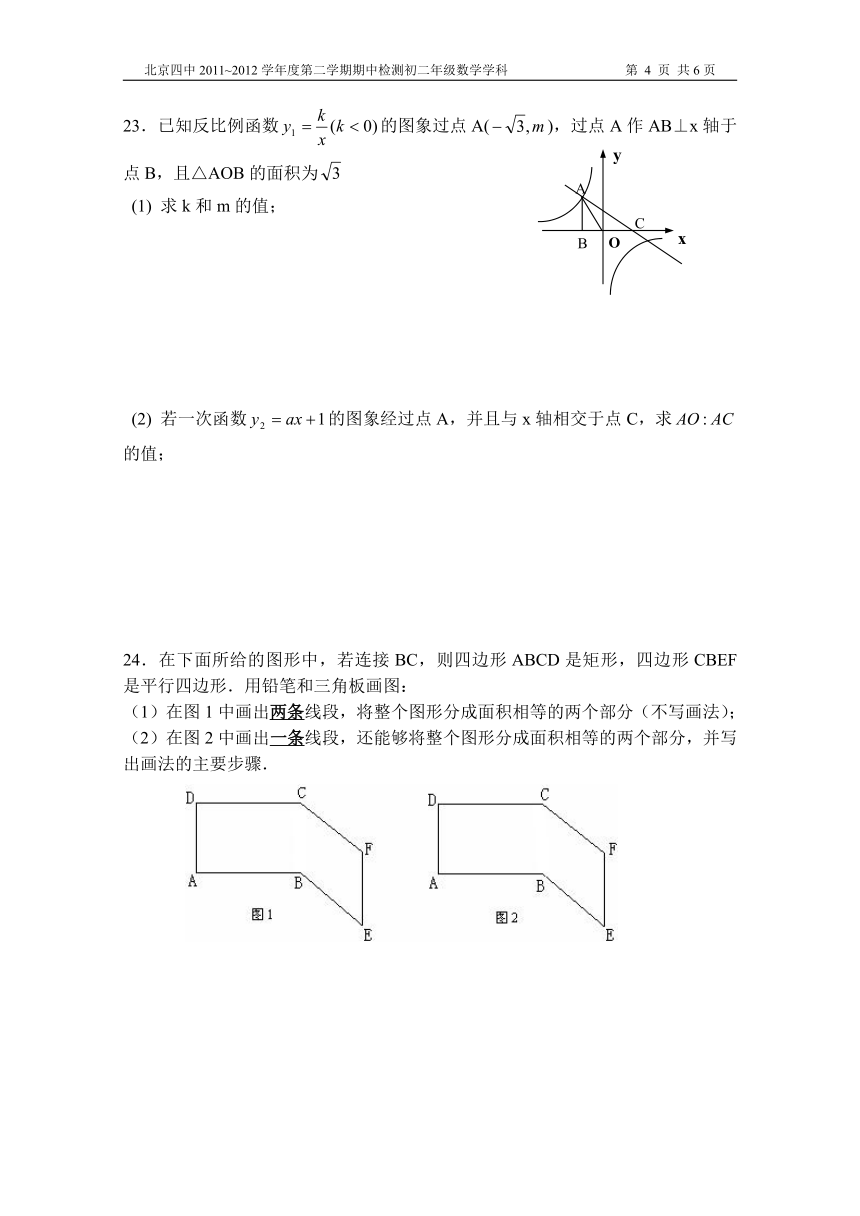
23.已知反比例函数的图象过点A(),过点A作AB⊥x轴于点B,且△AOB的面积为
(1) 求k和m的值;
(2) 若一次函数的图象经过点A,并且与x轴相交于点C,求的值;
24.在下面所给的图形中,若连接BC,则四边形ABCD是矩形,四边形CBEF是平行四边形.用铅笔和三角板画图:
(1)在图1中画出两条线段,将整个图形分成面积相等的两个部分(不写画法);
(2)在图2中画出一条线段,还能够将整个图形分成面积相等的两个部分,并写出画法的主要步骤.
五.解答题(本题共12分,第25、26题每题6分)
25. 有一块直角三角形纸片, 两直角边AC = 6cm, BC = 8cm,
①如图1,现将纸片沿直线AD折叠, 使直角边AC落在斜边AB上, 且与AB重合, 则CD = _________.
图1 图2
② 如图2,若将直角∠C沿MN折叠, 使点C落在AB中点H上, 点M、N分别在AC、BC上, 则、与之间有怎样的数量关系?并证明你的结论。
26. 如图1,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF.
(1)若四边形ABCD为正方形,当∠EAF=45°时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
(2)如图2,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明.
(3)在(2)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).
图1 图2
数 学 试 卷 参 考 答 案
一.选择题(本题共30分,每小题3分)
1 2 3 4 5 6 7 8 9 10
C C D A C D D A D A
二.填空题(本题共16分,每小题2分)
11.
12. 110
13. <
14. 2或1
15.24
16.菱形
17.
18.
三.计算(本题共20分,第19题12分,第20题8分)
19.计算:
(1) (2)
解:原式=1218 …… 2分 解:原式= ……2分
=6 …… 4分 = …… 4分
(3)
解:原式=
= …… 2分
=
=x1 …… 4分
20.解关于x的方程
(1); (2)(其中k为常数).
解: 解:
…… 2分 …… 1分
当k>1时,;
∴ …… 4分 当k=1时,;
当k<1时,原方程无实根. …… 4分
四.解答题(本题共22分,第21,22题6分,第23,24题每题5分)
21 .在□ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
证明:在□ABCD中
AD∥BC,AO=CO,BO=DO
∴∠GAO=∠HCO
在△AGO和△CHO中
∠GAO=∠HCO
AO=CO
∠GOA=∠HOC
∴△AGO≌△CHO
∴GO=HO …… 3分
又∵BO=DO,BE=DF
∴EO=FO
∴四边形EHFG为平行四边形 …… 6分
22.甲乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时.问二人每小时各走几千米?
解:设乙每小时走x千米,则甲每小时走(x+1)千米
根据题意,列方程得 ………… 3分
整理得
解这个方程得 ………… 5分
经检验,都是原方程的根.但速度为负数不合题意
所以只取,此时
答:甲每小时走6千米,乙每小时走5千米. ……… 6分
23.已知反比例函数的图象过点A(),过点A作AB⊥x轴于点B,且△AOB的面积为
(1) 求k和m的值;
解:∵△AOB的面积为
∴
∴
∵k<0
∴k= …… 1分
∵A()在双曲线上
∴
∴m=2 …… 2分
(2) 若一次函数的图象经过点A,并且与x轴相交于点C,求的值;
解:∵一次函数的图象经过点A()
∴ 解得
∴可求C点坐标为() …… 3分
∴AO=,AC=4 …… 4分
∴AO:AC= …… 5分
24.在下面所给的图形中,若连接BC,则四边形ABCD是矩形,四边形CBEF是平行四边形.用铅笔和
三角板画图:
(1)在图1中画出两条线段,将整个图形分成面积相等的两个部分(不写画法);
(2)在图2中画出一条线段,还能够将整个图形分成面积相等的两个部分,并写出画法的主要步骤.
解:(1)如图1或 图2 ………… 2分
(2)如图3 ………… 4分
过矩形ABCD的中心O1和平行四边形CBEF的中心O2画线段MN,交AD于M,交EF于N,则线段MN为所求. ………… 5分
五.解答题(本题共12分,第25、26题每题6分)
25. 有一块直角三角形纸片, 两直角边AC = 6cm, BC = 8cm,
①如图1,现将纸片沿直线AD折叠, 使直角边AC落在斜边AB上, 且与AB重合, 则CD = ____3_____. ……… 2分
(图1) (图2)
② 如图2,若将直角∠C沿MN折叠, 使点C落在AB中点H上, 点M、N分别在AC、BC上, 则、与之间有怎样的数量关系?并证明你的结论。
答:+=……… 3分
证明:过点B作BP∥AC交MH延长线于点P,
∴∠A=∠PBH
在△AMH和△BPH中
∠A=∠PBH
AH=BH
∠AHM=∠BHP
∴△AMH≌△BPH
∴AM=BP,MH=PH
又∵NH⊥MP
∴MN=NP
∵BP∥AC,∠C=90
∴∠NBP=90
∴
∴+=……… 6分
26. 如图1,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF.
(1)若四边形ABCD为正方形,当∠EAF=45°时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
(2)如图2,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明.
(3)在(2)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).
图1 图2
解:(1)EF=DF-BE. ………… 1分
(2)EF=DF-BE. ………… 2分
证明:在DF上截取DM=BE,连接AM.如图,
∵∠D+∠ABC=∠ABE+∠ABC=180°,
∴∠D=∠ABE.
∵AD=AB,
∴△ADM≌△ABE.
∴AM=AE,∠DAM=∠BAE.
∵∠EAF=∠BAE+∠BAF=∠BAD,
∴∠DAM+∠BAF=∠BAD.
∴∠MAF=∠BAD.
∴∠EAF=∠MAF.
∵AF是△EAF与△MAF的公共边,
∴△EAF≌△MAF.
∴EF=MF.
∵MF=DF-DM=DF-BE,
∴EF=DF-BE. ……… 4分
(3) △CEF的周长为15. ……… 6分
A
D
E
C
B
l1
l2
y
x
y
O
A
B
C
A
C
B
D
x
y
O
A
B
C
A
C
B
D
数 学 试 卷
(考试时间为100分钟,试卷满分为100分)
班级 学号 姓名 分数
一.选择题(本题共30分,每小题3分)
1.对于函数,若时,,则这个函数的解析式是( )
A. B. C. D.
2.下列各式中,运算正确的是( )
A. B.
C. ( http: / / www. / ) D.
3.下列说法中正确的是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相垂直且相等的四边形是正方形
D.两条对角线互相平分的四边形是平行四边形
4. 图象上有两点A(x1,y1)和 B(x2,y2),若y1
5. 如图,□ABCD中,∠DAB的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
A.1 B.1.5 C.2 D.3
6. 若一个等腰梯形的周长为30cm,腰长为6cm, 则它的中位线长为( )
A. 12cm B. 6cm C. 18cm D. 9cm
7.下列三角形中,不是直角三角形的是( )
A.三个内角之比为5∶6∶1 B. 一边上的中线等于这一边的一半
C.三边之长为20、21、29 D. 三边之比为1.5 : 2 : 3
8.如图,数轴上点A所表示的数为a,则a的值是( )
A.-1 B.-+1 C.+1 D.
9.如图,菱形ABCD中,E、F分别是AB、AC的中点,
若EF=3,则菱形ABCD的周长是( )
A.12 B.16
C.20 D.24
10.如图,矩形AOBC中,点A的坐标为(0,8),点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
30 B.32 C.34 D.16
二.填空题(本题共16分,每小题2分)
11.函数y =中自变量x的取值范围是_______.
12.在□ABCD中,∠A=70°,∠D=________ .
13. 比较大小: .
14.若是关于的方程的一个根,则_______.
15.矩形的两条对角线所夹的锐角为60,较短的边长为12,则对角线长为_______.
16.顺次连接等腰梯形各边中点得到的四边形是_________________.
17.如图,如果曲线l1是反比例函数在第一象限内的图象,且过点A (2,1), 那么与l1关于x轴对称的曲线l2的解析式为 (x>0).
18.如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边做垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为__________.
三.计算(本题共20分,第19题12分,第20题8分)
19.计算:
(1) (2)
解:原式= 解:原式=
(3)
解:原式=
20.解关于x的方程
(1); (2)(其中k为常数).
解: 解:
四.解答题(本题共22分,第21,22题6分,第23,24题每题5分)
21. 在□ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
22.甲乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时.问二人每小时各走几千米?
23.已知反比例函数的图象过点A(),过点A作AB⊥x轴于点B,且△AOB的面积为
(1) 求k和m的值;
(2) 若一次函数的图象经过点A,并且与x轴相交于点C,求的值;
24.在下面所给的图形中,若连接BC,则四边形ABCD是矩形,四边形CBEF是平行四边形.用铅笔和三角板画图:
(1)在图1中画出两条线段,将整个图形分成面积相等的两个部分(不写画法);
(2)在图2中画出一条线段,还能够将整个图形分成面积相等的两个部分,并写出画法的主要步骤.
五.解答题(本题共12分,第25、26题每题6分)
25. 有一块直角三角形纸片, 两直角边AC = 6cm, BC = 8cm,
①如图1,现将纸片沿直线AD折叠, 使直角边AC落在斜边AB上, 且与AB重合, 则CD = _________.
图1 图2
② 如图2,若将直角∠C沿MN折叠, 使点C落在AB中点H上, 点M、N分别在AC、BC上, 则、与之间有怎样的数量关系?并证明你的结论。
26. 如图1,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF.
(1)若四边形ABCD为正方形,当∠EAF=45°时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
(2)如图2,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明.
(3)在(2)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).
图1 图2
数 学 试 卷 参 考 答 案
一.选择题(本题共30分,每小题3分)
1 2 3 4 5 6 7 8 9 10
C C D A C D D A D A
二.填空题(本题共16分,每小题2分)
11.
12. 110
13. <
14. 2或1
15.24
16.菱形
17.
18.
三.计算(本题共20分,第19题12分,第20题8分)
19.计算:
(1) (2)
解:原式=1218 …… 2分 解:原式= ……2分
=6 …… 4分 = …… 4分
(3)
解:原式=
= …… 2分
=
=x1 …… 4分
20.解关于x的方程
(1); (2)(其中k为常数).
解: 解:
…… 2分 …… 1分
当k>1时,;
∴ …… 4分 当k=1时,;
当k<1时,原方程无实根. …… 4分
四.解答题(本题共22分,第21,22题6分,第23,24题每题5分)
21 .在□ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
证明:在□ABCD中
AD∥BC,AO=CO,BO=DO
∴∠GAO=∠HCO
在△AGO和△CHO中
∠GAO=∠HCO
AO=CO
∠GOA=∠HOC
∴△AGO≌△CHO
∴GO=HO …… 3分
又∵BO=DO,BE=DF
∴EO=FO
∴四边形EHFG为平行四边形 …… 6分
22.甲乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时.问二人每小时各走几千米?
解:设乙每小时走x千米,则甲每小时走(x+1)千米
根据题意,列方程得 ………… 3分
整理得
解这个方程得 ………… 5分
经检验,都是原方程的根.但速度为负数不合题意
所以只取,此时
答:甲每小时走6千米,乙每小时走5千米. ……… 6分
23.已知反比例函数的图象过点A(),过点A作AB⊥x轴于点B,且△AOB的面积为
(1) 求k和m的值;
解:∵△AOB的面积为
∴
∴
∵k<0
∴k= …… 1分
∵A()在双曲线上
∴
∴m=2 …… 2分
(2) 若一次函数的图象经过点A,并且与x轴相交于点C,求的值;
解:∵一次函数的图象经过点A()
∴ 解得
∴可求C点坐标为() …… 3分
∴AO=,AC=4 …… 4分
∴AO:AC= …… 5分
24.在下面所给的图形中,若连接BC,则四边形ABCD是矩形,四边形CBEF是平行四边形.用铅笔和
三角板画图:
(1)在图1中画出两条线段,将整个图形分成面积相等的两个部分(不写画法);
(2)在图2中画出一条线段,还能够将整个图形分成面积相等的两个部分,并写出画法的主要步骤.
解:(1)如图1或 图2 ………… 2分
(2)如图3 ………… 4分
过矩形ABCD的中心O1和平行四边形CBEF的中心O2画线段MN,交AD于M,交EF于N,则线段MN为所求. ………… 5分
五.解答题(本题共12分,第25、26题每题6分)
25. 有一块直角三角形纸片, 两直角边AC = 6cm, BC = 8cm,
①如图1,现将纸片沿直线AD折叠, 使直角边AC落在斜边AB上, 且与AB重合, 则CD = ____3_____. ……… 2分
(图1) (图2)
② 如图2,若将直角∠C沿MN折叠, 使点C落在AB中点H上, 点M、N分别在AC、BC上, 则、与之间有怎样的数量关系?并证明你的结论。
答:+=……… 3分
证明:过点B作BP∥AC交MH延长线于点P,
∴∠A=∠PBH
在△AMH和△BPH中
∠A=∠PBH
AH=BH
∠AHM=∠BHP
∴△AMH≌△BPH
∴AM=BP,MH=PH
又∵NH⊥MP
∴MN=NP
∵BP∥AC,∠C=90
∴∠NBP=90
∴
∴+=……… 6分
26. 如图1,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF.
(1)若四边形ABCD为正方形,当∠EAF=45°时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
(2)如图2,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明.
(3)在(2)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).
图1 图2
解:(1)EF=DF-BE. ………… 1分
(2)EF=DF-BE. ………… 2分
证明:在DF上截取DM=BE,连接AM.如图,
∵∠D+∠ABC=∠ABE+∠ABC=180°,
∴∠D=∠ABE.
∵AD=AB,
∴△ADM≌△ABE.
∴AM=AE,∠DAM=∠BAE.
∵∠EAF=∠BAE+∠BAF=∠BAD,
∴∠DAM+∠BAF=∠BAD.
∴∠MAF=∠BAD.
∴∠EAF=∠MAF.
∵AF是△EAF与△MAF的公共边,
∴△EAF≌△MAF.
∴EF=MF.
∵MF=DF-DM=DF-BE,
∴EF=DF-BE. ……… 4分
(3) △CEF的周长为15. ……… 6分
A
D
E
C
B
l1
l2
y
x
y
O
A
B
C
A
C
B
D
x
y
O
A
B
C
A
C
B
D
同课章节目录
